IBPhysicsDPSLRevision NotesInquiry ProcessInquiry 2: Collecting and Processing Data in PhysicsInterpreting results in Physics

Interpreting results in Physics (DP IB Physics): Revision Note

Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on

DP Physics: SLDP Physics: HL

Interpreting results in Physics

  • This is the "sense-making" phase of your investigation, where you analyse your processed data to find patterns, trends, and relationships

  • The primary goal is to determine what your results are telling you so that you can answer your research question

  • This almost always involves creating a graph to visualise the relationship between your independent and dependent variables

Principles of interpretation

Interpret qualitative and quantitative data

  • Your qualitative observations are crucial evidence to help explain your quantitative results.

  • For example:

    • Your calculated value for the resistivity of a wire is higher than the accepted data booklet value

    • Your qualitative observation that "the wire felt warm to the touch after several measurements" is the perfect piece of evidence to explain why

    • The heating effect of the current increased the temperature of the wire, which in turn increased its resistance, leading to a higher calculated resistivity

Interpret diagrams, graphs and charts

  • Once a line of best fit is drawn, the following features of the graph may provide important information:

    • The gradient (slope):

      • This can represent a key physical quantity

      • For a graph of I vs. V for an ohmic resistor, the gradient is the reciprocal of the resistance 1 over R

    • The y-intercept:

      • This shows the value of the dependent variable when the independent variable is zero

      • It can often reveal systematic errors, like a zero error on a sensor

    • The area under the curve:

      • This can represent a total quantity, such as the displacement from a velocity-time graph or the work done from a force-distance graph

    • Error bars:

      • The size of your error bars gives a visual representation of the precision of your data

      • Large error bars suggest significant random error

      • If the line of best fit passes through the error bars of all points, it indicates a good fit

  • Once you have your graph, you must interpret it

  • This is a two-step process:

    1. Describe the trend:

      • State what the graph shows

      • Use key scientific terms like:

        • directly proportional

        • linear positive correlation

        • inversely proportional

        • exponential increase

    2. Explain the trend:

      • You must use your knowledge of physical principles and equations to explain why the data follows this trend

      • This is the most important part of the interpretation

Identify and justify anomalous results

  • An anomalous result, or outlier, is a data point that clearly does not fit the overall trend

  • You should highlight obvious anomalous results on your final graph

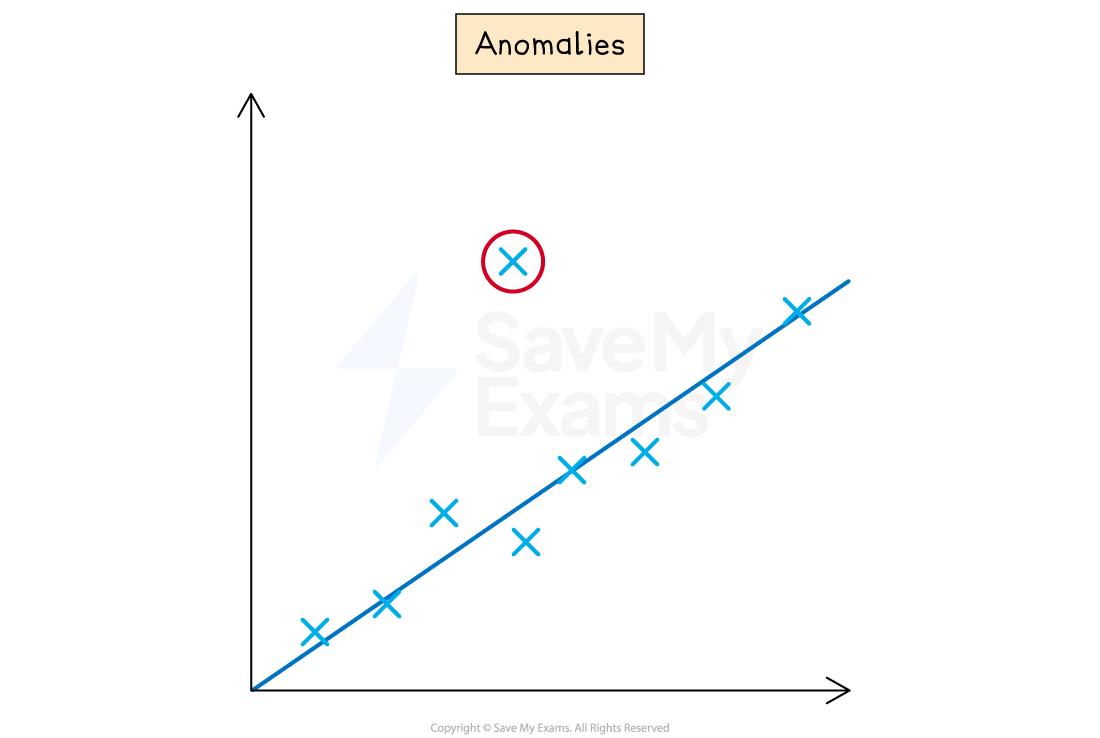
Graph showing a line of best fit with multiple points, and one point circled in red labelled as an anomaly.
Highlighting an anomalous result on a graph.

  • In your analysis, you must justify why it is an anomalous result

    • A good justification links the anomalous result to a likely experimental error

    • For example:

      • The result from trial 2 at 60°C was excluded from the average and the graph as it was significantly higher than the other two trials

      • This was likely caused by a random error, such as a delay in starting the stopwatch

Assess accuracy, precision, reliability and validity

  • These terms have very specific scientific meanings

    • Using them correctly in your interpretation shows a high level of understanding

  • Accuracy:

    • How close your final result is to the accepted or true value

    • You can only comment on accuracy if a literature value is available for comparison

    • Accuracy can be increased by repeating measurements and calculating an average

    • Repeating measurements also helps to identify anomalies that can be omitted from the final results

    • Accuracy is affected by systematic errors

      • If the systematic error in a measurement is small, then that measurement can be said to be accurate

  • Precision:

    • How close your repeat measurements are to each other

    • If a measurement is repeated several times, it can be described as precise when the values are very similar to, or the same as, each other

    • A small spread in your data indicates high precision

    • Precision is affected by random errors

      • If the random error in a measurement is small, then that measurement can be said to be precise

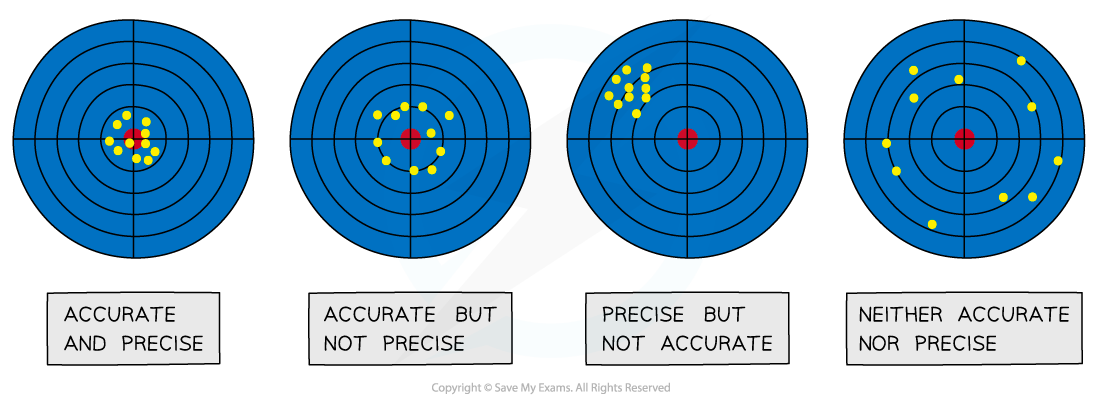
Four targets show accuracy and precision: accurate and precise, accurate not precise, precise not accurate, neither accurate nor precise.
The difference between precise and accurate results.

  • Reliability:

    • This refers to the consistency of your results

    • A reliable experiment is one which produces consistent results when repeated many times

    • Similarly, a reliable measurement is one which can be reproduced consistently when measured repeatedly 

    • When thinking about the reliability of an experiment, a good question to ask is

      • Would similar conclusions be reached if someone repeated this experiment?

  • Validity:

    • This relates to your experimental method and the appropriate choice of variables

    • Your results are valid if your experiment was a fair test, meaning you successfully controlled all other significant variables

    • Any variables that may affect the outcome of an experiment must be identified and controlled in order for the results to be valid

    • For example, when using Charles’ law to determine absolute zero, pressure must be kept constant

    • When thinking about the validity of an experiment, a good question to ask is

      • How relevant is this experiment to my original research question?

Worked Example

Research question:

  • "What is the relationship between the length of a simple pendulum and its period of oscillation?"

Graph:

  • After processing the data, a graph of square of the period T squared / s2 (y-axis) against length L / m (x-axis) is plotted

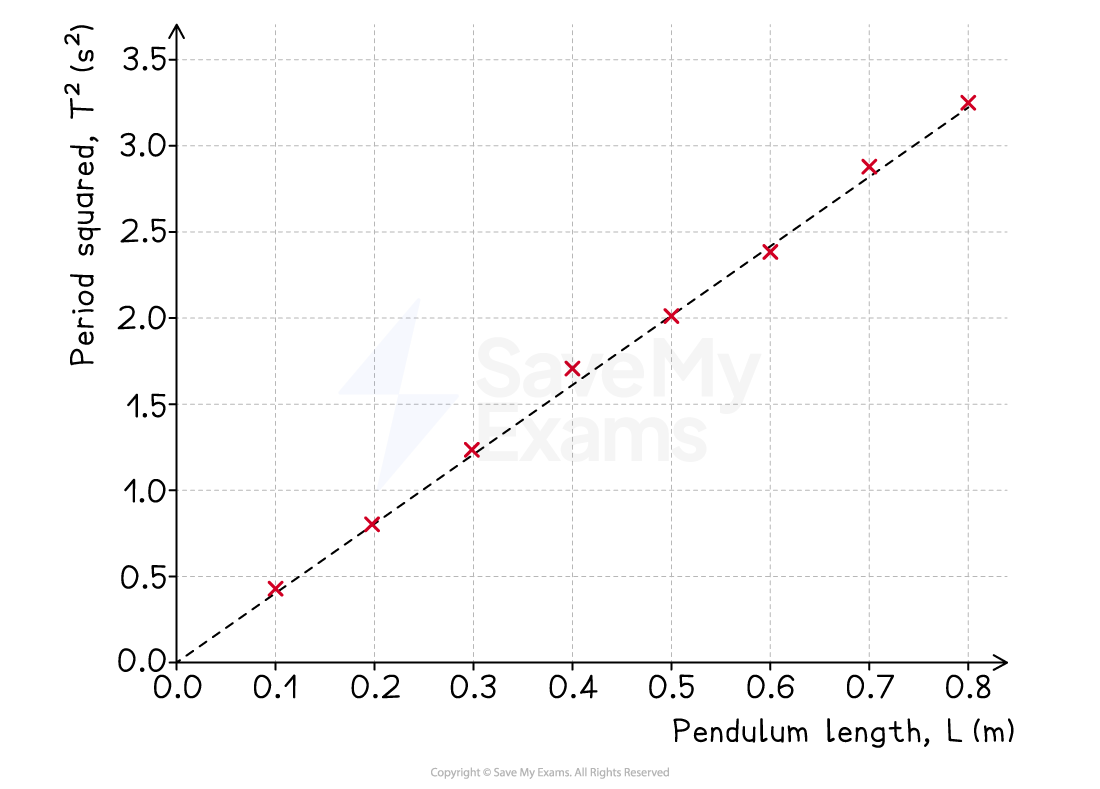
Graph of period squared (T²) versus pendulum length (L) showing a linear trend with red data points and a dashed best-fit line.

Interpretation:

  • Description of trend:

    • The graph of T squared vs. L shows a clear positive linear correlation

    • The line of best fit is a straight line that passes through the origin, which indicates that T squared is directly proportional to L

  • Explanation of trend:

    • This result is consistent with the theoretical pendulum equation, T space equals space 2 straight pi square root of L over g end root, which when rearranged, gives T squared space equals space open parentheses fraction numerator 4 straight pi squared over denominator g end fraction close parentheses L

    • This equation is in the form y space equals space m x, confirming the directly proportional relationship between T squared and L

  • Using the gradient:

    • The gradient of the graph was calculated to be 4.05 s2 m-1

    • Using the relationship gradient = fraction numerator 4 straight pi squared over denominator g end fraction , the experimental value for the acceleration due to gravity was found to be g space equals space fraction numerator 4 straight pi squared over denominator 4.05 end fraction = 9.76 m s-2

    • This is very close to the accepted value of 9.81 m s-2, with a percentage error of only 0.5%, suggesting the data is highly accurate

Worked Example

Research question:

  • "What is the relationship between the length of a constantan wire and its electrical resistance?"

Graph:

  • After processing the data, a graph of resistance R / Ω (y-axis) against length L / m (x-axis) is plotted

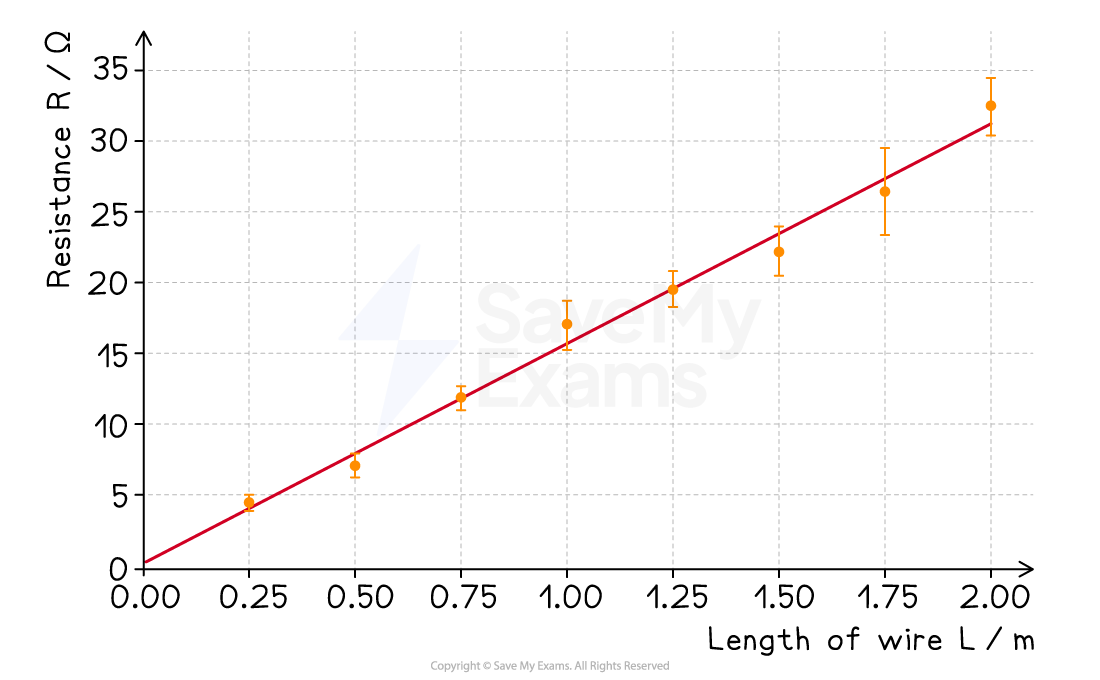
Graph showing the linear relationship between wire length in metres and resistance in ohms, plotted with data points and a red trend line.

Processed data:

  • The average diameter of the wire was calculated as 0.19 mm

Interpretation:

  • Precision and reliability:

    • The error bars for the resistance values are small, indicating that the measurements of voltage and current were precise

    • The data points all lie very close to the line of best fit, suggesting the relationship is strong and the results are reliable

  • Accuracy:

    • The y-intercept of the graph is +0.25 Ω

      • Theoretically, a wire of zero length should have zero resistance, so the line should pass through the origin

      • This non-zero intercept suggests the presence of a small systematic error, such as contact resistance from the crocodile clips, which adds a small amount of extra resistance to all measurements

    • The gradient of the graph is 15.54 Ω m-1

      • Using the relationship rho space equals space gradient space cross times space Awith A space equals space straight pi r squared = 2.84 × 10-8 m2, the experimental value for the resistivity of constantan wire was found to be rho = 4.41 × 10-7 Ω m

      • A literature search shows that the resistivity of constantan wire is 4.94 × 10-7 Ω m

      • The result is very close to the accepted value, suggesting that the result is accurate

Examiner Tips and Tricks

Explain the physics.

  • The most important part of your interpretation is linking the trend in your graph back to the relevant physical theory and equations.

  • This moves your analysis from a simple description to a scientific explanation.

Stay focused on your research question.

  • Remember: the ultimate goal of interpreting results is to test your hypothesis and answer your research question.

  • Keep circling back to this in your analysis.

Highlight anomalies transparently.

  • Never delete data without comment.

  • Mark and explain anomalous points, and use physics reasoning (not just “it looks odd”) to justify your decision.

Use the key vocabulary.

  • Explicitly use the terms accuracy, precision, and reliability in your interpretation.

  • This clearly demonstrates to the examiner that you understand the quality of your results.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Processing data in PhysicsNext:Concluding in Physics
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Reviewer: Caroline Carroll

    Expertise: Physics & Chemistry Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.