Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)SLRevision Notes3. Geometry & TrigonometryTrigonometric Functions & GraphsTransformations of Trigonometric Functions

Transformations of Trigonometric Functions (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

DP Analysis & Approaches (AA): SLDP Analysis & Approaches (AA): HL

Transformations of trigonometric functions

How do I apply a single transformation to a trig graph?

  • You can transform a trig graph using

    • a translation

    • a stretch

    • a reflection

  • The table below shows the equations of the trig graphs after each transformation

Transformation

Equation

Details

Horizontal translation

y equals tan open parentheses x plus k close parentheses

  • To the right if k is negative

  • To the left if k is positive

Vertical translation

y equals tan open parentheses x close parentheses plus k

  • Up if k is positive

  • Down if k is negative

Horizontal stretch

y equals sin open parentheses k x close parentheses

Scale factor 1 over k

Vertical stretch

y equals k sin open parentheses x close parentheses

Scale factor k

Reflection in the y-axis

y equals cos open parentheses negative x close parentheses

Reflection in the x-axis

y equals negative cos open parentheses x close parentheses

How do I apply multiple transformations to a trig graph?

  • You need to be able to apply multiple transformations to draw graphs written in the form

    • y equals a sin open parentheses b open parentheses x minus c close parentheses close parentheses plus d

  • The order for the vertical transformations are:

    • Reflection in the x-axis if a is negative

    • Stretch by scale factor a

    • Translation d units

      • Up if positive

      • Down if negative

  • The order for the horizontal transformations are:

    • Reflection in the y-axis if b is negative

    • Stretch by scale factor 1 over b

    • Translation c units

      • Right if it's x minus c

      • Left if it's x plus c

Examiner Tips and Tricks

It does not matter if you do the vertical transformations or the horizontal transformations first.

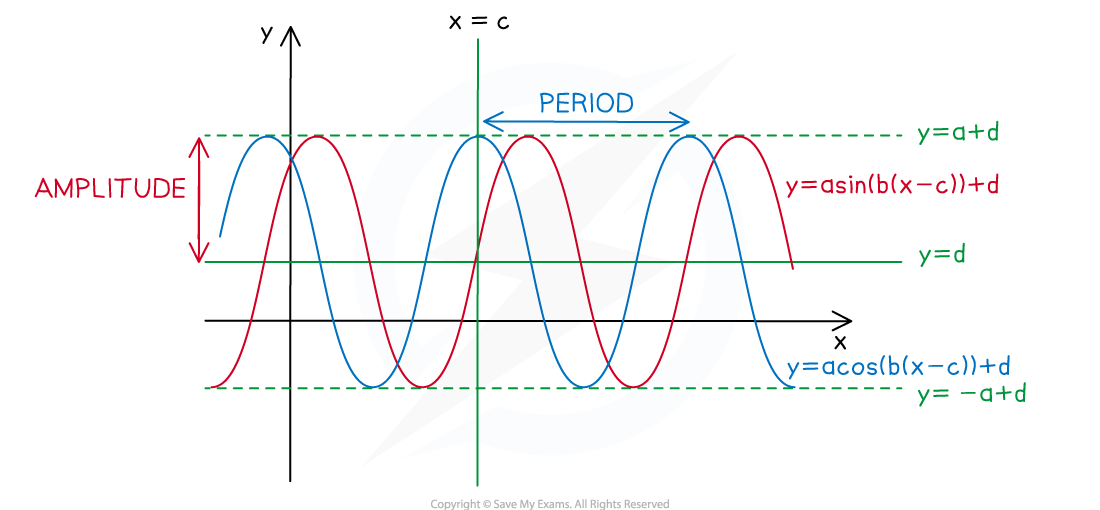
How do transformations affect the trig graph?

  • The graph y equals a sin open parentheses b open parentheses x minus c close parentheses close parentheses plus d and y equals a cos open parentheses b open parentheses x minus c close parentheses close parentheses plus d have the properties:

    • The principal axis is y equals d

    • The amplitude is open vertical bar a close vertical bar

    • The period is fraction numerator 360 degree over denominator open vertical bar b close vertical bar end fraction

    • The phase shift is b

  • You can use these properties to sketch a transformed trig graph

  • e.g. y equals 2 sin open parentheses 3 open parentheses x minus 45 degree close parentheses close parentheses minus 1

    • Draw a sine curve without any axes

    • Identify where the x-axis should go

      • Label the principal axis y equals negative 1

      • Label the maximum points at y equals negative 1 plus 2 equals 1

      • Label the minimum points at y equals negative 1 minus 2 equals negative 3

    • Find the period fraction numerator 360 degree over denominator 3 end fraction equals 120 degree

      • You can label the intersections with the principal axis temporarily as 0°, 60°, 120°, etc

    • Identify where the y-axis should go

      • Temporally put the y-axis going through 0°

      • Translate the graph 45° to the right

      • Add 45° to the intersections with the principal axis

Graph showing sine and cosine functions with amplitude and period annotations, labelled equations y=asin(b(x-c))+d and y=acos(b(x-c))+d.
Example of transformations of trig graphs

  • The graph y equals a tan open parentheses b open parentheses x minus c close parentheses close parentheses plus d works similarly

    • There is no amplitude

    • The graph has no minimum or maximum points

    • The period is fraction numerator 180 degree over denominator open vertical bar b close vertical bar end fraction

    • The graph has asymptotes

      • These are located halfway between the intersections of the graph with the principal axis

Examiner Tips and Tricks

Check your sketch is correct by substituting easy values (such as x equals 0) into the equation.

Worked Example

Sketch the graph of y blank equals 2 space sin open parentheses 3 open parentheses x blank – pi over 4 close parentheses close parentheses minus 1 for the interval negative 2 pi space less or equal than space x space less or equal than space 2 pi. State the amplitude, period and principal axis of the function.

aa-sl-3-5-2-transformations-of-trig-functions-we-solution-1

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Solving Equations Using Trigonometric GraphsNext:Modelling with Trigonometric Functions
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.