Finding Areas Using a GDC (DP IB Applications & Interpretation (AI)): Revision Note

Area Under a Curve Basics

What is meant by the area under a curve?

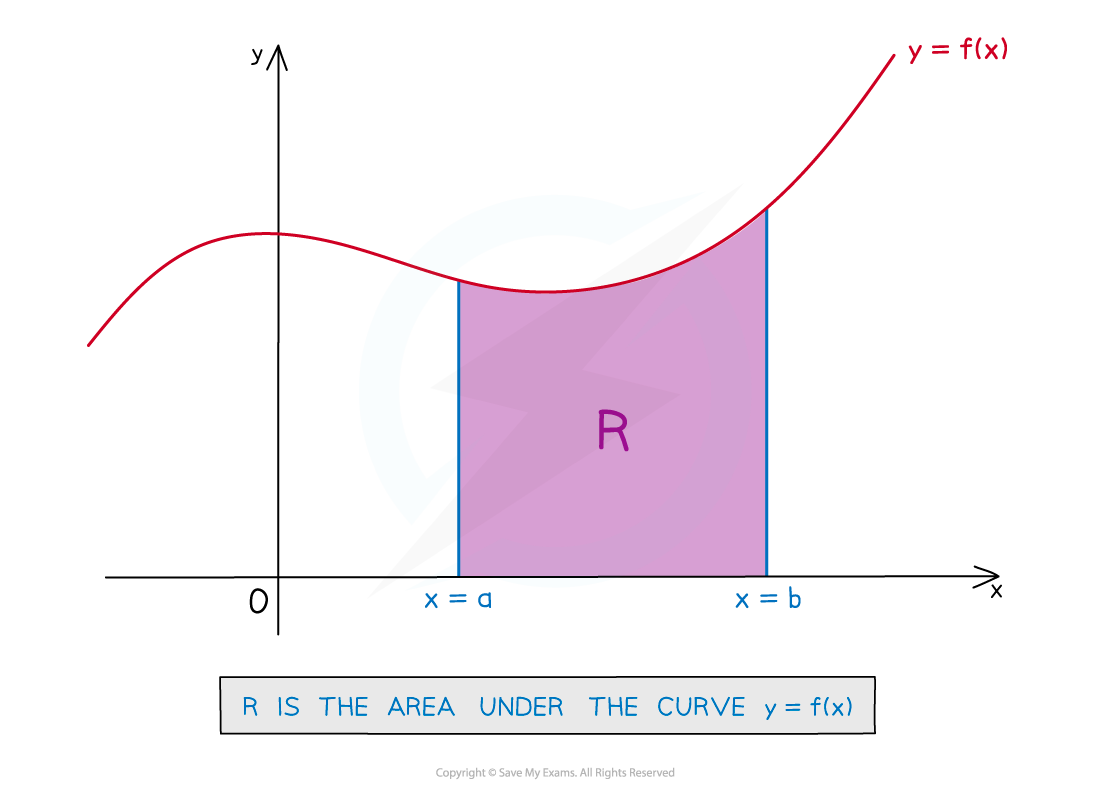
• The phrase “area under a curve” refers to the area bounded by

  • the graph of 

  • the -axis

  • the vertical line 

  • the vertical line 

• The exact area under a curve is found by evaluating a definite integral

• The graph of  could be a straight line

  • the use of integration described below would still apply

    • but the shape created would be a trapezoid

    • so it is easier to use “”

What is a definite integral?

• This is known as the Fundamental Theorem of Calculus

• a and b are called limits

  • a is the lower limit

  • b is the upper limit

•  is the integrand

•  is an antiderivative of

• The constant of integration (“”) is not needed in definite integration

  • "” would appear alongside both F(a) and F(b)

  • subtracting means the “”’s cancel

How do I form a definite integral to find the area under a curve?

• The graph of  and the -axis should be obvious boundaries for the area so the key here is in finding  and  - the lower and upper limits of the integral 

 STEP 1

Use the given sketch to help locate the limits

You may prefer to plot the graph on your GDC and find the limits from there

STEP 2

Look carefully where the ‘left’ and ‘right’ boundaries of the area lie
If the boundaries are vertical lines, the limits will come directly from their equations
Look out for the -axis being one of the (vertical) boundaries – in this case the limit () will be 0

One, or both, of the limits, could be a root of the equation

i.e.  where the graph of crosses the -axis

In this case solve the equation to find the limit(s)

A GDC will solve this equation, either from the graphing screen or the equation solver

STEP 3

The definite integral for finding the area can now be set up in the form

Definite Integrals using GDC

Does my calculator/GDC do definite integrals?

• Modern graphic calculators (and some ‘advanced’ scientific calculators) have the functionality to evaluate definite integrals

  • i.e. they can calculate the area under a curve (see above)

• If a calculator has a button for evalutaing definite integrals it will look something like

• This may be a physical button or accessed via an on-screen menu

• Some GDCs may have the ability to find the area under a curve from the graphing screen

• Be careful with any calculator/GDC, they may not produce an exact answer

How do I use my GDC to find definite integrals?

Without graphing first …

• Once you know the definite integral function your calculator will need three things in order to evaluate it

  • The function to be integrated (integrand) ()

  • The lower limit ( from )

  • The upper limit ( from )

• Have a play with the order in which your calculator expects these to be entered – some do not always work left to right as it appears on screen!

With graphing first ...

• Plot the graph of 

  • You may also wish to plot the vertical lines  and 

    • make sure your GDC is expecting an "" style equation

  • Once you have plotted the graph you need to look for an option regarding “area” or a physical button

    • it may appear as the integral symbol (e.g. )

    • your GDC may allow you to select the lower and upper limits by moving a cursor along the curve - however this may not be very accurate

    • your GDC may allow you to type the exact limits required from the keypad