GCSEFurther MathsAQARevision Notes2. Algebra & FunctionsShapes of GraphsSolving Equations using Graphs

Solving Equations using Graphs (AQA GCSE Further Maths): Revision Note

Exam code: 8365

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on 11 August 2026

Guided study available on this topic

Understand this topic with deeper explanations and understanding checks.

Solving equations using graphs

How do we use graphs to solve equations?

Solutions are always read off the x-axis
Solutions of f(x) = 0 are where the graph of y = f(x) crosses the x-axis
If asked to use the graph of y = f(x) to solve a different equation (the question will say something like “by drawing a suitable straight line”) then:
- Rearrange the equation to be solved into f(x) = mx + c and draw the line y = mx + c
- Solutions are the x-coordinates of where the line (y = mx + c) crosses the curve (y = f(x))
- E.g. if given the curve for y = x³ + 2x²+ 1 and asked to solve x³ + 2x² − x − 1 = 0, then;
  1. rearrange x³ + 2x² − x − 1 = 0 to x³ + 2x²+ 1 = x + 2
  2. draw the line y = x + 2 on the curve y = x³ + 2x²+ 1
  3. read the x-values of where the line and the curve cross (in this case there would be 3 solutions, approximately x = -2.2, x = -0.6 and x = 0.8);

Note that solutions may also be called roots

Examiner Tips and Tricks

If solving an equation, give the x values only as your final answer
If solving a pair of linear simultaneous equations give an x and a y value as your final answer
If solving a pair of simultaneous equations where one is linear and one is quadratic, give two pairs of x and y values as your final answer

Worked Example

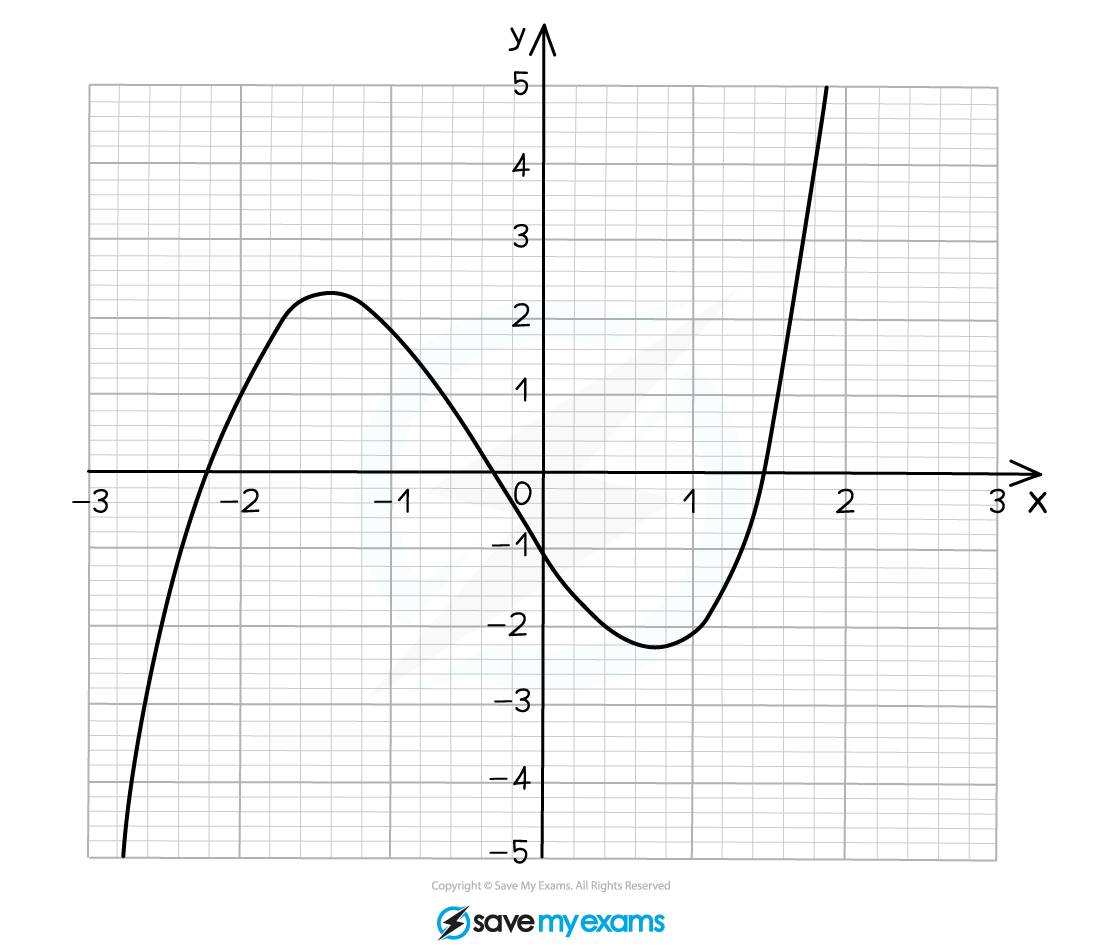
The graph of $y = x^{3} + x^{2} - 3 x - 1$ is shown below.
Use the graph to estimate the solutions of the equation $x^{3} + x^{2} - 4 x = 0$ . Give your answers to 1 decimal place.

Cubic-Linear-Intersections-(before), IGCSE & GCSE Maths revision notes

We are given a different equation to the one plotted so we must rearrange it to $f (x) = m x + c$ (where $f (x)$ is the plotted graph)

$\begin{array}{rcl} x^{3} + x^{2} - 4 x & = & 0 \end{array}$

$\begin{array}{rcl} + x - 1 + x - 1 \end{array}$

$\begin{array}{rcl} x^{3} + x^{2} - 3 x - 1 & = & x - 1 \end{array}$

Now plot $y = x - 1$ on the graph- this is the solid red line on the graph below

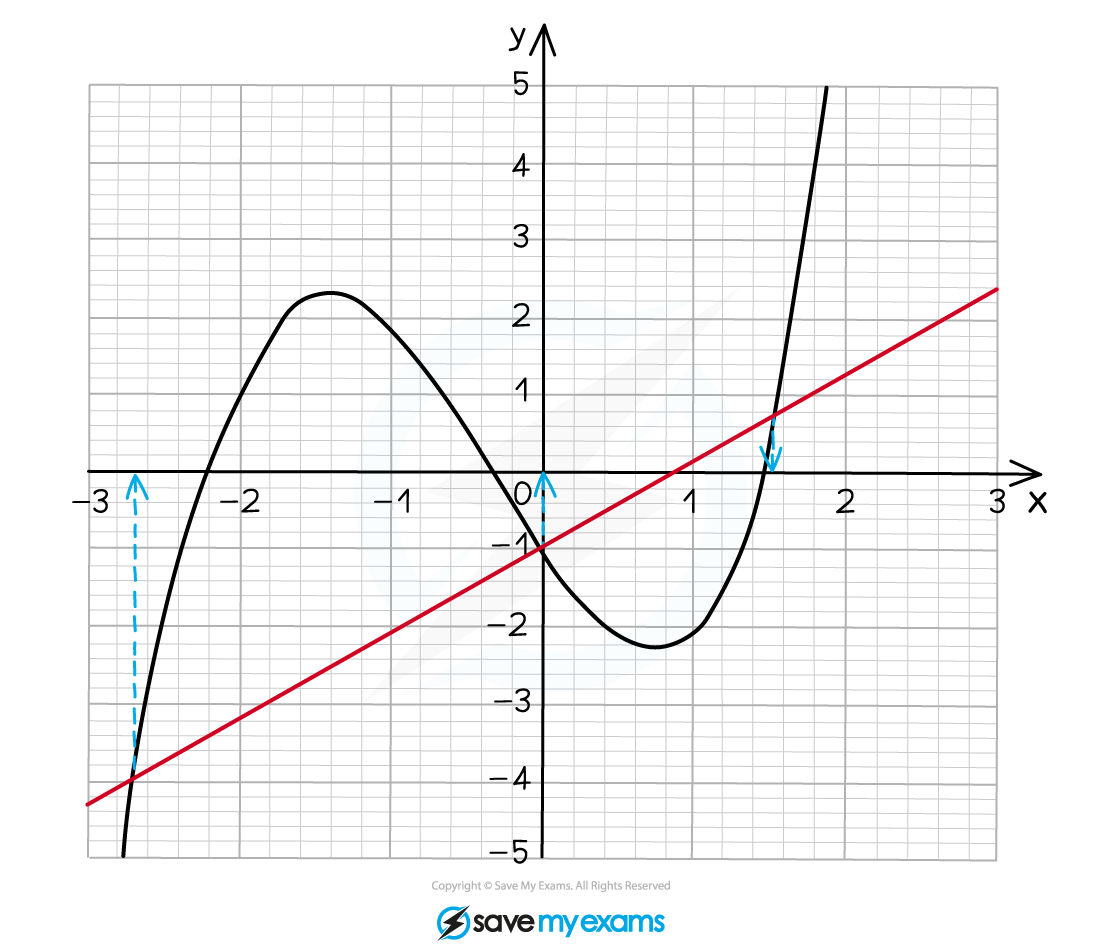
Cubic-Linear-Intersections-(after), IGCSE & GCSE Maths revision notes

The solutions are the $x$ coordinates of where the curve and the straight line cross so

$x = - 2.6, x = 0, x = 1.6$

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent