Extension & Compression (Cambridge (CIE) A Level Physics): Revision Note
Exam code: 9702
Tensile force
Forces can change the size and shape of a body, as well as their motion
When forces change the size or shape of a body this is known as deformation
Forces acting in opposite directions stretch or compress a body
When two forces stretch a body, they are described as tensile forces
When two forces compress a body, they are known as compressive forces
Tensile and compressive forces
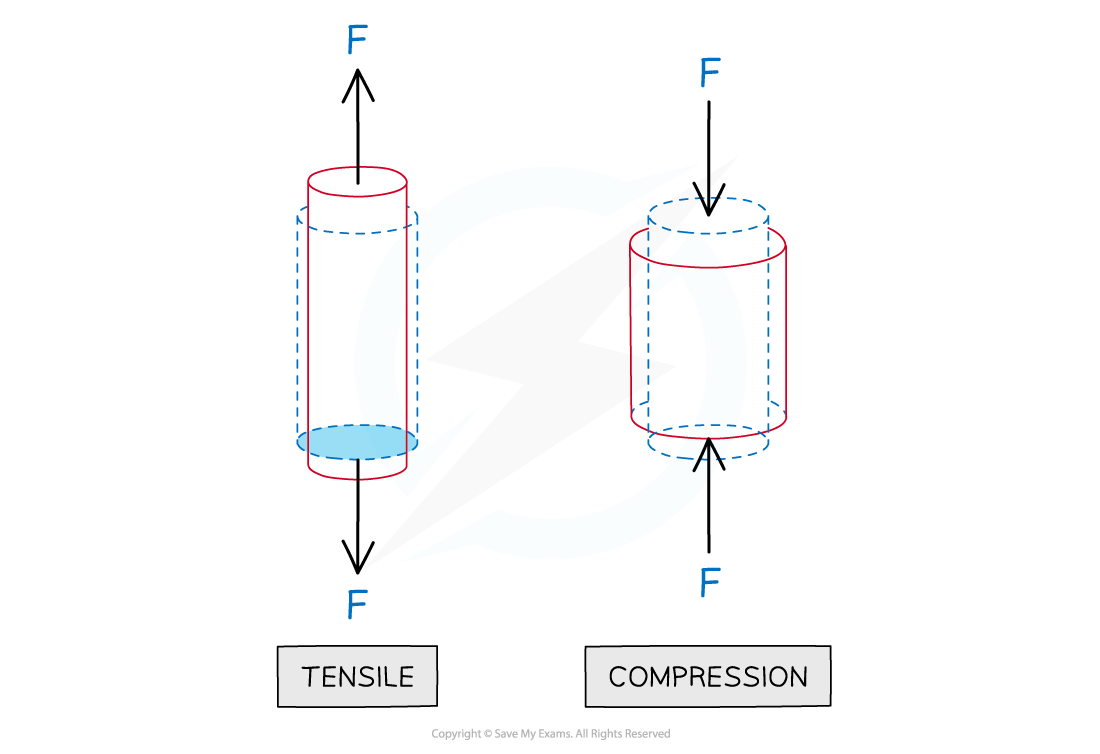
Tensile forces act to increase the length of an object, compressive forces act to reduce the length of an object in a given dimension
Extension & compression
A load attached to the end of a spring
applies a force to the spring
which causes it to extend or compress
The natural length of a spring is its length without any force applied
A spring that increases in length undergoes extension
The amount of extension can be calculated by subtracting the natural length from the extended length
A spring that decreases in length undergoes compression
The amount of compression can be calculated by subtracting the compressed length from the natural length
Tensile force on a spring
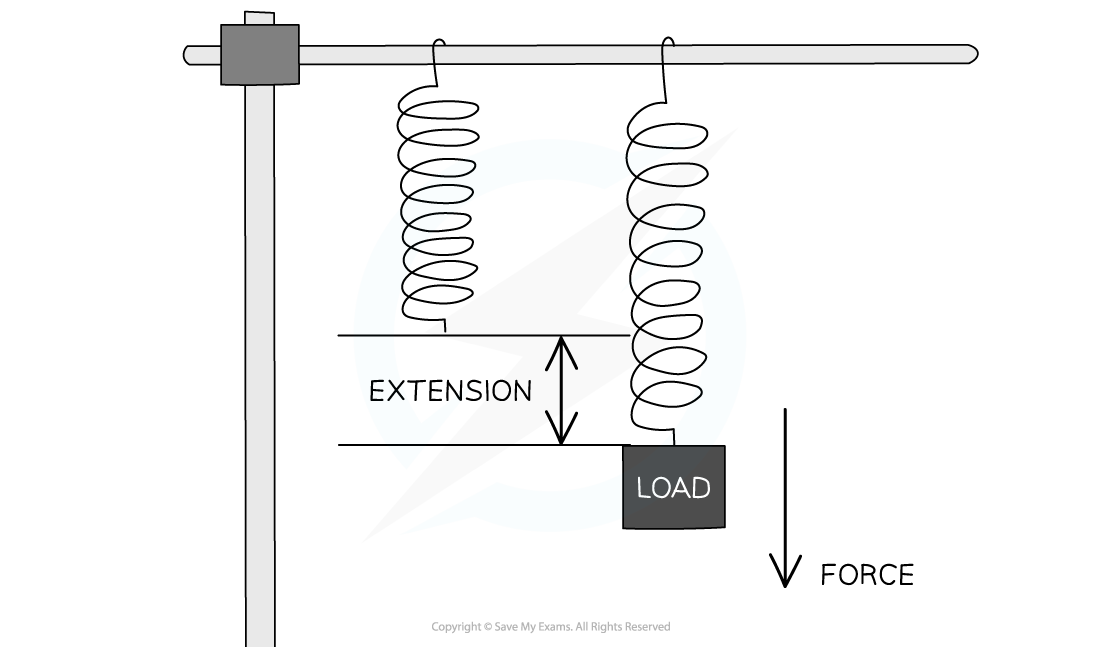
Stretching a spring with a load produces a force that leads to an extension
When a spring demonstrates elastic behaviour a load applied creates an extension that can be removed so the spring returns to its original length
This occurs until the point at which the spring reaches its limit of proportionality
When the spring exceeds the limit of proportionality, the relationship between force and extension is no longer proportional
The spring no longer obeys Hooke's law
Force–extension graphs
The way a material responds to a given force can be shown on a force-extension graph
Every material will have a unique force-extension graph depending on its properties
A force-extension graph contains a linear and then a non-linear region
The limit of proportionality is the point at which the force-extension graph changes from the linear to the non-linear region
Force-extension graph
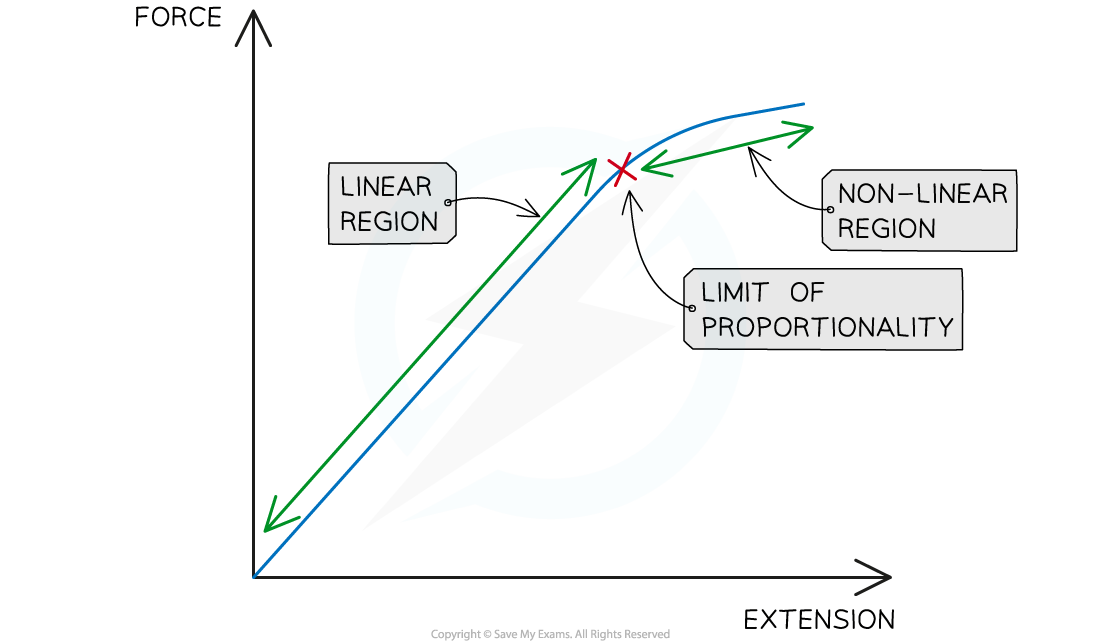
Linear and non-linear regions of a force-extension graph
Worked Example
Which graph represents the force-extension relationship of a rubber band that is stretched almost to its breaking point?
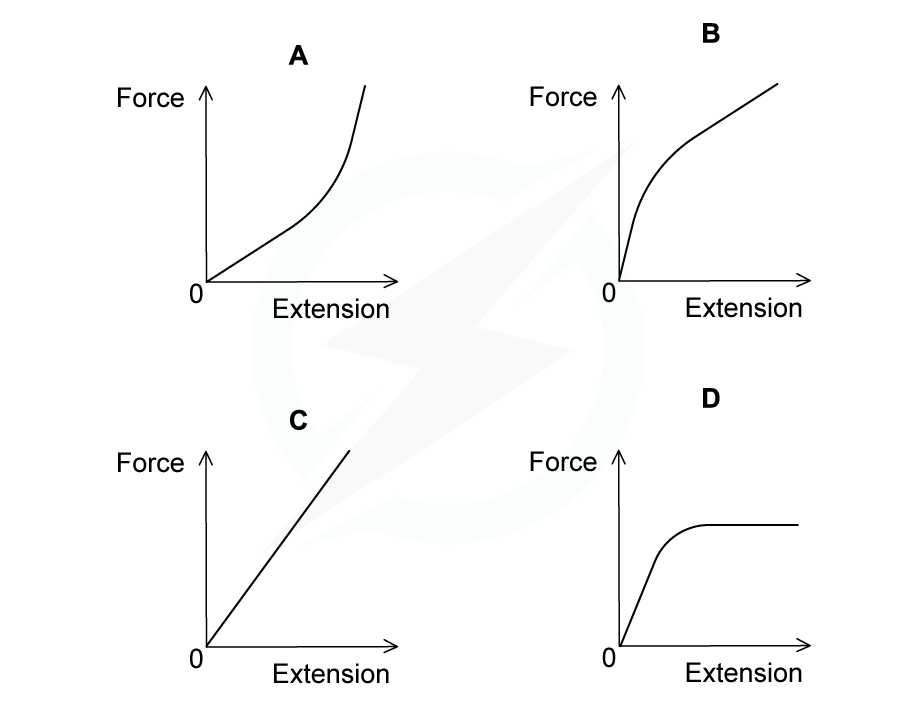
Answer: A
Rubber bands can be stretched up to twice their original size or more - this is because the long chain molecules become fully aligned and can no longer move past each other
This is shown by graph A - after the section of linear proportionality (the straight line), the gradient increases significantly, so, a large force is required to extend the rubber band by even a small amount
Graph B is incorrect as the gradient decreases, suggesting that less force is required to cause a small extension
Graph C is incorrect as this shows a material that does not break easily, such as a metal
Graph D is incorrect as the plateau suggests no extra force is required to extend the rubber as it has already been stretched
Worked Example
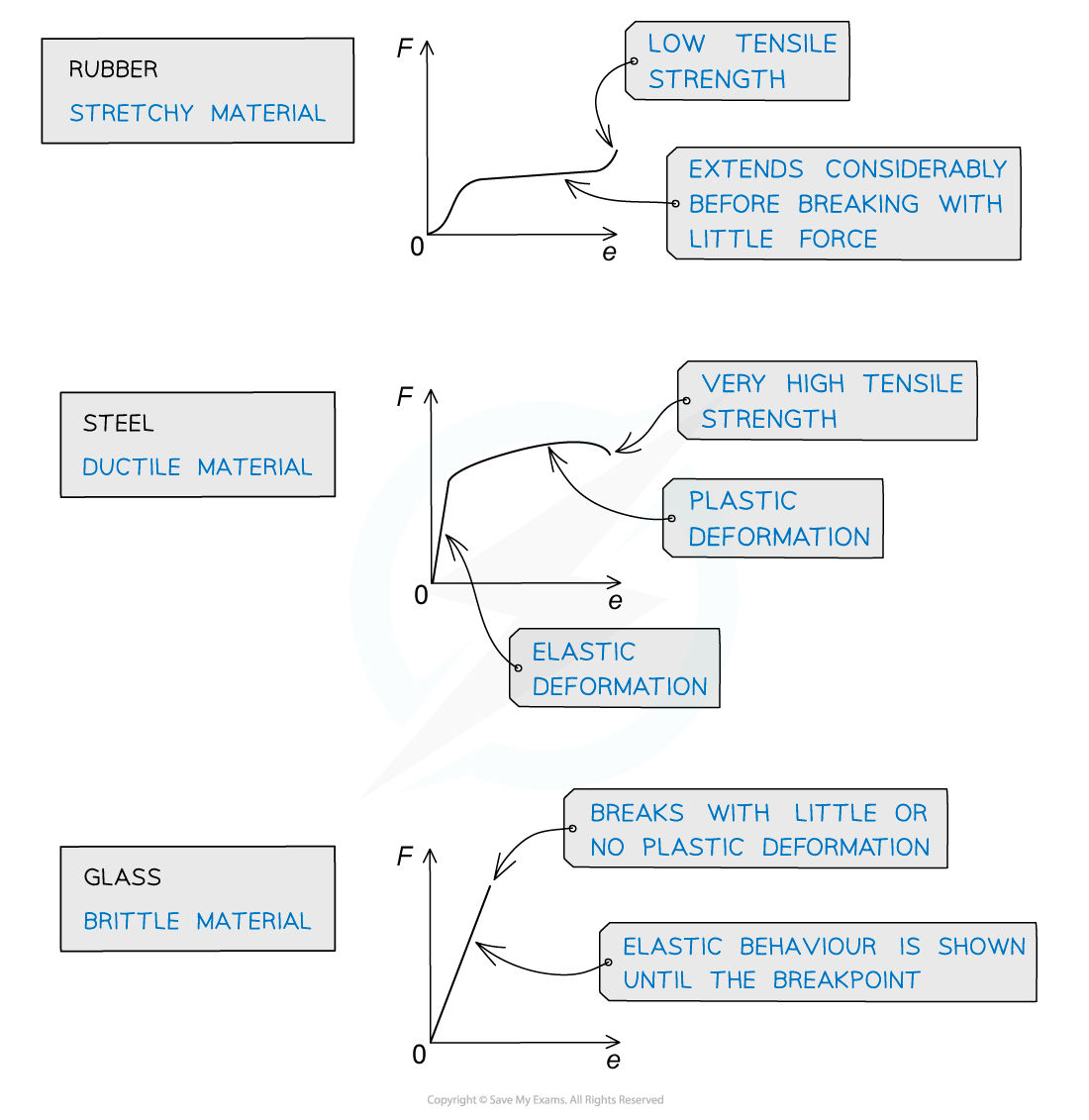
Cylindrical samples of steel, glass and rubber are each subjected to a gradually increasing tensile force F. The extensions e are measured and graphs are plotted as shown below.
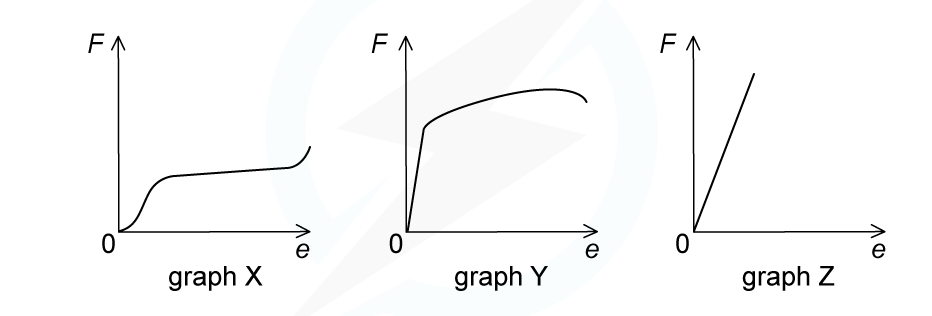
Correctly label the graphs with the materials: steel, glass, rubber.
Examiner Tips and Tricks
Exam questions may ask for the total length of a material after a load is placed on it and it has extended. Remember to add the extension to the original length of the material to get its final full length

Unlock more, it's free!
Was this revision note helpful?
