Logistic Models (DP IB Applications & Interpretation (AI)): Revision Note

Logistic functions & graphs

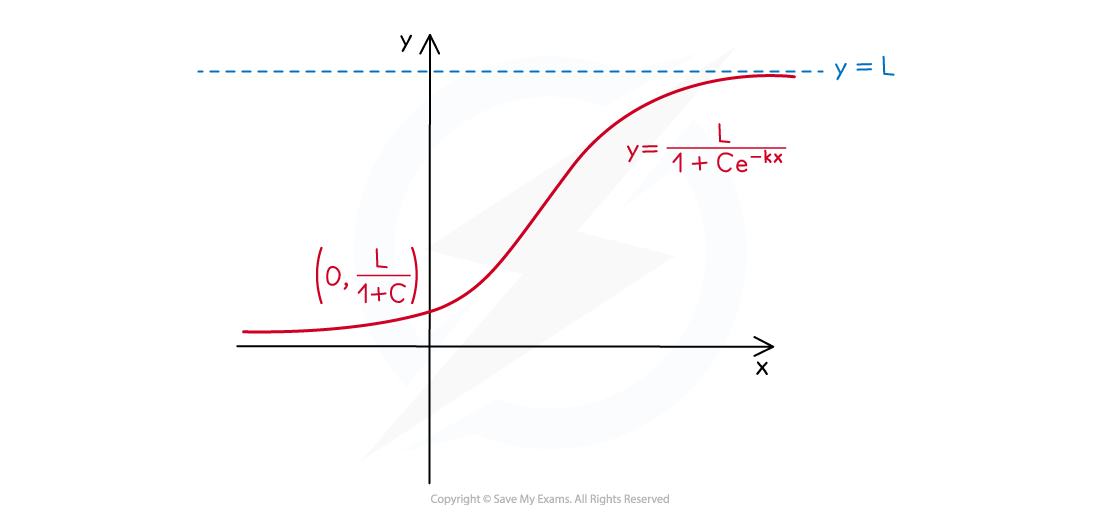
What are the key features of logistic graphs?

• A logistic function is of the form 

  • , & are positive constants

• Its domain is the set of all real values

• Its range is the set of real positive values less than

• The y-intercept is at the point 

• There are no roots

• There is a horizontal asymptote at

  • This is the upper limit of the function

    • This is called the carrying capacity

  • e.g. it could represent the limit of a population size

• There is a horizontal asymptote at

• The graph is always increasing

Logistic models

What are the parameters of logistic models?

• A logistic model is of the form 

• The value of represents the limiting capacity

  • This is the value that the model tends to as gets large

• The value of (along with the ) helps to determine the initial value of the model

  • The initial value is given by 

  • Once has been determined you can then determine

• The value of determines the rate of increase of the model

What can be modelled using a logistic model?

• A logistic model can be used when the variable initially increases exponentially and then tends towards a limit

  • H(t) is the height of a giraffe t weeks after birth

  • P(t) is the number of bacteria on an apple t seconds after removing from protective packaging

  • P(t) is the population of rabbits in a woodlands area t weeks after releasing an initial amount into the area

What are possible limitations of a logistic model?

• A logistic graph is bounded by the limit

  • However in real-life the variable might be unbounded

    • e.g. the cumulative total number of births in a town over time

• A logistic graph is always increasing

  • However, in real-life there could be periods where the variable decreased or fluctuates