Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes3. Geometry & TrigonometryGraph TheoryWalks & Adjacency Matrices

Walks & Adjacency Matrices (DP IB Applications & Interpretation (AI)): Revision Note

Naomi C

Written by: Naomi C

Reviewed by: Dan Finlay

Updated on

Walks & adjacency matrices

What is an adjacency matrix?

  • An adjacency matrix can be used to represent a graph

  • It is a square matrix where all the vertices in the graph are listed as the headings for both the rows (i) and columns (j)

  • The entry a subscript i j end subscript represents the number of edges that go from vertex i to vertex j

  • In a simple graph the only entries are either 0 or 1

  • The matrix will be symmetrical for an undirected graph

  • A loop counts as one edge

Examiner Tips and Tricks

Be careful! This is not fully agreed amongst mathematicians. Some people add 2 for every loop. This means that the sum of the entries in a row or column is equal to the degree of the vertex.

However, when counting walks it is best to consider a loop as one walk, unless you clockwise and counter-clockwise directions need to be considered separately.

  • For a directed graph

    • The sum of the entries in a row is the out degree of that vertex

    • The sum of the entries in a column is the in degree of that vertex

    • A loop always counts as 1 as there is a direction involved

  • For example, consider table row blank cell table row A B C end table end cell row cell table row A row B row C end table end cell cell open parentheses table row 1 2 1 row 0 1 2 row 3 0 0 end table close parentheses end cell end table

    • There is 1 edge that start at A and end at C

    • There are 3 edges that start at C and end at A

Worked Example

Let G be the graph below.

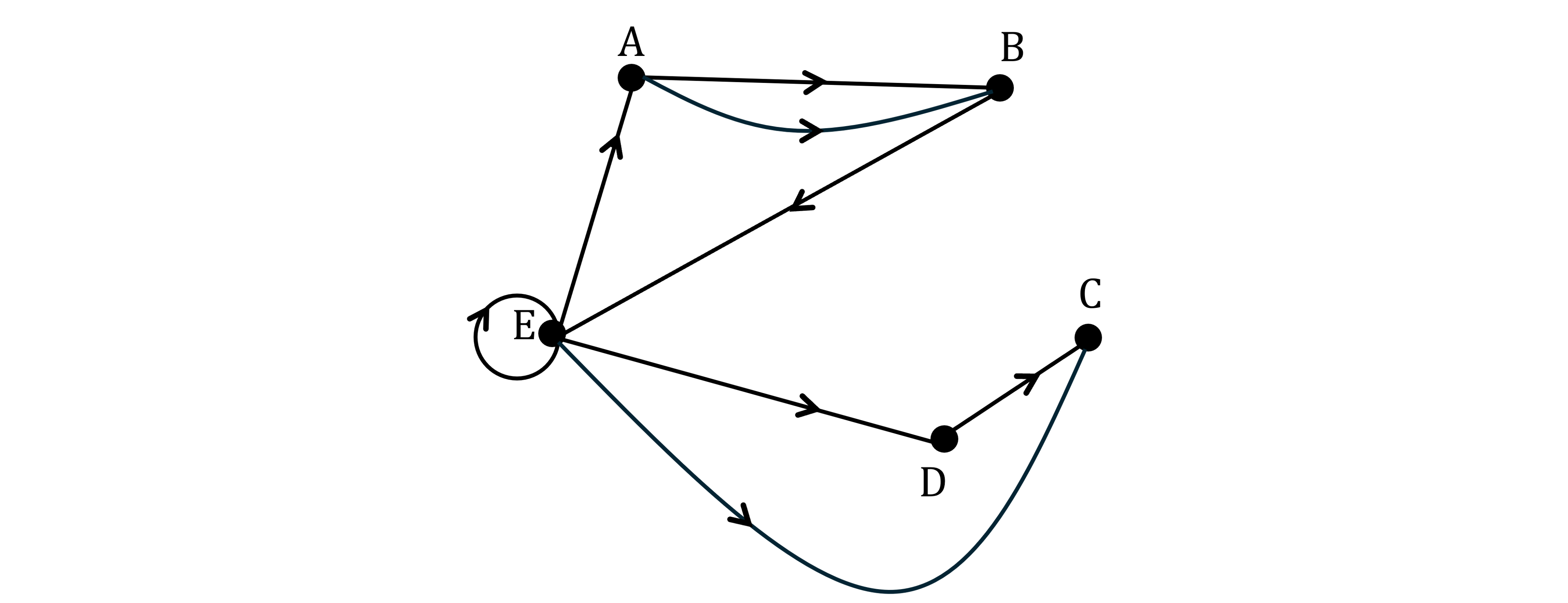
3-10-2-ib-hl-ai-walks--adjacency-matrices-we-1

Write down the adjacency matrix for G.

rn-3-10-graph-theory

Number of walks

What is the length of a walk?

  • The length of a walk is the number of edges that are traversed

How do I calculate the number of walks between a pair of vertices?

  • Let bold italic M denote the adjacency matrix of a graph

  • The entries of the adjacency matrix bold italic M tells you the number of walks of length 1 between each pair of vertices

    • The (i, j) entry in the matrix bold italic M is the number of 1-length walks from vertex i to vertex j

  • The entries of the adjacency matrix bold italic M to the power of k tells you the number of walks of length k between each pair of vertices

    • The (i, j) entry in the matrix bold italic M to the power of k is the number of k-length walks from vertex i to vertex j

Examiner Tips and Tricks

This matrix gives the number of walks that contain exactly k edges.

  • For example, if table row cell bold italic M equals open parentheses table row 1 2 1 row 0 1 2 row 3 0 0 end table close parentheses end cell end table is the adjacency matrix

    • Then bold italic M cubed equals open parentheses table row 19 12 12 row 12 13 8 row 12 12 15 end table close parentheses

      • There are 8 walks from B to C which use exactly 3 edges

  • If you need to find the total number of walks of at most length n

    • Calculate bold italic M plus bold italic M squared plus... plus bold italic M to the power of n

      • You can denote this bold italic S subscript n

    • The (i, j) entry in this matrix is the number of walks from vertex i to vertex j of length at most n

Worked Example

The adjacency matrix M of a graph G is given by

a) Draw the graph described by the adjacency matrix M.

3-10-2-ib-hl-ai-walks--adjacency-matrices-we-2a-solution

b) Find the number of walks of length 4 from vertex B to Vertex E.

3-10-2-ib-hl-ai-walks--adjacency-matrices-we-2b-solution

c) Find the number of walks of 3 or less from vertex A to vertex C.

3-10-2-ib-hl-ai-walks--adjacency-matrices-we-2c-solution

Weighted adjacency tables

What is a weighted adjacency table?

  • A weighted adjacency table is different to an adjacency matrix

    • The value in each cell is the weight of the edge connecting that pair of vertices

      • Weight could be cost, distance, time etc.

  • An empty cell can be used to indicate that there is no connection between a pair of vertices

  • Weighted adjacency tables can be used to find:

  • You can construct transition matrices when the weights represent probabilities

Worked Example

The table below shows the time taken in minutes to travel by car between 4 different towns.

 

A

B

C

D

A

 -

16

35

 -

B

16

- 

20

18

C

35

20

 -

34

D

 -

23

34

 -

State the time taken to drive from Town B to Town D.

3-10-2-ib-hl-ai-walks--adjacency-matrices-we-3b-solution

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Introduction to Graph TheoryNext:Minimum Spanning Trees (Kruskal's Algorithm)
    Author
    Reviewer
    Naomi C

    Author: Naomi C

    Expertise: Maths Content Creator

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.