IGCSEMathsEdexcelMaths BRevision NotesFunctionsGraphs of FunctionsCubic Graphs

Cubic Graphs (Edexcel IGCSE Maths B): Revision Note

Exam code: 4MB1

Roger B

Written by: Roger B

Reviewed by: Jamie Wood

Updated on

Edexcel Maths BCambridge (CIE) International Maths: Extended

Cubic Graphs

What is a cubic?

  • A cubic is a function of the form a x cubed plus b x squared plus c x plus d

    • a comma space b comma space c and d are constants

    • It is a polynomial of degree (order) 3

      • So b comma space c and/or d could be zero

      • but a cannot be zero

  • To sketch the graph of a cubic, the polynomial needs to be in factorised form

    • E.g. open parentheses 2 x minus 1 close parentheses open parentheses x plus 2 close parentheses open parentheses x minus 3 close parentheses is the factorised form of 2 x cubed minus 3 x squared minus 11 x plus 6

  • Some cubics are simple to factorise

    • E.g. x cubed minus 4 x equals x open parentheses x squared minus 4 close parentheses equals x open parentheses x minus 2 close parentheses open parentheses x plus 2 close parentheses

  • For more complicated cubics you may be able to factorise them using the factor theorem and algebraic division

  • You should also be able to expand three brackets to find the expanded form of a cubic

What does the graph of a cubic look like?

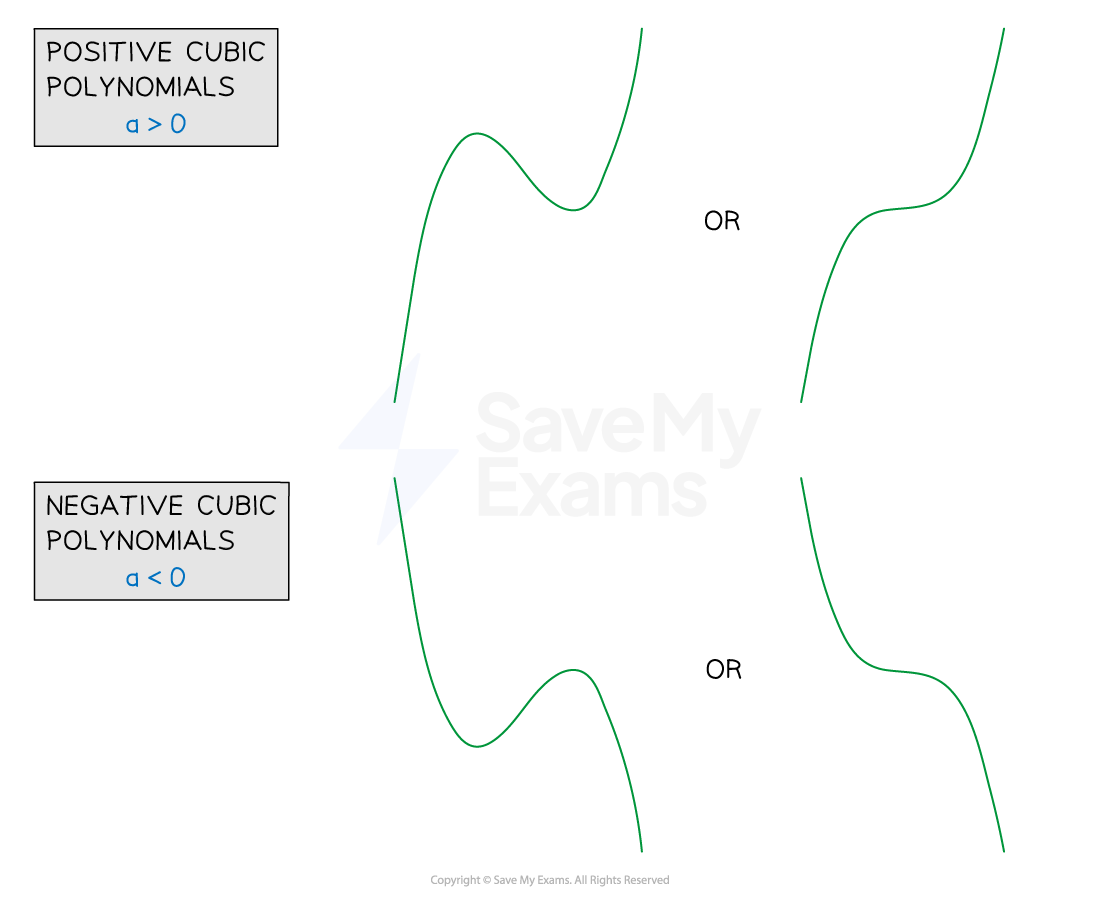
  • In general the graph of a cubic will take one of four forms

    • All are smooth curves

General shape of positive and negative cubic graphs

  • The exact form of a particular cubic will depend on:

    • The number (and value) of roots (x-axis intercepts)

    • The y-axis intercept

    • The sign of the coefficient of the x cubed term (a)

      • If a greater than 0 the graph is a positive cubic ('starts' in the bottom left, 'ends' in the top right)

      • If a less than 0 the graph is a negative cubic ('starts' in the top left, 'ends' in the bottom right)

    • The turning points

Key features of a polynomial graph - shape, intercept, turning points

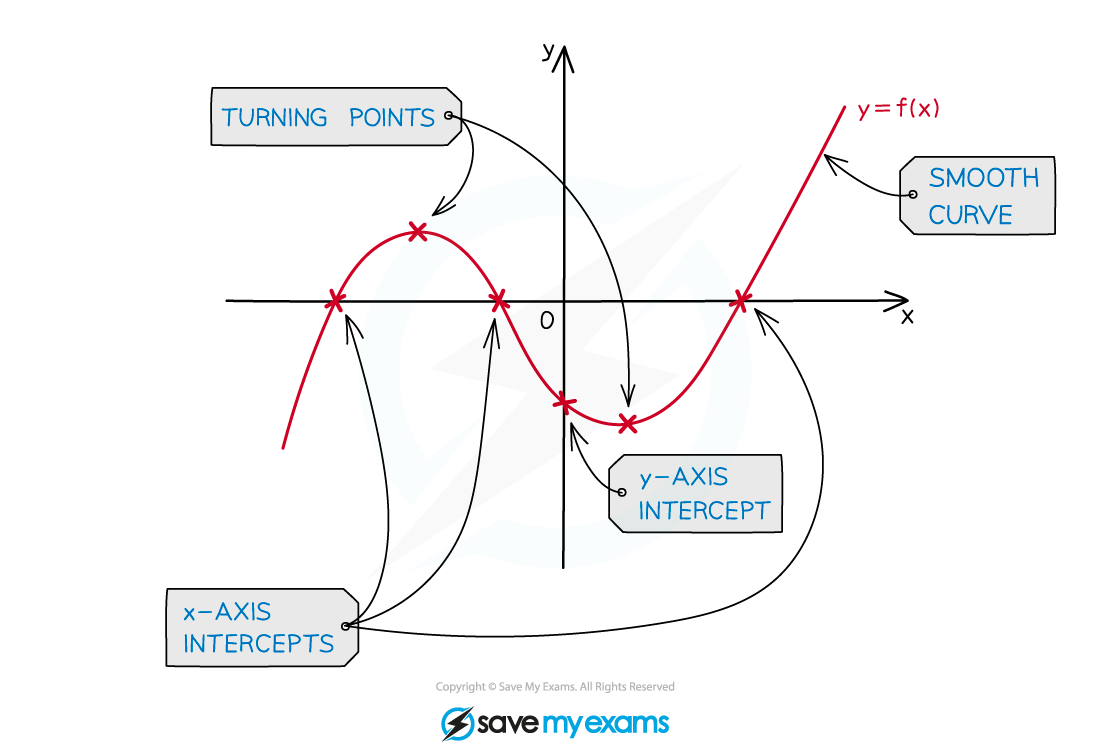
  • Cubics can have two turning points

    • a maximum point and a minimum point

  • However, note that the graphs of y equals x cubed and y equals negative x cubed:

    • Do not have a maximum or minimum (no turning points)

    • Only cross the x-axis once, at x equals 0

How do I sketch the graph of a cubic?

  • STEP 1
    Find the y-axis intercept by setting x equals 0

  • STEP 2
    Find the x-axis intercepts (roots) by setting y equals 0

    • In factorised form, this can be done by inspection

      • A cubic of the form y equals open parentheses x minus p close parentheses open parentheses x minus q close parentheses open parentheses x minus r close parentheses has roots at p comma space q and r

      • E.g. y equals open parentheses x minus 2 close parentheses open parentheses x minus 3 close parentheses open parentheses x plus 5 close parentheses has roots at 2, 3, and -5

    • Any repeated roots will mean the graph touches the x-axis

      • The graph does not cross the x-axis

      • E.g. open parentheses x minus 2 close parentheses squared open parentheses x plus 1 close parentheses touches the x-axis at x equals 2, and intersects the x-axis at x equals negative 1

  • STEP 3
    Consider the shape of the graph

    • Is it a positive cubic or a negative cubic?

    • Where does the graph 'start' and 'end'?

  • STEP 4
    Consider where any turning points should go

  • STEP 5
    Sketch the graph with a smooth curve
    Label points where the graph intercepts the x and y axes

Worked Example

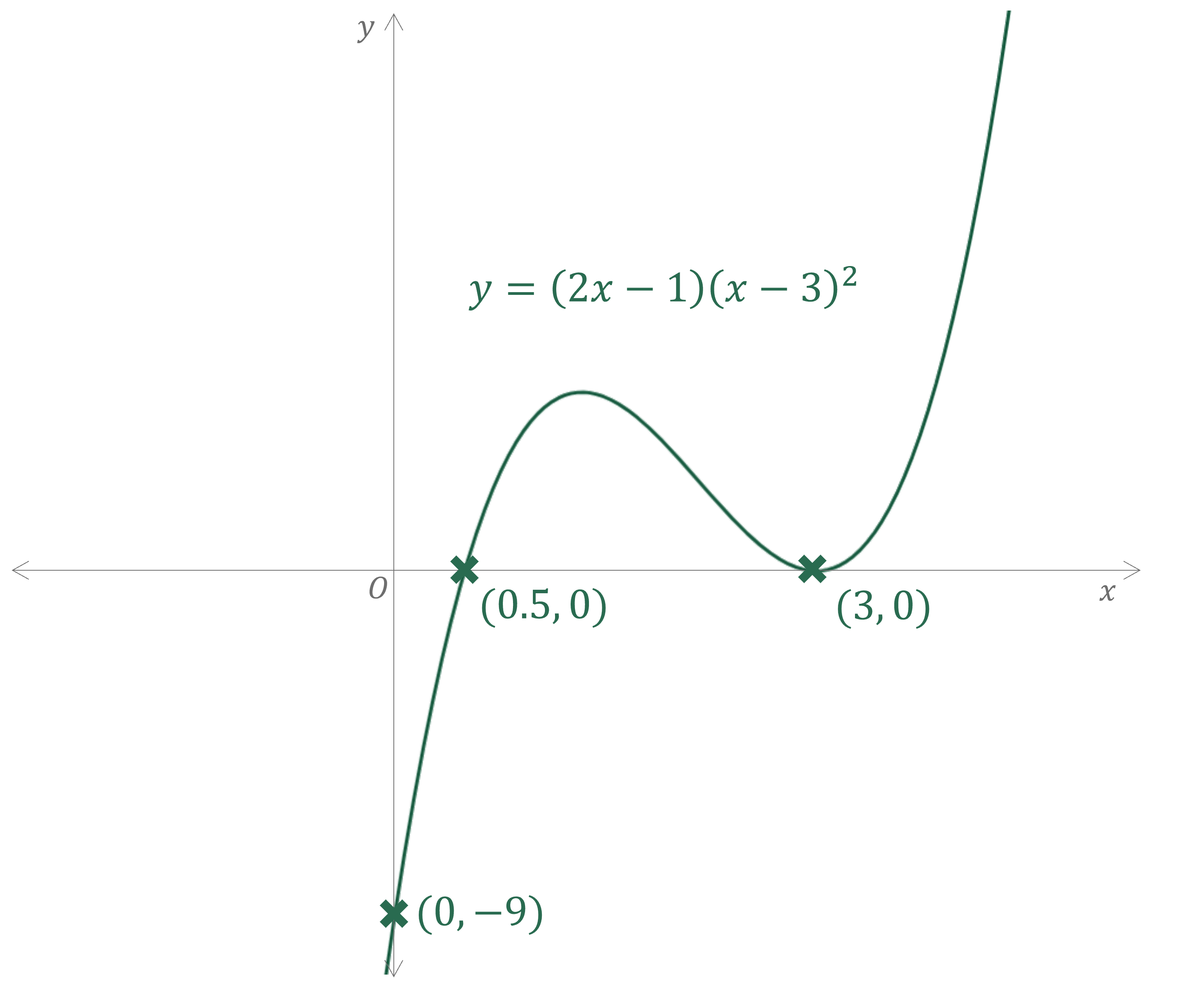
Sketch the graph of y equals open parentheses 2 x minus 1 close parentheses open parentheses x minus 3 close parentheses squared.

Answer:

STEP 1
Find the y-axis intercept by substituting in x equals 0

y equals open parentheses negative 1 close parentheses open parentheses negative 3 close parentheses squared equals negative 9

STEP 2
Find the x-axis intercepts by solving y equals 0
Either bracket can be equal to zero

table row cell open parentheses 2 x minus 1 close parentheses end cell equals cell 0 space end cell row cell space x end cell equals cell 1 half end cell end table

table row cell open parentheses x minus 3 close parentheses squared end cell equals 0 row x equals 3 end table
(repeated solution, as there are two open parentheses x minus 3 close parentheses brackets

STEP 3
Consider the shape, and the 'start' and 'end' points:

a greater than 0 space open parentheses a equals 2 close parentheses so it is a positive cubic
x equals 3 is a repeated root so the graph will touch the x-axis at this point (but not cross it)

STEP 4
Consider the turning points

One turning point (minimum) will need to be where the curve touches the x-axis
The other (maximum) will need to be between the two roots x equals 1 half and x equals 3

STEP 5
Sketch a smooth curve with labelled intercepts

Worked example - final answer sketch of cubic showing intersections

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Quadratic GraphsNext:Reciprocal Graphs
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Jamie Wood

    Reviewer: Jamie Wood

    Expertise: Maths Content Creator

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.