Reciprocal Graphs (Edexcel IGCSE Maths B): Revision Note
Exam code: 4MB1
Reciprocal Graphs
What is a reciprocal graph?
A reciprocal graph is of the form
or
These graphs do not have any y-intercepts
and do not have any roots
This means that the curves do not cross either the x- or y-axes
The two basic reciprocal graphs have
I.e.
or

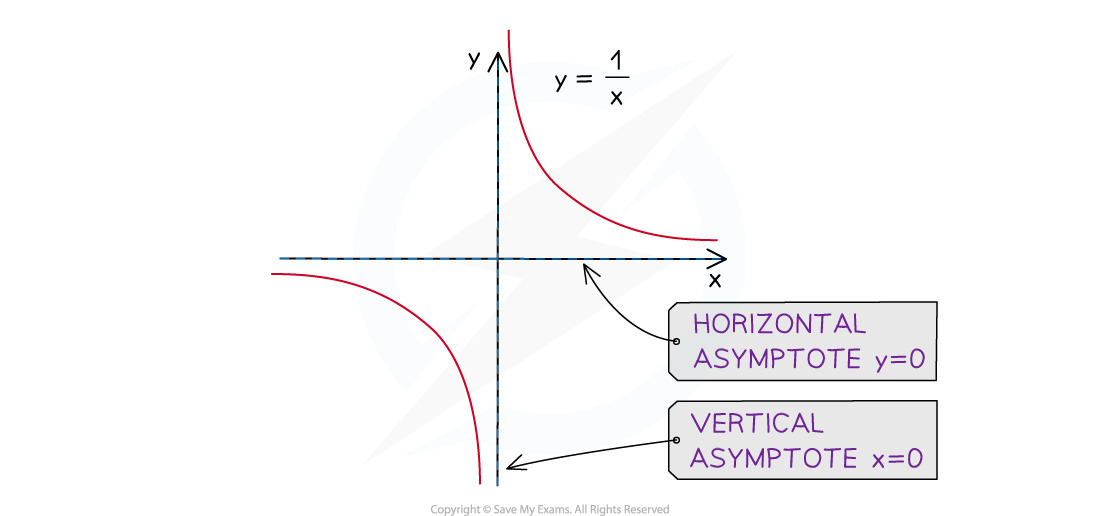
What are the asymptotes on a reciprocal graph?
An asymptote is a line on a graph that a curve becomes closer and closer to but never touches
These may be horizontal or vertical lines
A reciprocal graph has two asymptotes
A horizontal asymptote along the x-axis (with equation
)
This is the limiting value of y when the value of x gets very large (either positive or negative)
A vertical asymptote along the y-axis (with equation
)
This shows the problem of trying to divide by zero
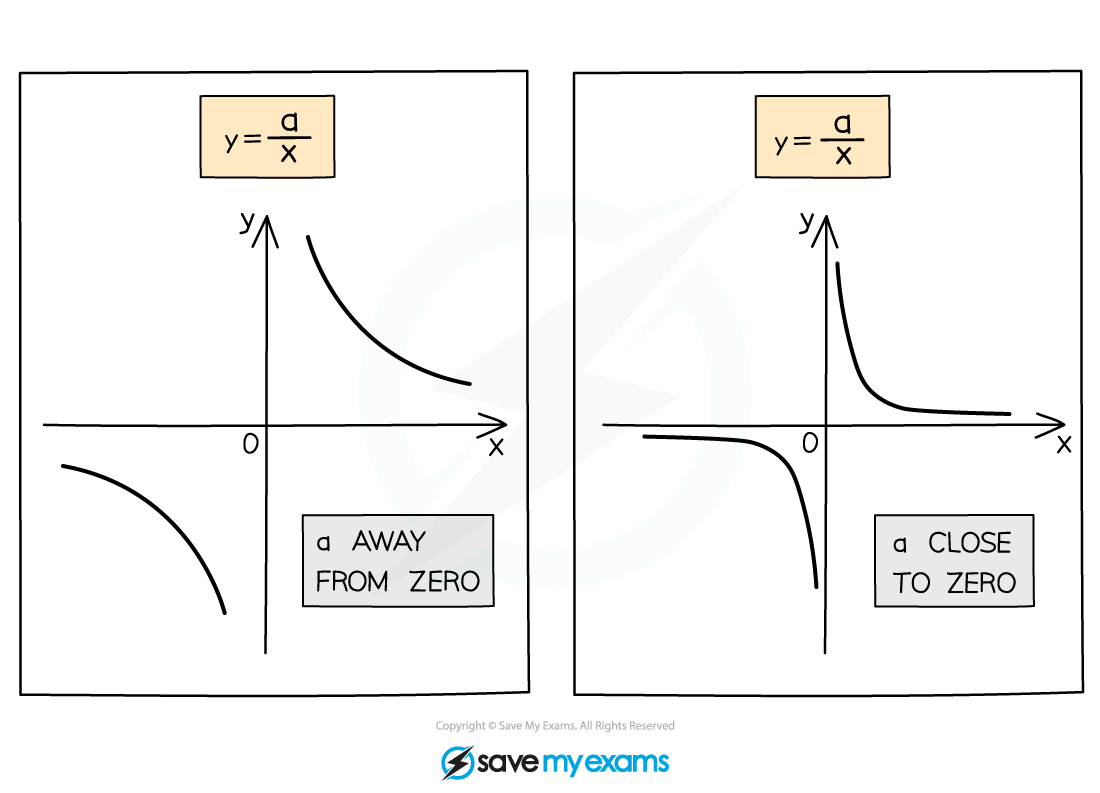
What if a is not equal to 1?
You also need to recognise graphs of
and
when
In the graphs below the asymptotes are shown by dashed lines

The sign of a shows where the curves are located
The size of a shows how steep the curves are
The closer a is to 0 the more L-shaped the curves are
What if a constant is added to the equation?
The reciprocal graphs,
and
(where
and
are both constants)
are the same shapes as
or
but are shifted upwards by
units
would be
shifted up by 2 units
would be
shifted down by 3 units
This means the horizontal asymptote also shifts up by
units,
The equation of the horizontal asymptote is
would have a horizontal asymptote at
would have a horizontal asymptote at
The vertical asymptote remains along the y-axis
The equation of the vertical asymptote is
and
would both have vertical asymptotes at
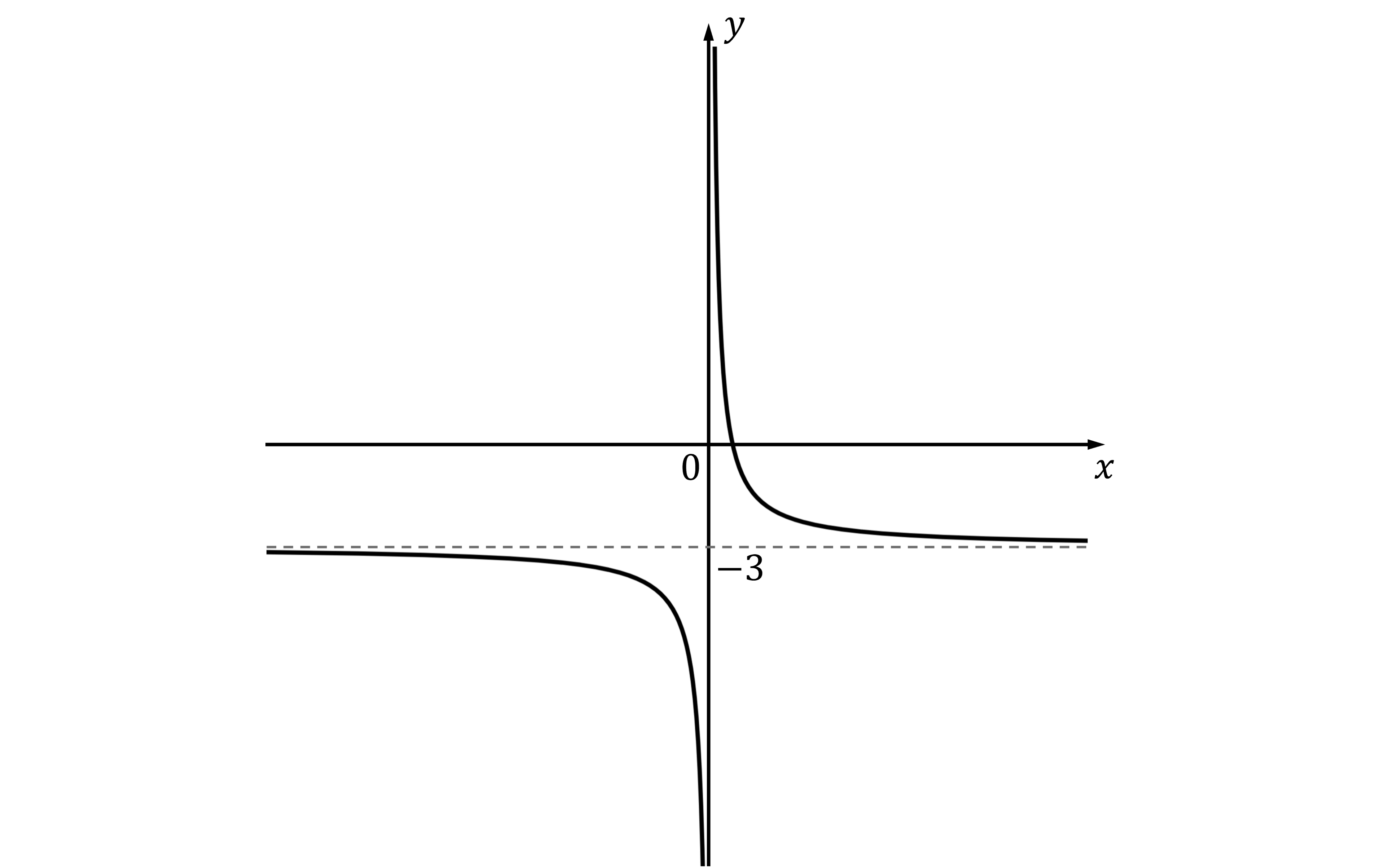
Worked Example
Sketch the graph of .
Answer:
The graph of
will have the same basic shape as
(For a sketch, you don't need to worry abut the effect of the '2')
but shifted down by 3 units because of the -3
(This means it will have an asymptote at
)
It can be useful to sketch the asymptote first, to give you a 'guideline' for the rest of the sketch

Unlock more, it's free!
Was this revision note helpful?
