IGCSEMathsEdexcelMaths BRevision NotesMatricesTransformations using MatricesDeterminant of a Transformation Matrix

Determinant of a Transformation Matrix (Edexcel IGCSE Maths B): Revision Note

Exam code: 4MB1

Roger B

Written by: Roger B

Reviewed by: Jamie Wood

Updated on

Determinant of a transformation matrix

What does the determinant of a transformation matrix represent?

  • When a 2×2 matrix is used to represent a transformation

    • the determinant of the matrix is the area scale factor of the transformation

    • I.e. the area of a transformed shape is equal to

      • the area of the original shape

      • times the determinant of the transformation matrix

  • The determinant of a 2×2 matrix open parentheses table row a b row c d end table close parentheses is a d minus b c

Worked Example

A triangle has vertices with coordinates (1, -3), (7, -3) and (3, 1).

(a) Find the coordinates of the vertices of the image triangle when that triangle is transformed by the matrix M equals open parentheses table row cell negative square root of 3 end cell cell negative 1 end cell row 1 cell negative square root of 3 end cell end table close parentheses.

Answer:

You can represent the triangle as a 2×3 matrix of vertices

  • This will be the coordinates of the vertices as column vectors, but written in a single matrix

open parentheses table row 1 7 3 row cell negative 3 end cell cell negative 3 end cell 1 end table close parentheses

To transform the triangle, multiply its matrix by the transformation matrix bold M

table row blank blank cell open parentheses table row cell negative square root of 3 end cell cell negative 1 end cell row 1 cell negative square root of 3 end cell end table close parentheses open parentheses table row 1 7 3 row cell negative 3 end cell cell negative 3 end cell 1 end table close parentheses end cell row blank equals cell open parentheses table row cell open parentheses negative square root of 3 close parentheses cross times 1 plus open parentheses negative 1 close parentheses cross times open parentheses negative 3 close parentheses end cell cell open parentheses negative square root of 3 close parentheses cross times 7 plus open parentheses negative 1 close parentheses cross times open parentheses negative 3 close parentheses end cell cell open parentheses negative square root of 3 close parentheses cross times 3 plus open parentheses negative 1 close parentheses cross times 1 end cell row cell 1 cross times 1 plus open parentheses negative square root of 3 close parentheses cross times open parentheses negative 3 close parentheses end cell cell 1 cross times 7 plus open parentheses negative square root of 3 close parentheses cross times open parentheses negative 3 close parentheses end cell cell 1 cross times 3 plus open parentheses negative square root of 3 close parentheses cross times 1 end cell end table close parentheses end cell row blank equals cell open parentheses table row cell 3 minus square root of 3 space end cell cell space 3 minus 7 square root of 3 space end cell cell space minus 1 minus 3 square root of 3 end cell row cell 1 plus 3 square root of 3 space end cell cell space 7 plus 3 square root of 3 space end cell cell space 3 minus square root of 3 end cell end table close parentheses end cell end table

Write the new vertices as coordinates

open parentheses 3 minus square root of 3 comma space 1 plus 3 square root of 3 close parentheses, open parentheses 3 minus 7 square root of 3 comma space 7 plus 3 square root of 3 close parentheses and open parentheses negative 1 minus 3 square root of 3 comma space 3 minus square root of 3 close parentheses
 

(b) Find the area of the image triangle.

Answer:

The original and transformed triangles look like this:

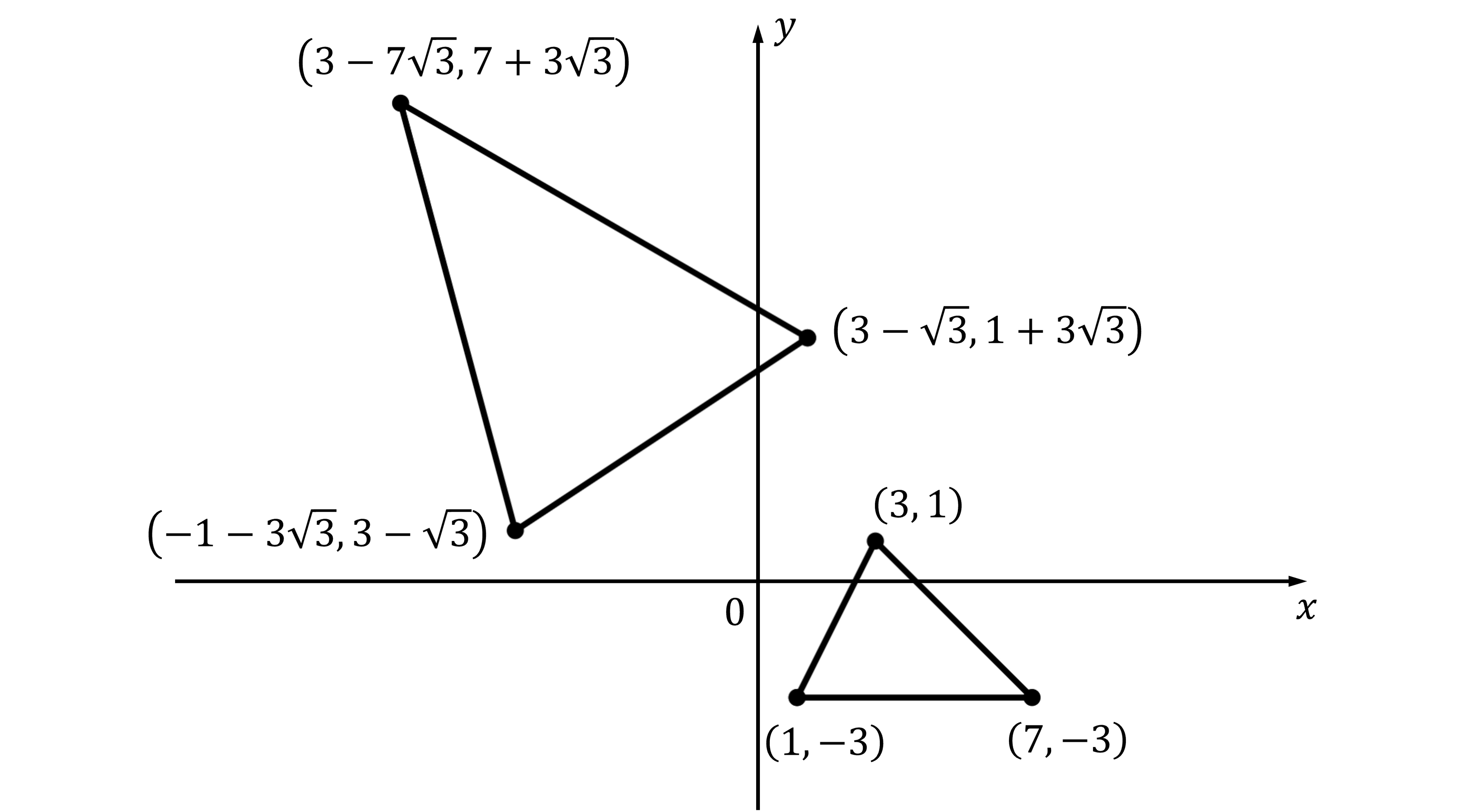
A graph showing two triangles. The larger triangle has vertices with surds, and the smaller triangle below has vertices at (1,-3), (3,1), and (7,-3).

Trying to calculate the area of the transformed triangle directly would be quite challenging, to say the least!

However the area of the original triangle is easy to calculate

  • It has a base of 6, and a height of 4

  • Use Area equals 1 half cross times base cross times height

area space of space original space triangle equals 1 half cross times 6 cross times 4 equals 12

Find the determinant of the transformation matrix M equals open parentheses table row cell negative square root of 3 end cell cell negative 1 end cell row 1 cell negative square root of 3 end cell end table close parentheses

  • The determinant of a 2×2 matrix open parentheses table row a b row c d end table close parentheses is a d minus b c

table row cell determinant space of space M end cell equals cell open parentheses negative square root of 3 close parentheses cross times open parentheses negative square root of 3 close parentheses minus open parentheses negative 1 close parentheses cross times 1 end cell row blank equals cell 3 minus open parentheses negative 1 close parentheses end cell row blank equals 4 end table

That is the area scale factor of the transformation

  • So multiply the original area by 4 to find the transformed area

12 cross times 4 equals 48

Area of the image triangle is 48

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Enlargement MatricesNext:Combining Matrix Transformations
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Jamie Wood

    Reviewer: Jamie Wood

    Expertise: Maths Content Creator

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.