IGCSEMathsEdexcelMaths BRevision NotesVectors & Transformation GeometryVectorsParallel Vectors & Unit Vectors

Parallel Vectors & Unit Vectors (Edexcel IGCSE Maths B): Revision Note

Exam code: 4MB1

Roger B

Written by: Roger B

Reviewed by: Jamie Wood

Updated on

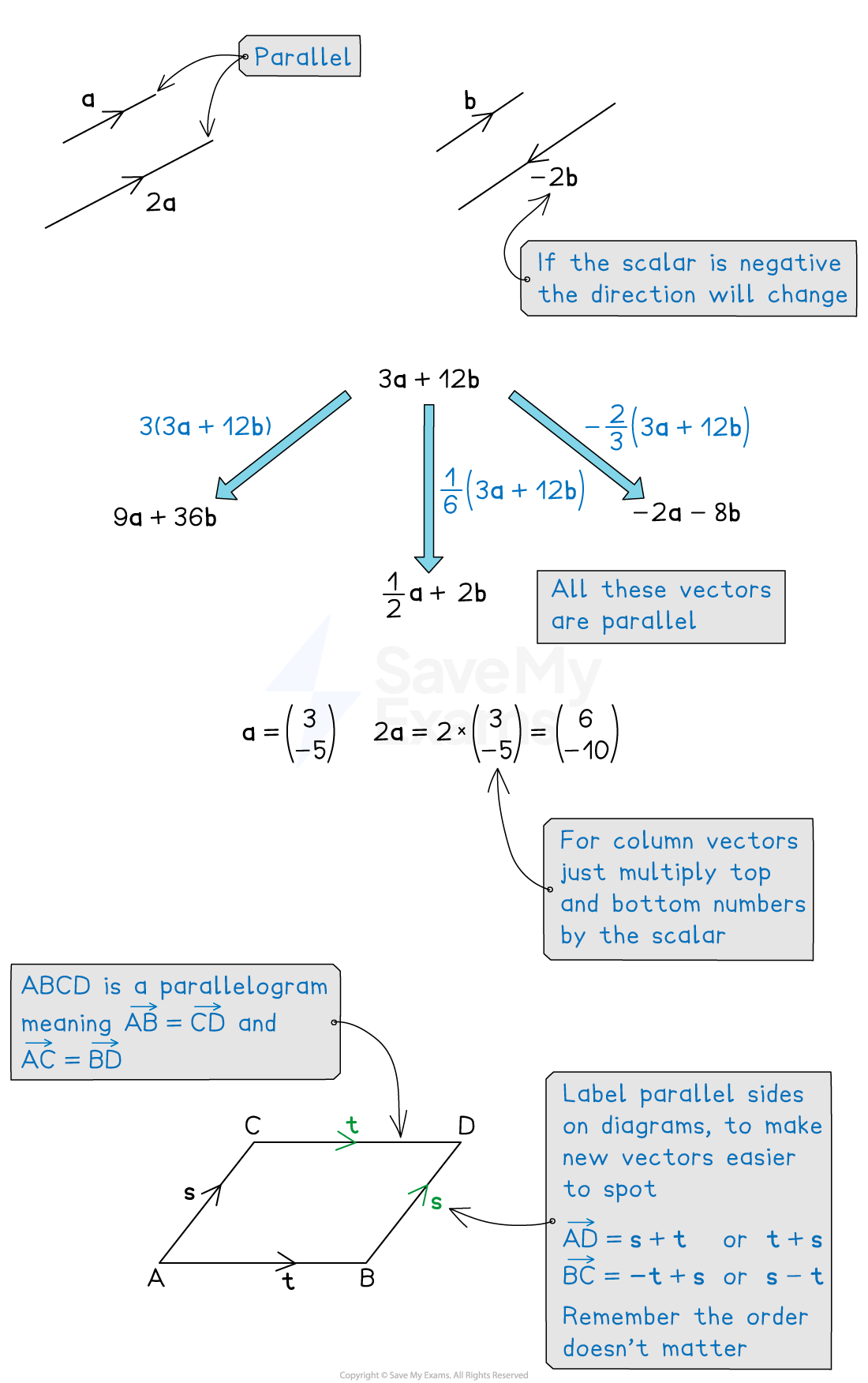
Parallel vectors

How can I tell if two vectors are parallel?

  • Two vectors are parallel if one is a scalar multiple of the other

    • This means that all components of the vector have been multiplied by a common constant (scalar)

    • For example, open parentheses table row 1 row 3 end table close parentheses and open parentheses table row 2 row 6 end table close parentheses are scalar multiples

      • The numbers in the first vector have each been multiplied by 2 to get the numbers in the second vector

  • Multiplying the components of a vector by a positive scalar changes the magnitude of the vector but not the direction

    • For example, open parentheses table row 2 row 6 end table close parentheses is double the length of open parentheses table row 1 row 3 end table close parentheses but in the same direction

  • Multiplying the components of a vector by a negative scalar reverses the direction

  • You can factorise a vector to help spot if two vectors are parallel

    • open parentheses table row 9 row cell negative 3 end cell end table close parentheses equals 3 open parentheses table row 3 row cell negative 1 end cell end table close parentheses

    • open parentheses table row cell negative 6 end cell row 2 end table close parentheses equals negative 2 open parentheses table row 3 row cell negative 1 end cell end table close parentheses

      • They are scalar multiples of the same vector so they are parallel

Diagram illustrating parallel vectors with examples using scalars. Includes vector equations, rules for column and i/j vectors, and a parallelogram ABCD.
Examples of parallel vectors

Examiner Tips and Tricks

If you are told that two vectors (bold a and bold b) are parallel, then it can be helpful to define a scalar to form an equation bold a equals k bold b .

Worked Example

Show that the vectors bold a equals open parentheses table row 2 row cell negative 4 end cell end table close parentheses and bold b equals open parentheses table row cell negative 3 end cell row 6 end table close parentheses are parallel.

Answer:

Method 1

Show that one vector is a multiple of the other

table row cell negative 1.5 bold a end cell equals cell negative 1.5 open parentheses table row 2 row cell negative 4 end cell end table close parentheses end cell row blank equals cell open parentheses table row cell negative 1.5 cross times 2 end cell row cell negative 1.5 cross times negative 4 end cell end table close parentheses end cell row blank equals cell open parentheses table row cell negative 3 end cell row 6 end table close parentheses end cell row blank equals bold b end table

bold b equals negative 1.5 bold a, so the two vectors are parallel

Method 2

Show that both vectors are multiples of another vector

bold a equals open parentheses table row 2 row cell negative 4 end cell end table close parentheses equals 2 open parentheses table row 1 row cell negative 2 end cell end table close parentheses

bold b equals open parentheses table row cell negative 3 end cell row 6 end table close parentheses equals negative 3 open parentheses table row 1 row cell negative 2 end cell end table close parentheses

bold a and bold b are both scalar multiples of open parentheses table row 1 row cell negative 2 end cell end table close parentheses, so they are parallel to each other

Unit vectors

What is a unit vector?

  • A unit vector is a vector with a modulus (length) of 1

  • To find a unit vector that is in the same direction as the vector bold a

    • divide the components of the vector by the modulus of the vector

    • I.e. fraction numerator bold a over denominator open vertical bar bold a close vertical bar end fraction is a unit vector in the direction of vector bold a

  • For example, a unit vector in the direction open parentheses table row 3 row cell negative 4 end cell end table close parentheses is

table row cell fraction numerator 1 over denominator square root of 3 squared plus open parentheses negative 4 close parentheses squared end root end fraction open parentheses table row 3 row cell negative 4 end cell end table close parentheses end cell equals cell 1 fifth open parentheses table row 3 row cell negative 4 end cell end table close parentheses end cell row blank equals cell open parentheses table row cell 3 over 5 end cell row cell negative 4 over 5 end cell end table close parentheses end cell end table

Worked Example

Find a unit vector in the same direction as open parentheses table row cell negative 2 end cell row 5 end table close parentheses.

Answer:

Find the modulus of the vector

square root of open parentheses negative 2 close parentheses squared plus 5 squared end root equals square root of 4 plus 25 end root equals square root of 29

Divide each of the vector components by the modulus

open parentheses table row cell negative fraction numerator 2 over denominator square root of 29 end fraction end cell row cell fraction numerator 5 over denominator square root of 29 end fraction end cell end table close parentheses

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Position & Displacement VectorsNext:Finding Vector Paths
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Jamie Wood

    Reviewer: Jamie Wood

    Expertise: Maths Content Creator

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.