Solving Equations Using Trigonometric Graphs (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Using trigonometric graphs
How do I solve trig equations?
The inverse trig functions on your GDC will only give you one solution to a trig equation
This solution is called the principal value
e.g.
is the principal value for the equation
You can use the trig graphs and their symmetries to find the other solutions within an interval
How do I determine the number of solutions?
For
and
where
and
There are always two solutions in any interval of length 360°
Divide the width of the interval by 360°
If it is a whole number then double it to get the number of solutions
Otherwise, double the closest whole numbers to find the minimum and maximum number of solutions
Examiner Tips and Tricks
Be careful when , there is at least one solution every 360°. There could be 2 solutions depending on where the interval starts.
Be careful when , there are at least two solutions every 360°. There could be 3 solutions depending on where the interval starts.
For
There is always one solution in any interval of length 180°
Divide the width of the interval by 180°
If it is a whole number then this is equal to the number of solutions
Otherwise, the closest whole numbers are the minimum and maximum number of solutions
How do I use trig graphs to solve trig equations?
STEP 1
Sketch the graph for the given function and intervalCheck whether you should be working in degrees or radians
Label the axes with the key values (0°, 90°, 180°, etc)
STEP 2
Draw a horizontal line going through the y-axis at the relevant pointe.g. to solve
draw the line
STEP 3
Find the principal value and mark it on the graphSTEP 4
Use the symmetry and periodicity of the graph to find all the solutions in the intervalis symmetrical about
and repeats every 360°
If
a solution, then
is also a solution
is symmetrical about
and repeats every 360°
If
a solution, then
is also a solution
repeats every 180°
If
a solution, then
is also a solution
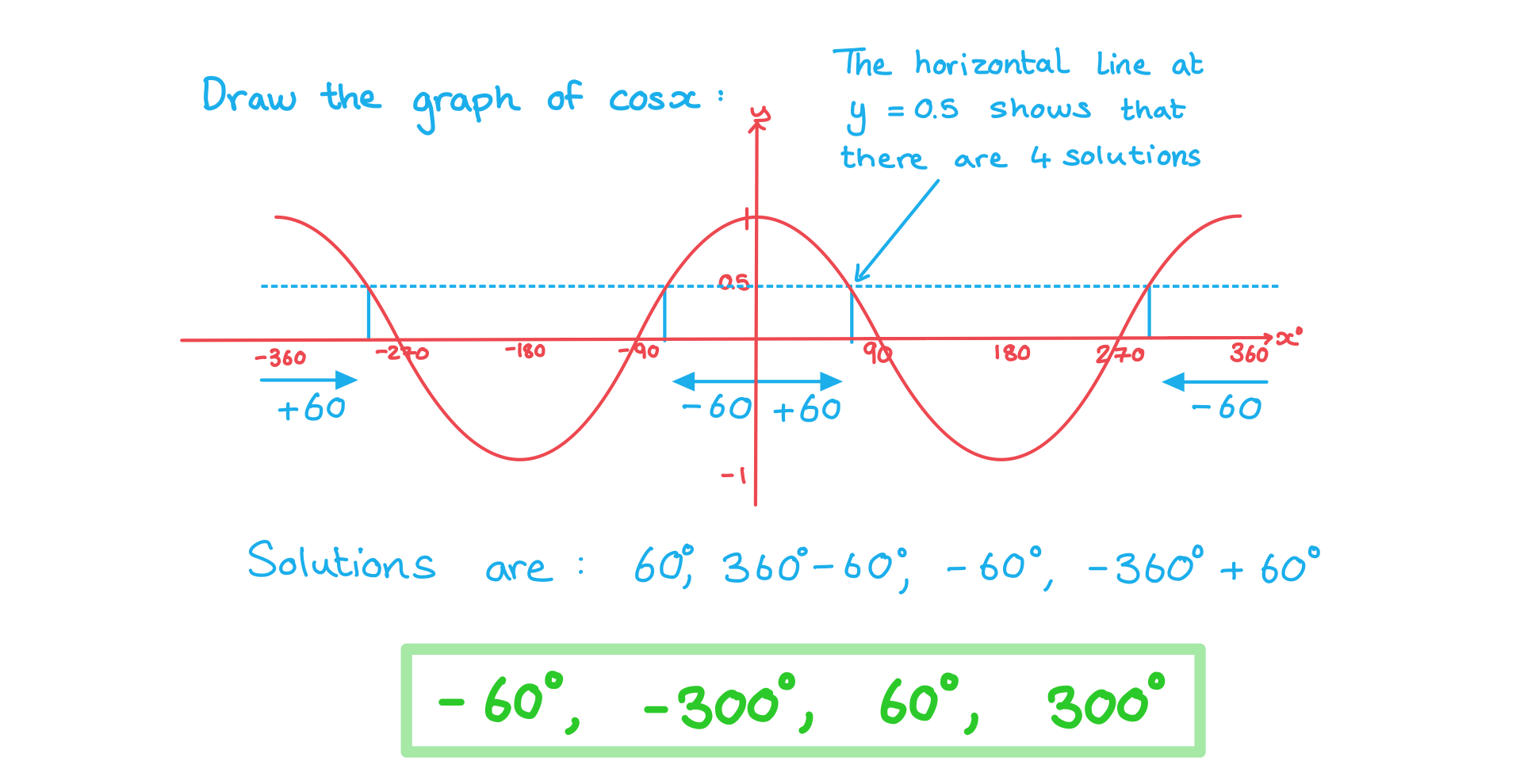
Worked Example
One solution to cos x = 0.5 is 60°. Find all the other solutions in the range -360° ≤ x ≤ 360°.
Answer:

Unlock more, it's free!
Was this revision note helpful?