Processing Uncertainties in Chemistry (DP IB Chemistry): Revision Note

Processing uncertainties in chemistry

What is uncertainty?

• Uncertainty is quantitative indication of the quality of the result 

  • It is the difference between the actual reading taken (caused by the equipment or techniques used) and the true value

  • It is a range of values around a measurement within which the true value is expected to lie and is an estimate

• Uncertainties are not the same as errors

  • Errors arise from equipment or practical techniques that cause a reading to be different from the true value

• Uncertainties in measurements are recorded as a range (±) to an appropriate level of precision

Table showing different uncertainties

Types of uncertainty

• Uncertainty is grouped into three main types:

  • Absolute uncertainty

    • The actual amount by which the quantity is uncertain

    • e.g.if v = 5.0 ± 0.1 cm, the absolute uncertainty in v is 0.1 cm

  • Fractional uncertainty

    • The absolute uncertainty divided by the quantity itself

    • e.g.if v = 5.0 ± 0.1 cm, the fractional uncertainty in v is =

  • Percentage uncertainty

    • The ratio of the expanded uncertainty to the measured quantity on a scale relative to 100%

    • This is calculated using the following formula:

Percentage uncertainty = 

How to calculate absolute, fractional and percentage uncertainty

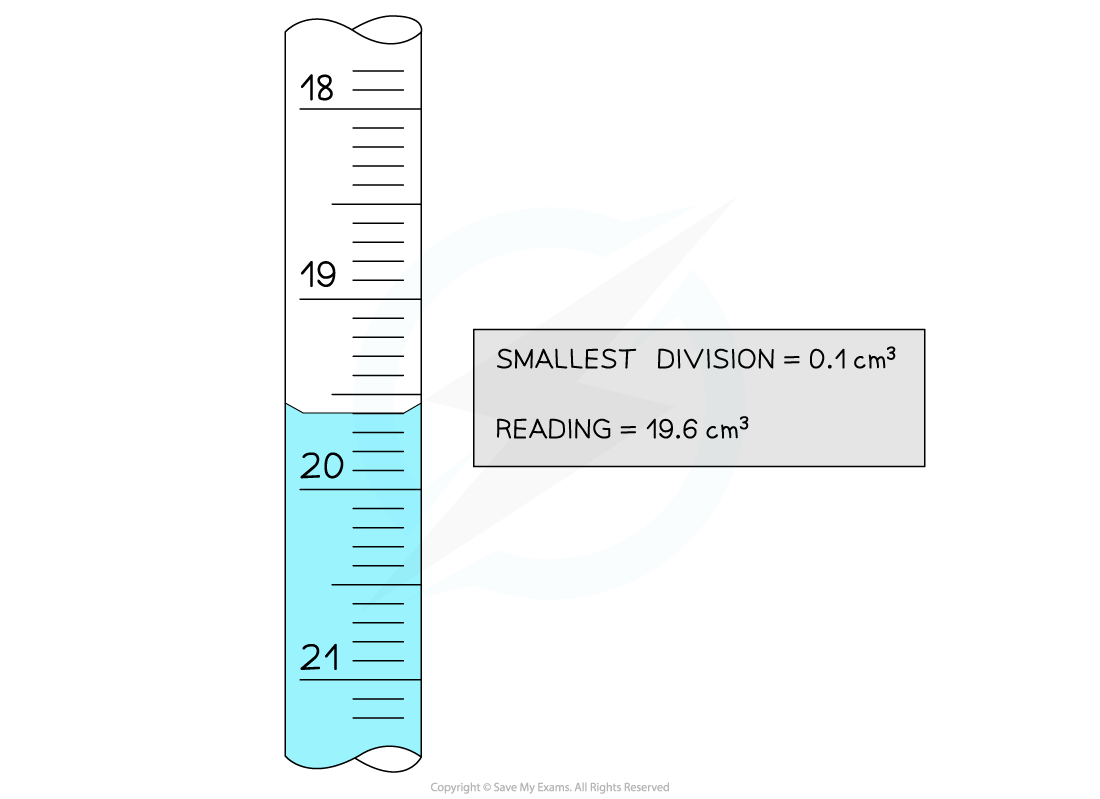
• The uncertainties in this reading are:

  • Absolute

    • Uncertainty = = 0.05 cm³ 

    • Reading = 19.6 ± 0.05 cm³ 

  • Fractional

    • Uncertainty =  =  =  cm³ 

  • Percentage

    • Uncertainty =  =  = 0.5%

    • Reading = 19.6 ± 0.5% cm³ 

Propagating uncertainties in processed data

• Uncertainty propagates in different ways depending on the type of calculation involved

Adding or subtracting measurements

• When you are adding or subtracting two measurements then you add together the absolute measurement uncertainties

• For example:

  • Using a balance to measure the initial and final mass of a container

  • Using a thermometer to measure the temperature at the start and end

  • Using a burette to measure the initial and final readings

• In all of these cases, the instrument is read twice to obtain the final value (e.g. change in mass, temperature, or volume)

  • If the measurement is uncertain by a fixed amount each time, then the total uncertainty is potentially doubled

  • For example:

    • If each reading has an uncertainty of ±0.1 g, the total uncertainty becomes ±0.2 g

Multiplying or dividing measurements

• When you multiply or divide experimental measurements then you add together the percentage uncertainties

• You can then calculate the absolute uncertainty from the sum of the percentage uncertainties

Exponential measurements (HL only)

• When experimental measurements are raised to a power, you multiply the fractional or percentage uncertainty by the power

The coefficient of determination, R²

• The coefficient of determination is a measure of fit that can be applied to lines and curves on graphs

• The coefficient of determination is written as R² 

• It is used to evaluate the fit of a trend line / curve:

  • R² = 0

    • The dependent variable cannot be predicted from the independent variable. 

    • R² is usually greater than or equal to zero

  • R² between 0 and 1

    • The dependent variable can be predicted from the independent variable, although the degree of success depends on the value of R² 

    • The closer to 1, the better the fit of the trend line / curve

  • R² = 1

    • The dependent variable can be predicted from the independent variable

    • The trend line / curve is perfect 

    • Note: This does not guarantee that the trend line / curve is a good model for the relationship between the dependent and independent variables