Stretches of Graphs (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Stretches of graphs
What are stretches of graphs?
A stretch is when
the graph is stretched vertically or horizontally
by a scale factor,
The size of the graph changes
The orientation of the graph remains unchanged
Stretches act parallel to a coordinate axis
e.g. for a vertical stretch of scale factor
points above the
-axis move vertically upwards
points below the
-axis move vertically downwards
i.e. a vertical stretch acts parallel to the
-axis

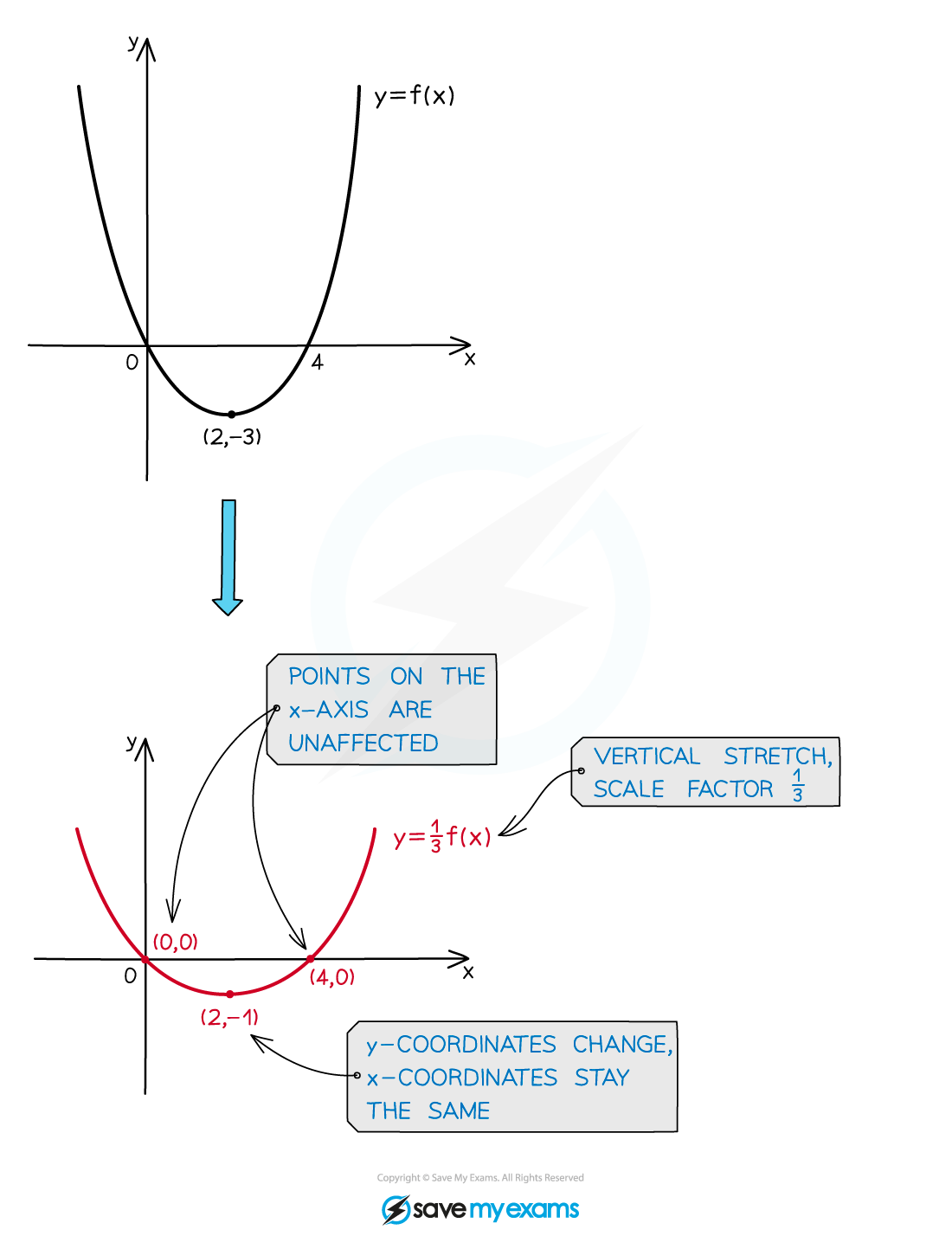
How do I find the graph equation after a vertical stretch?
A vertical stretch of the graph
by a scale factor
parallel to the
-axis has the equation
Any horizontal asymptotes change
becomes
Vertical asymptotes stay the same
If the scale factor is
, then points
above the
-axis stretch upwards
below the
-axis stretch downwards
, then points
above the
-axis "compress / squash" downwards
below the
-axis "compress / squash" upwards
Examiner Tips and Tricks
Do not use the words squash or compress in the exam - instead use sentences like "a stretch by a scale factor of ".
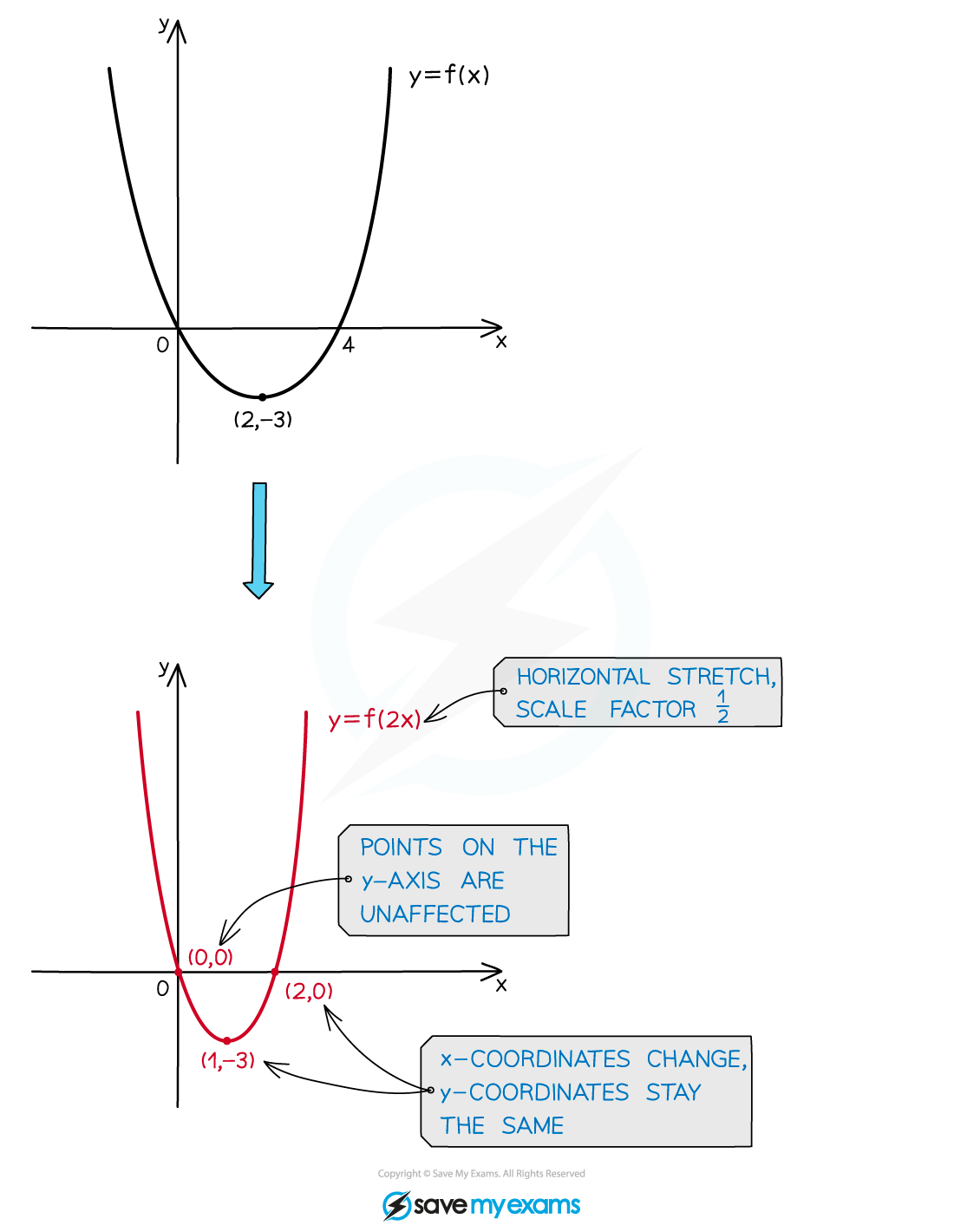
How do I find the graph equation after a horizontal stretch?
A horizontal stretch of the graph
by a scale factor
parallel to the
-axis has the equation
Any horizontal asymptotes stay the same
but vertical asymptotes change
e.g.
becomes
Examiner Tips and Tricks
It is a common mistake to think a horizontal stretch of scale factor has the equation
.
This means the equation
where
represents
a horizontal stretch of scale factor
i.e. a horizontal "compression / squash" of scale factor
Worked Example
The diagram below shows the graph of .
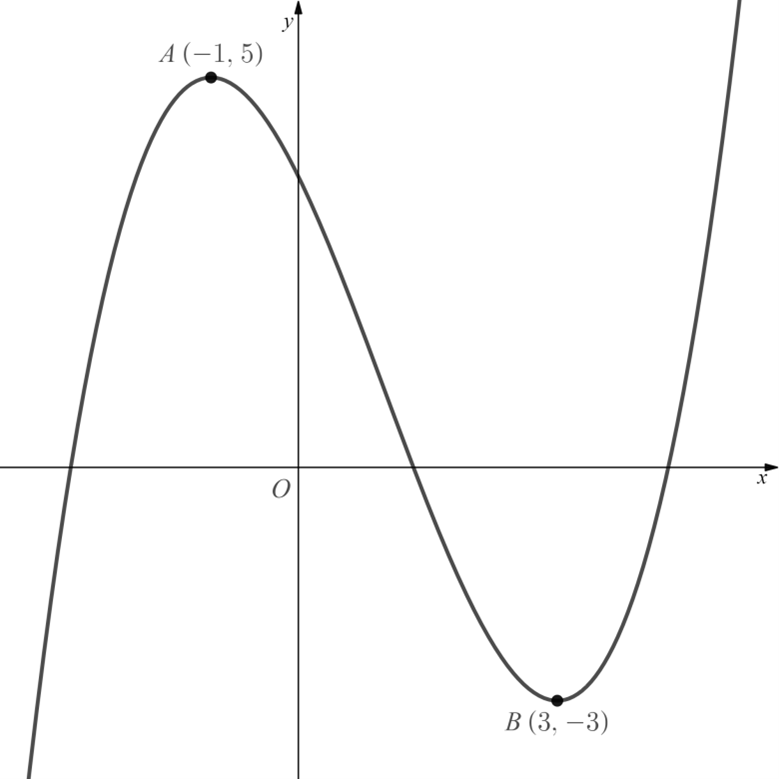
(a) Sketch the graph of .
Answer:

(b) Sketch the graph of .
Answer:


Unlock more, it's free!
Did this page help you?