Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)SLRevision Notes3. Geometry & TrigonometryGeometry ToolkitArcs & Sectors Using Degrees

Arcs & Sectors Using Degrees (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

DP Analysis & Approaches (AA): SLDP Analysis & Approaches (AA): HLDP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SL
Formulae for sector area and arc length on left; diagram of a sector with angle θ and radius r on right.
Arcs and sectors of circles

Did this video help you?

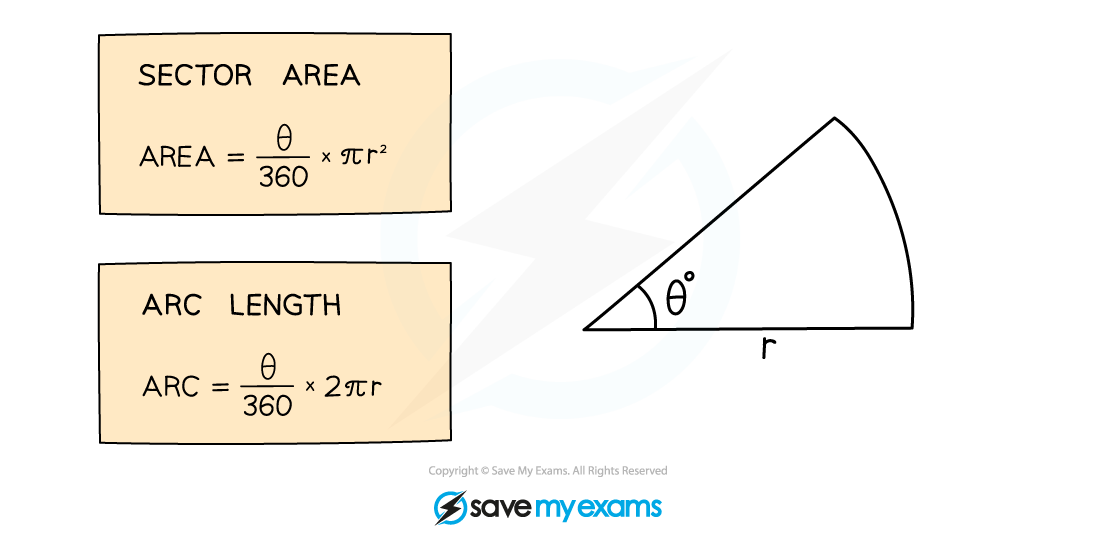
Length of an Arc

What is an arc?

  • An arc is a part of the circumference of a circle

    • It is easiest to think of it as the crust of a single slice of pizza

  • If the angle at the centre is less than 180° then the arc is known as a minor arc

  • If the angle at the centre is more than 180° then the arc is known as a major arc

How do I find the length of an arc?

  • The length of an arc is simply a fraction of the circumference of a circle

    • The fraction can be found by dividing the angle at the centre by 360°

  • The formula is l equals theta over 360 cross times 2 straight pi r

    • l is the length of the arc

    • theta is the angle measured in degrees

    • r is the radius

Examiner Tips and Tricks

This is not given in the formula booklet. However, you are the formula for when the angle is measured in radians.

Examiner Tips and Tricks

Make sure that you read the question carefully to determine if you need to calculate the arc length of a sector, the perimeter or something else that incorporates the arc length!

Worked Example

A circular pizza has had a slice cut from it, the angle of the slice that was cut was 38 °. The radius of the pizza is 12 cm. Find 

i) the length of the outside crust of the slice of pizza (the minor arc),

ai-sl-3-1-2-length-arc-we-i

 

ii) the perimeter of the remaining pizza.

ai-sl-3-1-2-length-arcwe-ii

Did this video help you?

Area of a Sector

What is a sector?

  • A sector is a part of a circle enclosed by two radii (radiuses) and an arc

    • It is easier to think of this as the shape of a single slice of pizza

  • If the angle at the centre is less than 180° then the sector is known as a minor sector

  • If the angle at the centre is more than 180° then the sector is known as a major sector

How do I find the area of a sector?

  • The area of a sector is simply a fraction of the area of the whole circle

    • The fraction can be found by dividing the angle at the centre by 360°

  • The formula is A equals theta over 360 cross times straight pi r squared

    • A is the area of the sector

    • theta is the angle measured in degrees

    • r is the radius

Examiner Tips and Tricks

This is not given in the formula booklet. However, you are the formula for when the angle is measured in radians.

Worked Example

Jamie has divided a circle of radius 50 cm into two sectors; a minor sector of angle 100° and a major sector of angle 260°. He is going to paint the minor sector blue and the major sector yellow. Find

i) the area Jamie will paint blue,

ai-sl-3-1-2-area-sectorwe-i

ii) the area Jamie will paint yellow.

ai-sl-3-1-2-area-sectorweii

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Coordinate GeometryNext:Radian Measure
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.