Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes5. CalculusCoupled & Second Order Differential EquationsEquilibrium Points

Equilibrium Points (DP IB Applications & Interpretation (AI)): Revision Note

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

DP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): HL

Equilibrium points

What is an equilibrium point?

  • An equilibrium point for a system of coupled differential equations is a point left parenthesis x comma space y right parenthesis at which both fraction numerator d x over denominator d t end fraction equals 0 and fraction numerator d y over denominator d t end fraction equals 0

  • If a solution trajectory starts on an equilibrium point

    • it will never move from that point

  • For example, consider fraction numerator d x over denominator d t end fraction equals 2 x plus 3 y minus 8 and fraction numerator d y over denominator d t end fraction equals 3 x minus y minus 1

    • Solve 2 x plus 3 y minus 8 equals 0 and 3 x minus y minus 1 equals 0

    • open parentheses 1 comma space 2 close parentheses is the equilibrium point

What are stable and unstable equilibrium points?

  • An equilibrium point can be stable or unstable

  • An equilibrium point is stable if

    • all solution trajectories which start close to the equilibrium point remain close to the equilibrium point

  • An equilibrium point is unstable if

    • there is any solution trajectory which starts close to the equilibrium point and moves away from the equilibrium point

  • A saddle point is an example of an unstable equilibrium point

    • Some solution trajectories which start close to the saddle point move towards the saddle point

    • Whereas other solution trajectories which start close to the saddle point move away from the saddle point

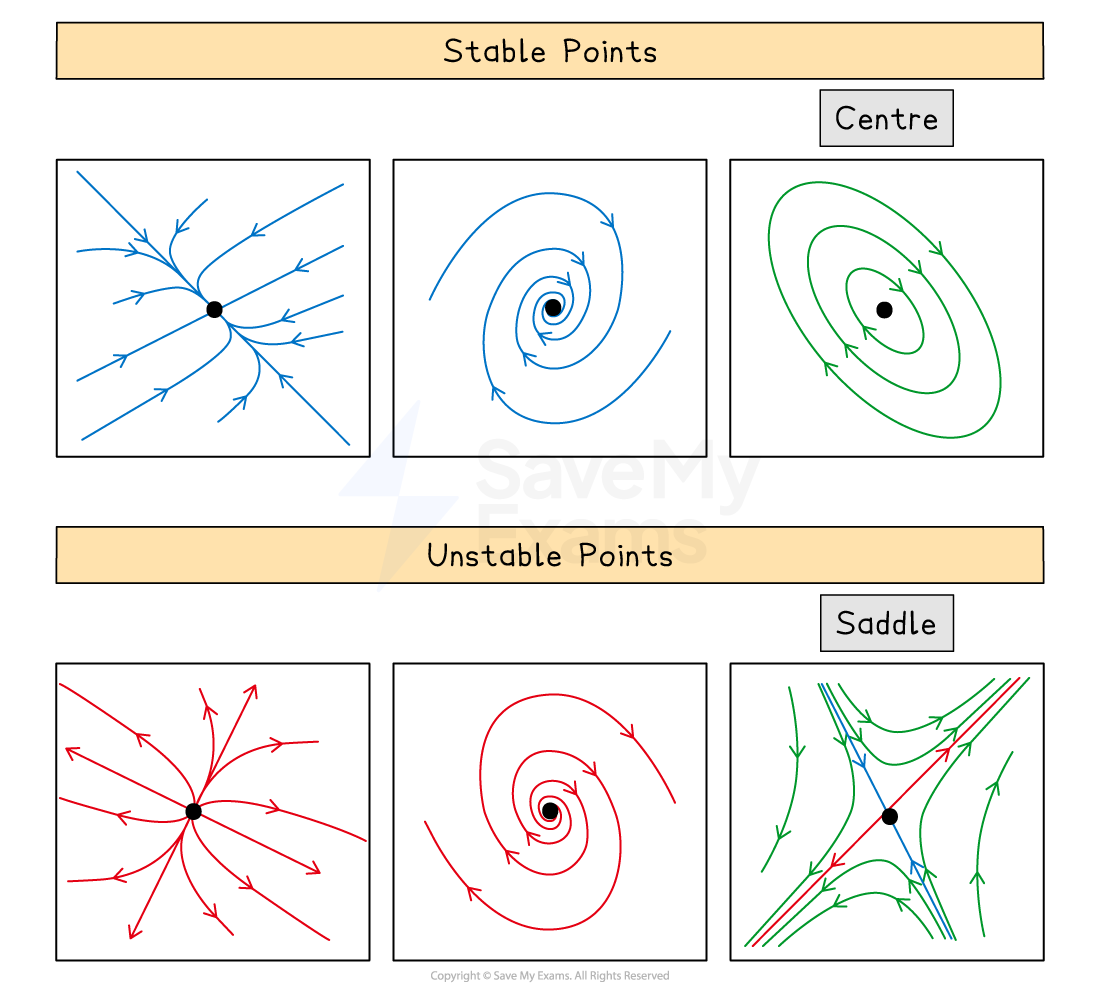
Diagram showing stable points with blue arrows and spirals, unstable points with red arrows and spirals, and a saddle point with intersecting lines.
Examples of stable and unstable equilibrium points

How can I determine the nature of an equilibrium point?

  • You can use a phase portrait to determine the nature of the equilibrium point

  • The origin left parenthesis 0 comma space 0 right parenthesis is always an equilibrium point bold italic x with dot on top equals bold italic M bold italic x, where

    • bold italic x with bold dot on top equals open parentheses table row cell x with dot on top end cell row cell y with dot on top end cell end table close parentheses

    • bold italic M equals open parentheses table row a b row c d end table close parentheses

    • bold italic x equals open parentheses table row x row y end table close parentheses

Eigenvalues of bold italic M

Nature of equilibrium point at open parentheses 0 comma space 0 close parentheses

Both positive and distinct

Unstable

Both negative and distinct

Stable

One positive and one negative

Unstable (a saddle point)

Complex with positive real parts

Unstable

Complex with negative real parts

Stable

Complex with no real parts

Stable (a centre)

Worked Example

a) Consider the system of coupled differential equations

 fraction numerator d x over denominator d t end fraction equals 2 x minus 3 y plus 6 fraction numerator d y over denominator d t end fraction equals x plus y minus 7

Show that left parenthesis 3 comma space 4 right parenthesis is an equilibrium point for the system.

5-7-1-ib-ai-hl-equilibrium-points-a-we-solution

b) Consider the system of coupled differential equations

fraction numerator d x over denominator d t end fraction equals x plus 3 y fraction numerator d y over denominator d t end fraction equals 2 x plus 2 y

Given that 4 and negative 1 are the eigenvalues of the matrix open parentheses table row 1 3 row 2 2 end table close parentheses, with corresponding eigenvectors open parentheses table row 1 row 1 end table close parentheses and open parentheses table row cell negative 3 end cell row 2 end table close parentheses, determine the coordinates and nature of the equilibrium point for the system.

5-7-1-ib-ai-hl-equilibrium-points-b-we-solution

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Phase PortraitsNext:Sketching Solution Trajectories
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.