Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes5. CalculusCoupled & Second Order Differential EquationsPhase Portraits

Phase Portraits (DP IB Applications & Interpretation (AI)): Revision Note

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

DP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): HL

Phase portraits

What is a phase portrait for a system of coupled differential equations?

  • Consider the system of coupled equations that can be represented in the matrix form bold italic x with bold dot on top equals bold italic M bold italic x, where

    • bold italic x with bold dot on top equals open parentheses table row cell x with dot on top end cell row cell y with dot on top end cell end table close parentheses

    • bold italic M equals open parentheses table row a b row c d end table close parentheses

    • bold italic x equals open parentheses table row x row y end table close parentheses

  • A phase portrait is a diagram showing how the values of x and y change over time

    • On a phase portrait we will usually sketch several typical solution trajectories

    • The precise trajectory that the solution for a particular system will travel along is determined by the initial conditions for the system

  • Suppose for the matrix bold italic M

    • lambda subscript 1 and lambda subscript 2 are the eigenvalues

    • bold italic p subscript 1 and bold italic p subscript 2 are the corresponding eigenvectors

  • The overall nature of the phase portrait depends in large part on the values of lambda subscript 1 and lambda subscript 2

Examiner Tips and Tricks

You need to know how phase portraits looks when the eigenvalues or:

  • real, distinct and non-zero

  • complex conjugates

What does the phase portrait look like when the eigenvalues are real numbers?

  • The phase portraits when the eigenvalues are real always include two lines representing the eigenvectors

    • These go through the origin

    • They are parallel to the eigenvectors

  • The origin separates these two lines into four solution trajectories

  • For example, if bold italic p subscript 1 equals open parentheses table row 1 row 2 end table close parentheses and bold italic p subscript 2 equals open parentheses table row cell negative 3 end cell row 4 end table close parentheses are eigenvectors

    • then these lines have the equations y equals 2 x and y equals negative 4 over 3 x respectively

  • The origin separates these two lines into four solution trajectories

    • Their directions depend on the signs of the corresponding eigenvalues

      • If an eigenvalue is positive then the corresponding lines are directed away from the origin

      • If an eigenvalue is negative then the corresponding lines are directed towards the origin

  • The solution trajectories have the properties:

    • As t rightwards arrow negative infinity, the solution trajectory is parallel to the line corresponding to the smaller eigenvalue

    • As t rightwards arrow infinity, the solution trajectory is parallel to the line corresponding to the larger eigenvalue

    • A solution trajectory never crosses a line corresponding to an eigenvector

Examiner Tips and Tricks

Remember that the exact solution is of the form bold italic x equals A straight e to the power of lambda subscript 1 t end exponent bold italic p subscript 1 bold plus B straight e to the power of lambda subscript 2 t end exponent bold italic p subscript bold 2 when the eigenvalues are real, distinct and non-zero. You can use this to help you determine the trajectory.

For example, consider bold italic x equals A straight e to the power of 5 t end exponent bold italic p subscript 1 bold plus B straight e to the power of 3 t end exponent bold italic p subscript bold 2.

When t less than 0 , straight e to the power of 5 t end exponent less than straight e to the power of 3 t end exponent. Therefore, as t rightwards arrow negative infinity comma space bold italic x rightwards arrow B straight e to the power of 3 t end exponent bold italic p subscript 2.

When t greater than 0 , straight e to the power of 5 t end exponent greater than straight e to the power of 3 t end exponent. Therefore, as t rightwards arrow infinity comma space bold italic x rightwards arrow A straight e to the power of 5 t end exponent bold italic p subscript 1.

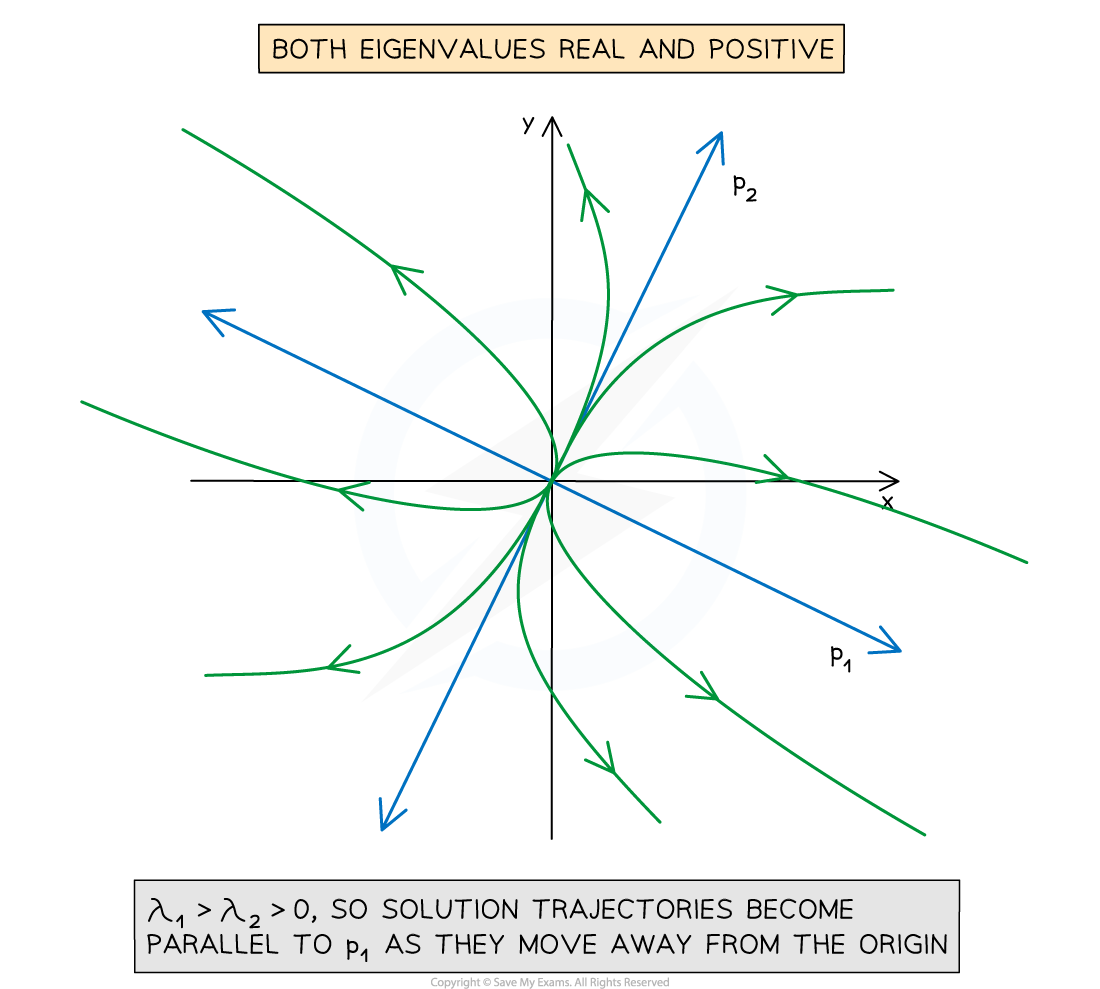
Both eigenvalues are positive

  • Suppose lambda subscript 1 greater than lambda subscript 2 greater than 0

  • All solution trajectories are directed away from the origin as t increases

  • To draw a solution trajectory

    • Start at the origin

    • Draw a line roughly parallel to bold italic p subscript 2

    • Move away from the origin and bold italic p subscript 2

    • Draw a line roughly parallel to bold italic p subscript 1

    • The line does not end

Graph showing positive eigenvalues with arrows representing solution trajectories diverging from the origin along axes labelled p1 and p2.
Example of a phase portrait when the eigenvalues are both positive

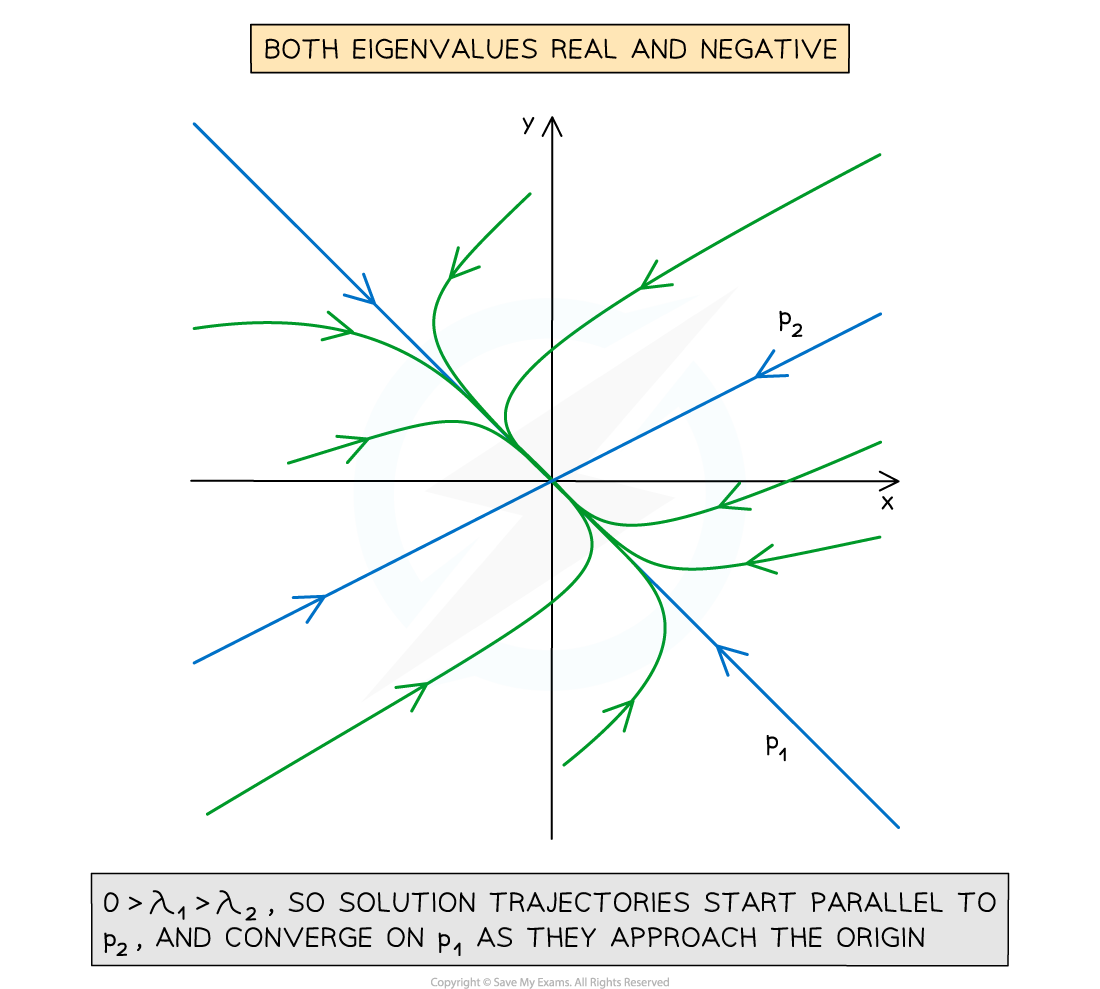
Both eigenvalues are negative

  • Suppose 0 greater than lambda subscript 1 greater than lambda subscript 2

  • All solution trajectories are directed towards the origin as t increases

  • To draw a solution trajectory

    • Start from somewhere at the edge of the graph

    • Draw a line roughly parallel to bold italic p subscript 2

    • Move toward the origin and away from bold italic p subscript 2

    • Draw a line roughly parallel to bold italic p subscript 1

    • End at the origin

Phase portrait showing trajectories with real negative eigenvalues, converging towards the origin along axis P1, diverging slightly from P2.
Example of a phase portrait when the eigenvalues are both negative

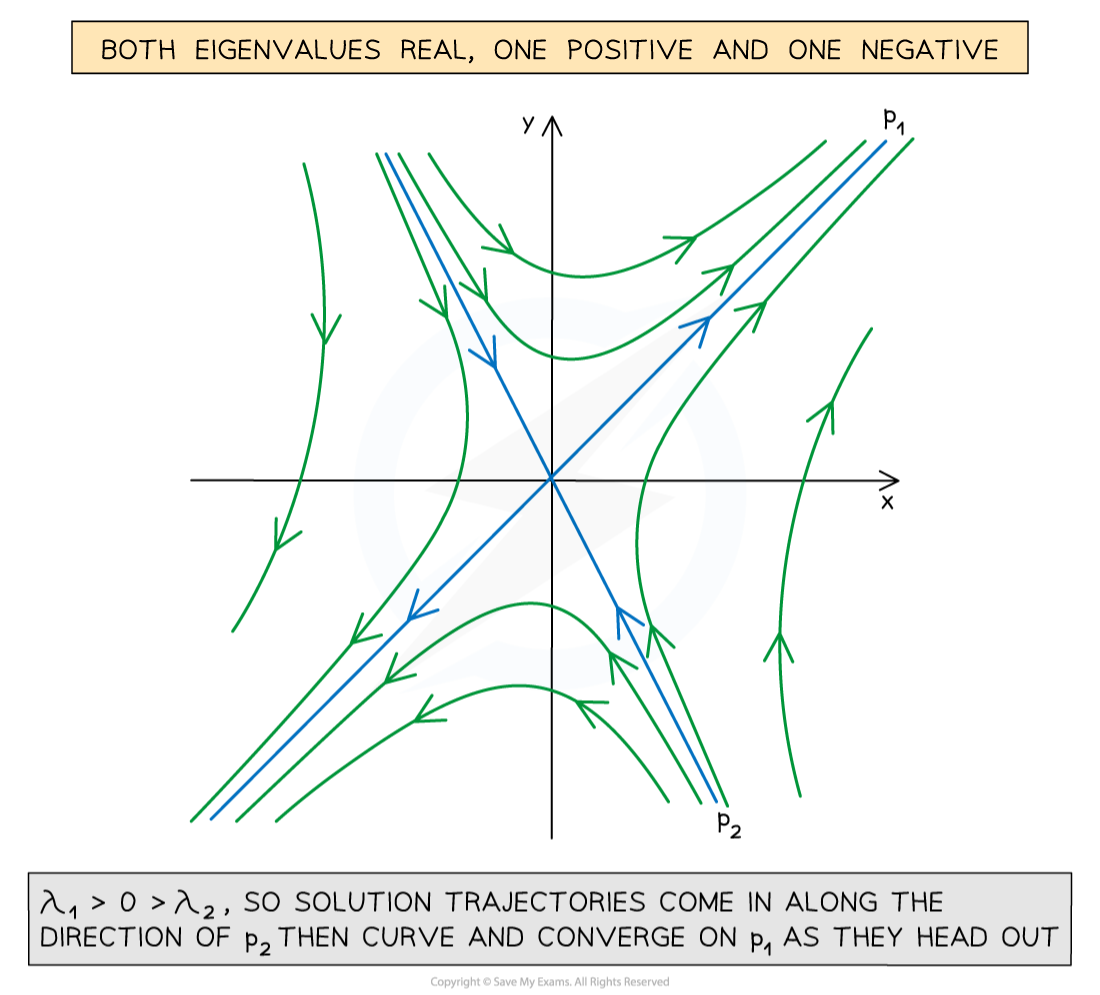
One positive and one negative eigenvalue

  • Suppose lambda subscript 1 greater than 0 greater than lambda subscript 2

  • To draw a solution trajectory

    • Start from somewhere at the edge of the graph

    • Draw a line roughly parallel to bold italic p subscript 2

    • Move toward the origin and away from bold italic p subscript 2

    • Move away from the origin and toward bold italic p subscript 1

    • Draw a line roughly parallel to bold italic p subscript 1

    • The line does not end

Phase portrait showing trajectories with real eigenvalues, one positive, one negative. Arrows enter along p2, curve, then exit along p1.
Example of a phase portrait when the eigenvalues have different signs

What does the phase portrait look like when the eigenvalues are complex numbers?

  • The phase portraits when the eigenvalues are complex always include curves orbiting the origin

    • They could be closed ellipses

    • They could be open spirals

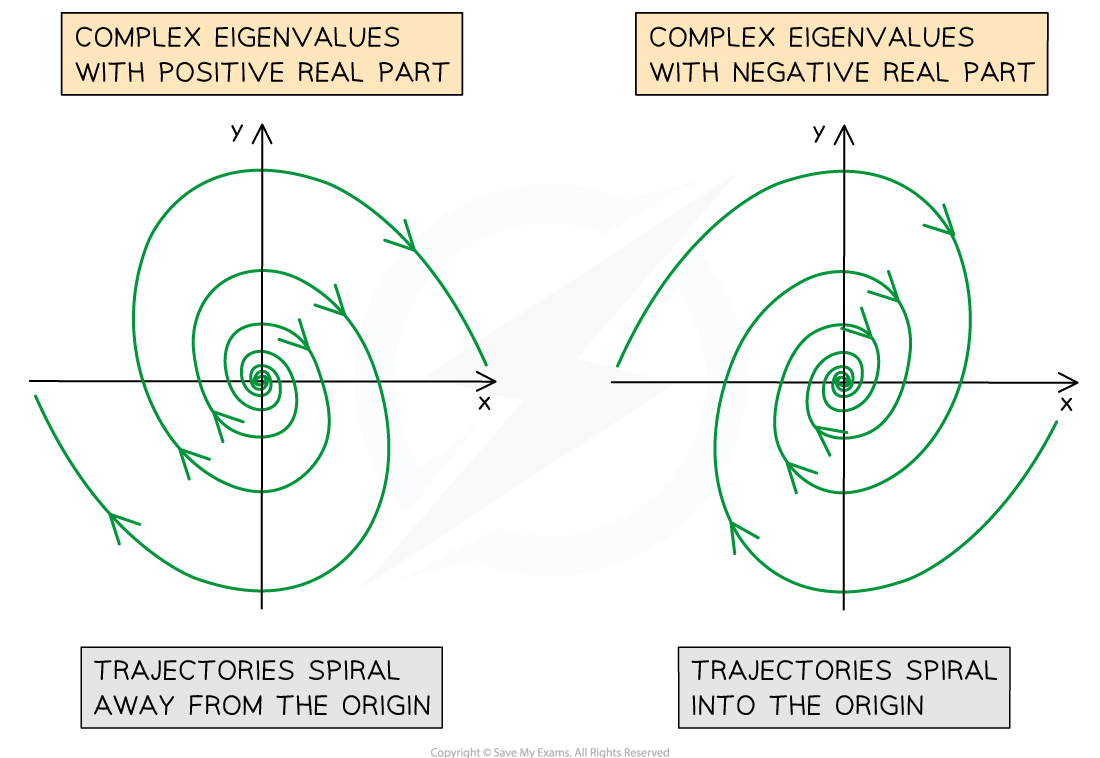
  • The real part of the complex eigenvalues affect the shape

    • Positive real parts cause the trajectories to spiral away from the origin

    • Negative real parts cause the trajectories to spiral towards the origin

    • Zero real parts cause the trajectories to form ellipses centred at the origin

  • You can find the orientation of the trajectory by finding the value of open parentheses table row cell x with dot on top end cell row cell y with dot on top end cell end table close parentheses at a specific point on one of the coordinate axes

    • For example, consider the system bold italic x with bold dot on top equals open parentheses table row 1 cell negative 2 end cell row 1 cell negative 1 end cell end table close parentheses bold italic x

      • Pick the point open parentheses 1 comma space 0 close parentheses

      • bold italic x with bold dot on top equals open parentheses table row 1 cell negative 2 end cell row 1 cell negative 1 end cell end table close parentheses open parentheses table row 1 row 0 end table close parentheses equals open parentheses table row 1 row 1 end table close parentheses

      • From open parentheses 1 comma space 0 close parentheses, the trajectory is moving to the right and up

      • Therefore, it is counter-clockwise around the origin

Examiner Tips and Tricks

To make it easiest, you should pick open parentheses 1 comma space 0 close parentheses or open parentheses 0 comma space 1 close parentheses.

The trajectory is clockwise if it is moving down from open parentheses 1 comma space 0 close parentheses or right from open parentheses 0 comma space 1 close parentheses.

Real part is equal to zero

  • Suppose lambda subscript 1 equals b straight i and lambda subscript 2 equals negative b straight i

  • To draw a solution trajectory

    • Find the direction at open parentheses 1 comma space 0 close parentheses or open parentheses 0 comma space 1 close parentheses to determine if it is clockwise or counter-counter

    • Draw ellipses that are centred at the origin

Graph of concentric elliptical trajectories around origin with arrows indicating anticlockwise direction; labelled "Purely Imaginary Eigenvalues".
Example of a phase portrait when the real part of the complex eigenvalues is zero

Real part is not equal to zero

  • Suppose lambda subscript 1 equals a plus b straight i and lambda subscript 2 equals a minus b straight i

  • To draw a solution trajectory

    • Find the direction at open parentheses 1 comma space 0 close parentheses or open parentheses 0 comma space 1 close parentheses to determine if it is clockwise or counter-counter

    • Draw spirals from origin

    • Label the direction of the trajectories

      • If a less than 0 it spirals towards the origin

      • If a greater than 0 it spirals away from the origin

Diagram comparing complex eigenvalues; left with positive real part spirals outwards, right with negative real part spirals inwards.
Example of phase portraits when the real part of the complex eigenvalues is not zero

Worked Example

Consider the system of coupled differential equations

 fraction numerator d x over denominator d t end fraction equals negative 2 x plus 2 y fraction numerator d y over denominator d t end fraction equals x minus 3 y

Given that negative 1 and negative 4 are the eigenvalues of the matrix open parentheses table row cell negative 2 end cell 2 row 1 cell negative 3 end cell end table close parentheses, with corresponding eigenvectors open parentheses table row 2 row 1 end table close parentheses and open parentheses table row cell negative 1 end cell row 1 end table close parentheses, draw a phase portrait for the solutions of the system.

5-7-1-ib-ai-hl-phase-portraits-we-solution

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Coupled Differential EquationsNext:Equilibrium Points
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.