Truth Tables (Cambridge (CIE) IGCSE Computer Science): Revision Note

Truth Tables

What is a truth table?

• A truth table is a tool used in logic and computer science to visualise the results of Boolean expressions

• They represent all possible inputs and the associated outputs for a given Boolean expression

AND 

Circuit symbol	Truth Table
	A B A AND B 0 0 0 0 1 0 1 0 0 1 1 1

OR

Circuit symbol	Truth Table
	A B A OR B 0 0 0 0 1 1 1 0 1 1 1 1

NOT

Circuit symbol	Truth Table
	A NOT 0 1 1 0

XOR (exclusive)

Circuit symbol	Truth Table
	A B A XOR B 0 0 0 0 1 1 1 0 1 1 1 0

NAND (not and)

Circuit symbol	Truth Table
	A B NOT (A AND B) 0 0 1 0 1 1 1 0 1 1 1 0

NOR (not or)

Circuit symbol	Truth Table
	A B NOT (A OR B) 0 0 1 0 1 0 1 0 0 1 1 0

Truth Tables for Logic Circuits

How do you create truth tables for logic circuits?

• To create a truth table for the expression P = (A AND B) AND NOT C 

  • Calculate the numbers of rows needed (2^{number of inputs})

  • In this example there are 3 inputs (A, B, C) so a total of 8 rows are needed (2³)

  • To not miss any combination of inputs, start with 000 and count up in 3-bit binary (0-7)

• Add a new column to show the results of the brackets first (A AND B)

• Add a new column to show the results of NOT C

• The last column shows the result of the Boolean expression (P) by comparing (A AND B) AND NOT C // 

How do you create logic circuits from a truth table?

• To create a logic circuit from a truth table you need to:

  • Find the rows where the output = 1

  • Build a logic branch for each of the rows

  • Combine the branches

  • Determine the gates needed

  • Construct a logic expression

  • Create the logic circuit

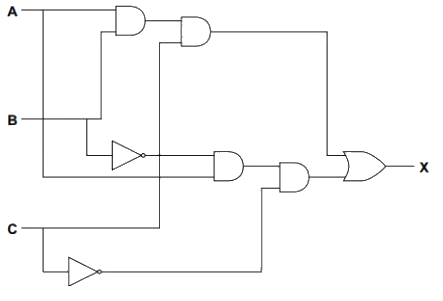
Example

• Look at the truth table and find the rows where X = 1

• This happens when:

  • A = 1, B = 0, C = 0

  • A = 1, B = 1, C = 1

• Build a logic branch:

  • A = 1, B = 0, C = 0

    • Use a NOT gate on B

    • Use a NOT gate on C

    • AND A, NOT B, and NOT C together

    • This gives output = 1 for that row

  • A = 1, B = 1, C = 1

    • Just AND A, B, and C together

• Combine the branches

  • Use an OR gate to combine the two outputs

    • This way, X = 1 if either input combination happens

• Determine the gates needed:

  • NOT gates:

    • NOT B

    • NOT C

  • AND gates:

    • A AND NOT B → first AND

    • that result AND NOT C → second AND

    • A AND B → third AND

    • that result AND C → fourth AND

  • OR gate:

    • Combines the outputs of the second and fourth AND gates

• Construct the logic expression

  • Final logic:

    • (A AND NOT B AND NOT C) OR (A AND B AND C)

• Create the logic circuit