Area Between a Curve and a Line (DP IB Analysis & Approaches (AA)): Revision Note

Area Between a Curve and a Line

• Areas whose boundaries include a curve and a (non-vertical) straight line can be found using integration

  • For an area under a curve a definite integral will be needed

  • For an area under a line the shape formed will be a trapezium or triangle

    • basic area formulae can be used rather than a definite integral

    • using a GDC, one method is not particularly trickier than the other

• The total area required could be the sum or difference of the area under the curve and the area under the line

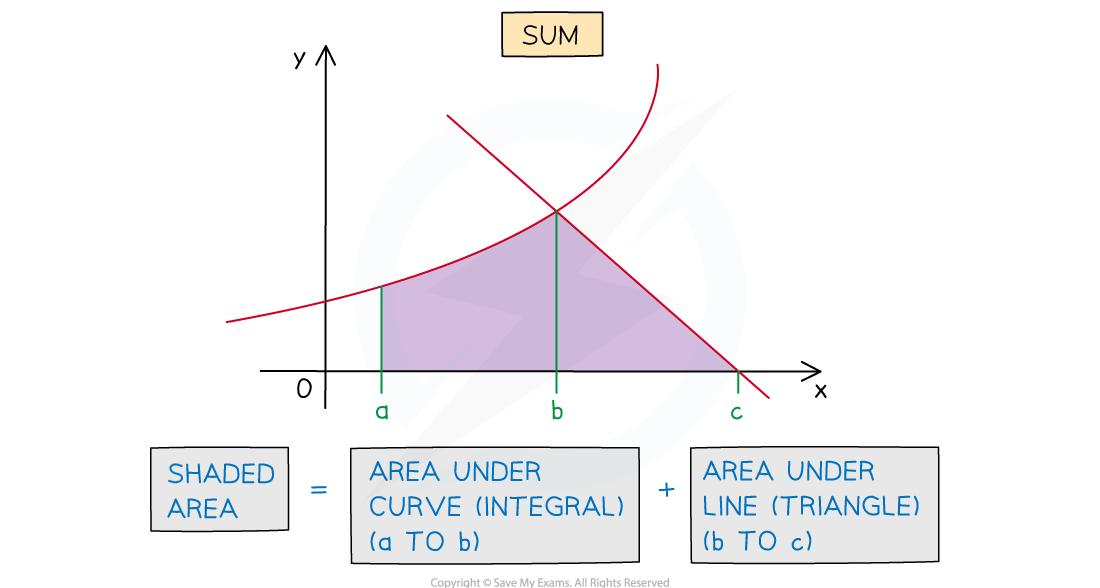
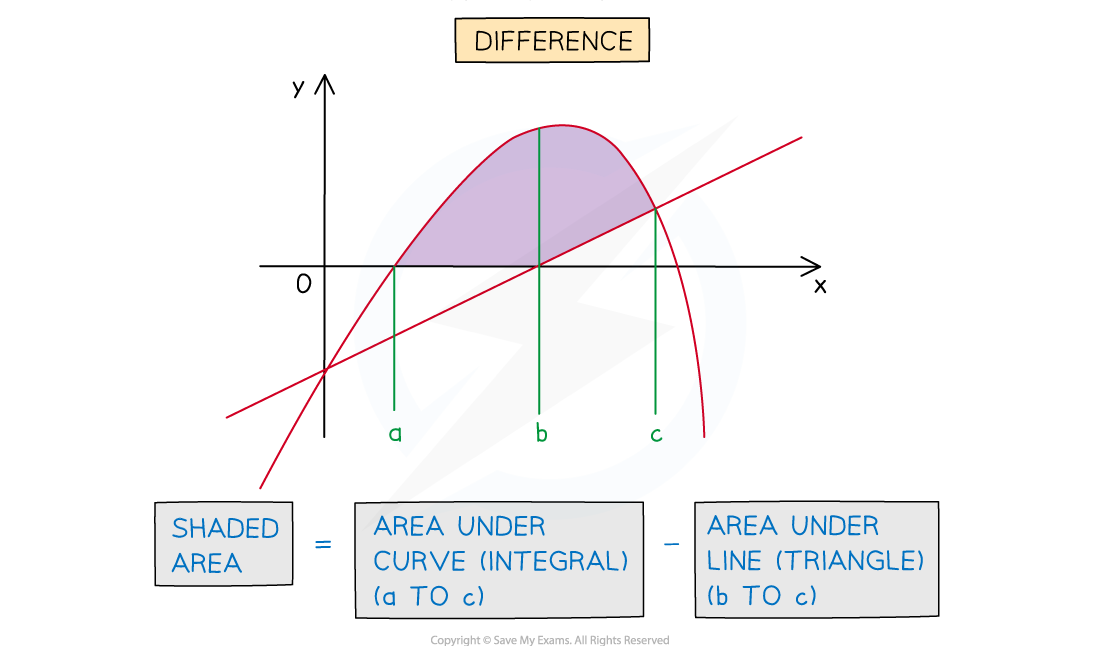
How do I find the area between a curve and a line?

STEP 1

If a diagram is not given, use a GDC to draw the graphs of the curve and line and identify the area to be found

STEP 2

Use a GDC to find the root(s) of the curve, the root of the line, and the x-coordinates of any intersections between the curve and the line.

STEP 3

Use the graph to determine whether areas will need adding or subtracting

Deduce the limits and thus the definite integral(s) to find the area(s) under the curve and the line
Use a GDC to calculate the area under the curve

Remember to include the modulus (|...|) symbols around the function

Use a GDC to calculate the area under the line - this could be another definite integral or for a triangle or for a trapezium

STEP 4

Add or subtract areas accordingly to obtain a final answer