Graphing Functions & Their Key Features (DP IB Analysis & Approaches (AA)): Revision Note

Graphing functions

How do I sketch the graph of y = f(x)?

• The function can be sketched using the equation

  • where

    • the -axis shows the inputs (domain)

    • the -axis shows the outputs (range)

  • e.g. if then is a point on the graph

• You could be asked to sketch the sum or difference of two functions

  • Use your GDC to plot or 

What is the difference between“sketch” and “draw”?

• If asked to sketch then you need to create an image that includes

  • the coordinate axes

    • labelled and

  • the general shape of a curve

    • drawn freehand

    • this does not have to be exact

  • key points labelled with coordinates

    • e.g. points of intersections with axes

• If asked to draw then you need to

  • use a pencil and ruler

  • draw to scale

  • add labelled axes

  • plot any points accurately

    • you may need a table of values

  • join points with a straight line or smooth curve

How do I use my GDC to help sketch a graph?

• First use your GDC to plot the graph

  • then find any key points

    • including their coordinates

  • then create a sketch of the graph shown on the GDC screen

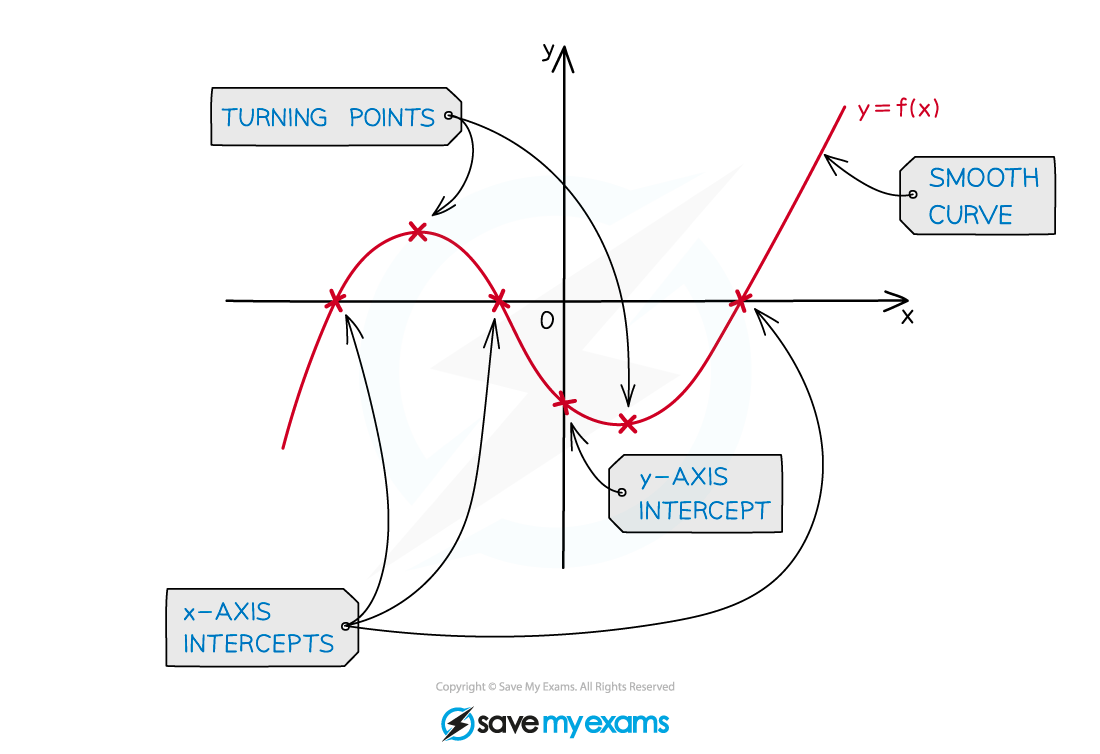
Key features of graphs

What are the key features of graphs?

• You should be familiar with the following key features and know how to use your GDC to find them

• Local minimums/maximums

  • Also called turning points

    • where the graph changes its direction between upwards and downwards

  • A graph can have multiple local minimums/maximums

    • A local minimum/maximum is not necessarily the minimum/maximum of the whole graph

    • This would be called the global minimum/maximum

  • For quadratic graphs the minimum/maximum is called the vertex

• Intercepts

  • ­­ – intercepts are where the graph crosses the -axis

    • At these points

  • – intercepts are where the graph crosses the -axis

    • At these points

  • These points are also called the zeros of the function

    • or roots of the equation

• Symmetry

  • Some graphs have symmetry

    • e.g. a quadratic has a vertical line of symmetry

• Asymptotes

  • These are lines which the graph will get closer to but not cross

    • These can be horizontal or vertical

  • Exponential graphs have horizontal asymptotes

    • e.g. has the asymptote

  • Reciprocal graphs have horizontal and vertical asymptotes

    • e.g. has the asymptotes and