Minimum Spanning Trees (Prim's Algorithm) (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Prim's algorithm
How can I use Prim’s algorithm to find a minimum spanning tree?
STEP 1
Start at any vertex and choose the nearest adjacent vertexSTEP 2
Choose the nearest adjacent vertex to any of the currently selected verticesYou do not need to only look at the last selected vertex
You can look at all the selected vertices
STEP 3
Repeat step 2 until all the vertices are added to the tree
Examiner Tips and Tricks
Make sure you state the order of your selected vertices. The question might ask you to state the edges.
Worked Example
Consider the weighted graph below.
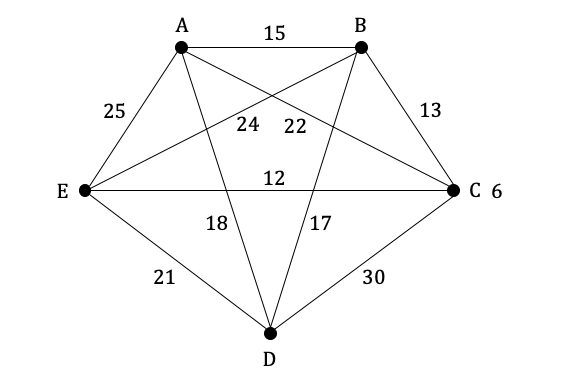
a) Using Prim’s algorithm, find the minimum spanning tree.
Answer:

b) State the total weight of the minimum spanning tree.
Answer:

Prim's algorithm using a matrix
How do I apply Prim’s algorithm to a weighted adjacency table?
STEP 1
Select any vertex to start fromCross out the values in the column associated with that vertex
Label the row associated with the vertex 1
STEP 2
Circle the lowest value in any cell along that row and add the corresponding edge to your treeCross out the remaining values in the column of the cell that you have circled
Label the row associated with the last selected vertex with the next number
STEP 3
Circle the lowest value in any cell along any of the rows that have been labelled and add the edge to your treeCross out the remaining values in the column of the cell that you have circled
Label the row associated with the last selected vertex with the next number
STEP 4
Repeat step 3 until all rows have been labelled and all vertices have been added to the treeThe labels tell you the order in which you selected the vertices
Which algorithm is better for finding minimum spanning trees?
Kruskal’s algorithm can be used when the information is in graph form whereas Prim’s algorithm can be used in either graph or matrix form.
Prim’s algorithm is sometimes considered to be more efficient than Kruskal’s algorithm because
the edges do not need to be ordered at the start and
it does not rely on checking for cycles at each step
An exam question will usually specify which method should be used, otherwise you have the choice
If you are asked to find the minimum spanning tree and the information given in the question is in the form of a table, you should use Prim’s algorithm
Examiner Tips and Tricks
Look out for questions that ask you to minimise the cost or length etc. from a weighted graph – they are implying that they want you to find the minimum spanning tree!
Worked Example
Celeste is building a model city incorporating 6 main buildings that need to be connected to an electrical supply.
Each vertex listed in the table below represents a building and the weighting of each edge is the cost in USD of creating a link to the electrical supply between the given vertices.
| A | B | C | D | E | F |
|---|---|---|---|---|---|---|
A | - | 4 | 9 | 8 | 11 | 3 |
B | 4 | - | 13 | 2 | 5 | 12 |
C | 9 | 13 | - | 7 | 1 | 4 |
D | 8 | 2 | 7 | - | 10 | 3 |
E | 11 | 5 | 1 | 10 | - | 15 |
F | 3 | 12 | 4 | 3 | 15 | - |
Celeste wants to find the lowest cost solution that links all 6 buildings up to the electrical supply.
a) Starting from vertex A, use Prim’s algorithm on the table to find and draw the minimum spanning tree. Show each step of the process clearly.
Answer:


b) State the lowest cost of connecting all of the buildings to the electricity supply.
Answer:


Unlock more, it's free!
Was this revision note helpful?