Quadratic Inequalities (Cambridge (CIE) IGCSE Additional Maths): Revision Note
Exam code: 606
Did this video help you?
Quadratic inequalities
What are quadratic inequalities?
They are similar to quadratic equations with the "=" replaced by one of <, >, ≤ or ≥
Just like equations such inequalities should be in a form such that 0 is on one side of the inequality
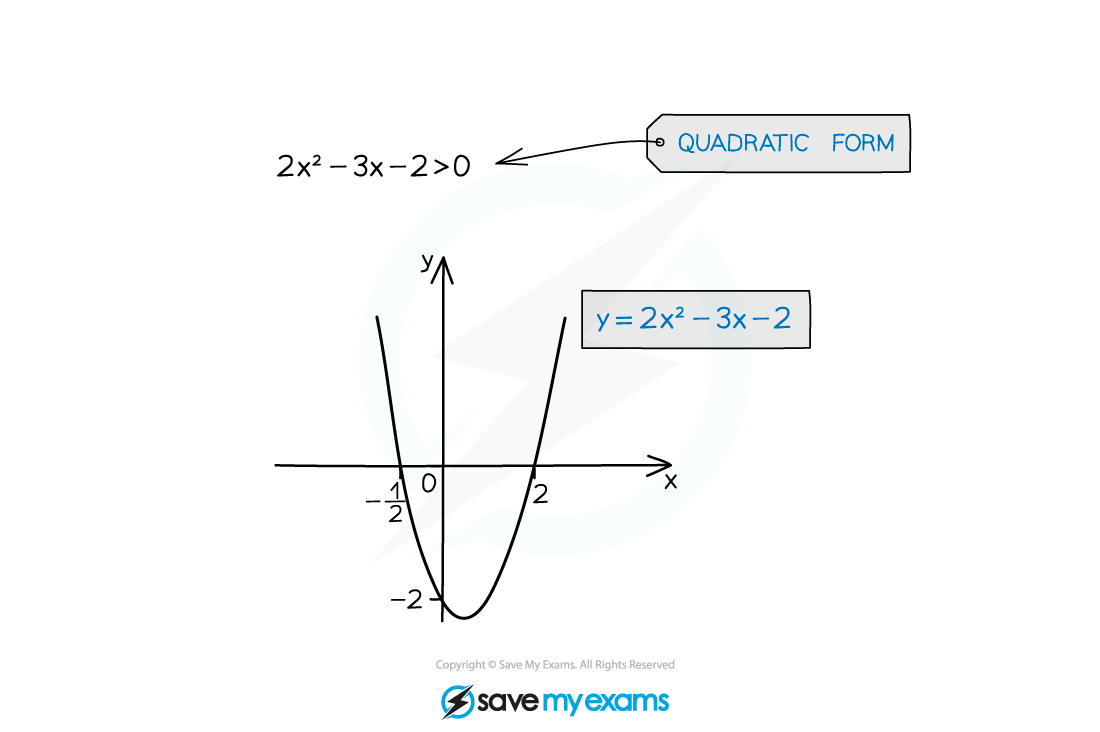
e.g.
Sketching a quadratic graph is essential to finding the correct solution(s)
Some modern calculators may be able to solve quadratic inequalities directly
You could use this to check your answer
How do I solve quadratic inequalities?
STEP 1
Rearrange the inequality into quadratic form with a positive squared term ax2 + bx + c > 0 (>, <, ≤ or ≥)STEP 2
Find the roots of the quadratic equation Solve ax2 + bx + c = 0 to get x1 and x2 where x1 ≤ x2STEP 3
Sketch the graph of the quadratic and label the roots As Step 1 makes the-squared term positive it will be
-shaped
STEP 4
Identify the region that satisfies the inequality For ax2 + bx + c > 0 you want the region above the x-axis - the solution will be x < x1 or x > x2 For ax2 + bx + c < 0 you want the region below the x-axis - the solution will be x1 < x < x2
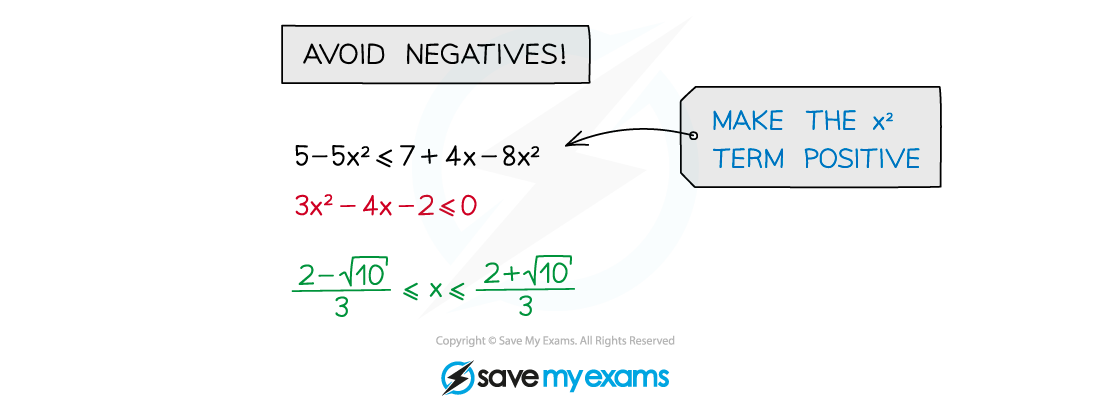
Be careful:
avoid multiplying or dividing by a negative number
if unavoidable, “flip” the inequality sign so < → >, ≥ → ≤, etc
do rearrange to make the x2 term positive
Quadratic inequalities and the discriminant
The discriminant of the quadratic function
is
It's value indicates the number of (real) roots the quadratic function has
if
there are two roots
if
there is one root (repeated)
if
there are no roots
The firsts and last of these are quadratic inequalities
Some questions will require you to use the discriminant to set up and solve a quadratic inequality
For example: Find the values of
such that the equation
has no real roots
Using the discriminant, and for no real roots,
Using the approach above, this leads to the quadratic inequality in
,
And using the method above, including sketching a graph, leads to the solutions
and
Examiner Tips and Tricks
Some calculators will solve quadratic inequalities directly and just give you the answer
Beware!
make sure you have typed the inequality in correctly
the calculator may not display the answer in a conventional way
e.g
may be shown as
Both are mathematically correct but the first way is how it would normally be written
these questions could crop up on the non-calculator exam paper
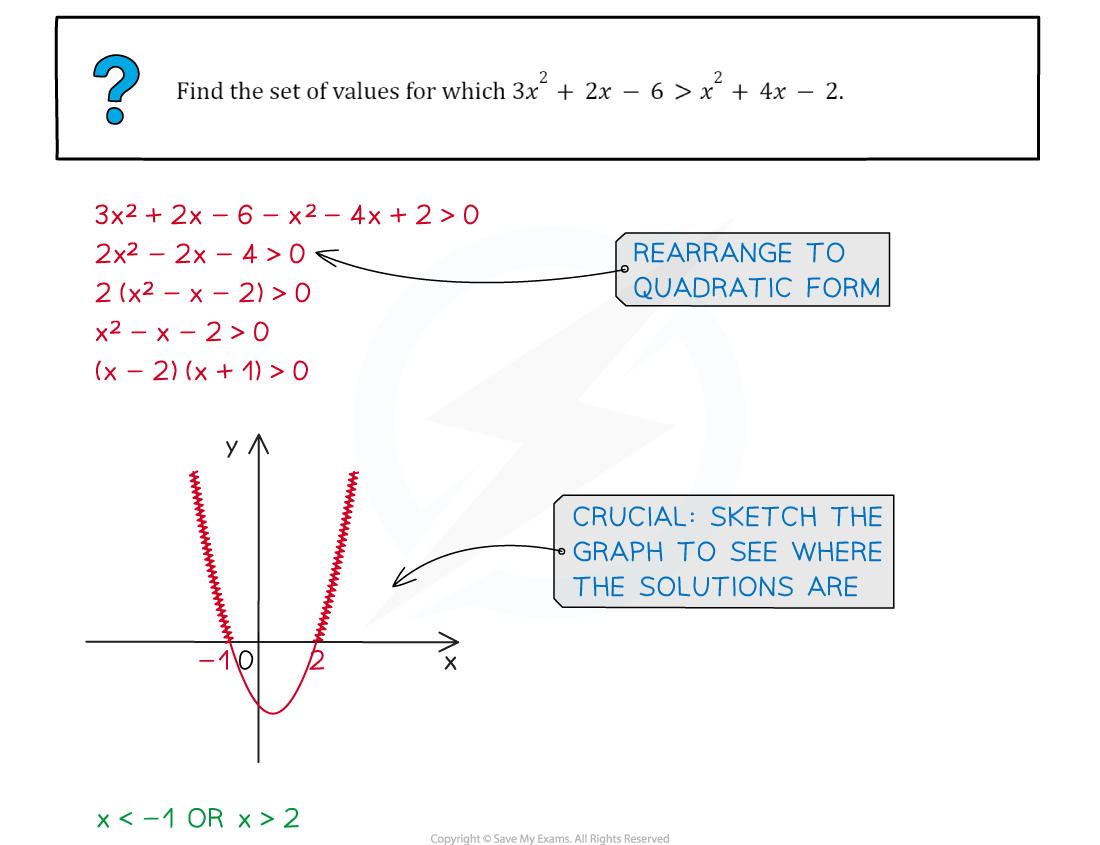
Worked Example
Did this video help you?
Inequalities on graphs
What are inequalities on graphs?
Inequalities can be represented on graphs by shaded regions and dotted or solid lines
These inequalities have two variables, x and y
Several inequalities are used at once
The solution is an area on a graph (often called a region and labelled R)
The inequalities can be linear or quadratic

How do I draw inequalities on a graph?
Sketch each line or curve
If the inequality is strict (< or >) then use a dotted line
If the inequality is weak (≤ or ≥) then use a solid line
Decide which side of the line satisfies the inequality
If unsure, choose a coordinate on one side and test it in the inequality
The origin is an easy point to use
If it satisfies the inequality then that whole side of the line satisfies the inequality
For example: (0,0) satisfies the inequality y < x2 + 1 so you want the side of the curve that contains the origin

Examiner Tips and Tricks
Recognise this type of inequality by the use of two variables
You may have to deduce the inequalities from a given graph
Pay careful attention to which region you are asked to shade
Sometimes the exam could ask you to shade the region that satisfies the inequalities this means you should shade the region that is wanted.
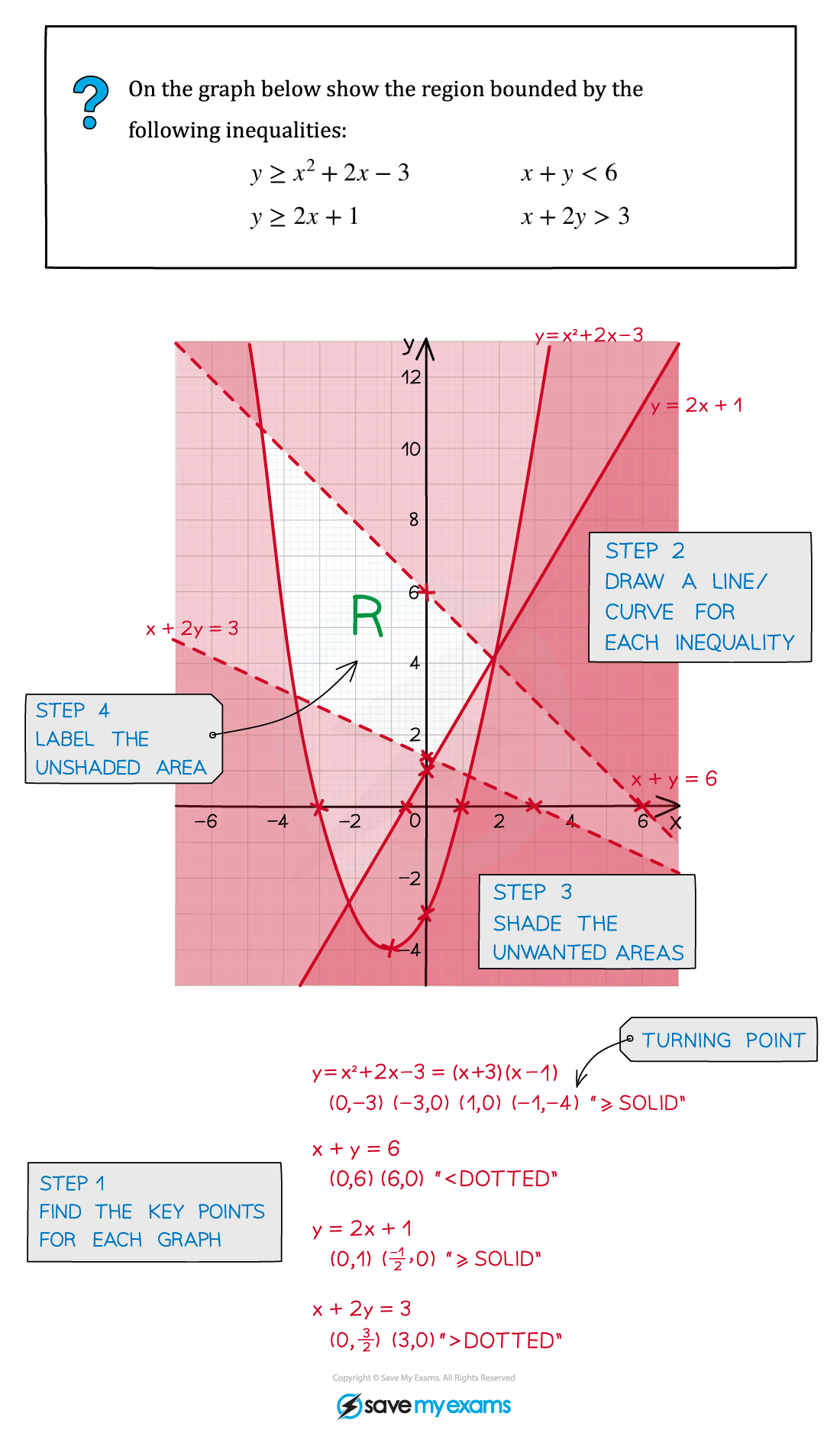
Worked Example

Unlock more, it's free!
Did this page help you?