Viscous Drag (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Stoke's Law
Viscous drag
Viscous drag is defined as:
The frictional force between an object and a fluid which opposes the motion between the object and the fluid
The viscous drag on a small sphere can be calculated using Stokes’ law:
Where
F = viscous drag force (N)
η = coefficient of viscosity of the fluid (N s m−2 or Pa s)
r = radius of the object (m)
v = velocity of the object (m s−1)
The viscosity of a fluid can be thought of as its thickness, or how much it resists flowing
Fluids with low viscosity are easy to pour, while those with high viscosity are difficult to pour
The coefficient of viscosity is a property of the fluid (at a given temperature) that indicates how much it will resist flow
The rate of flow of a fluid is inversely proportional to the coefficient of viscosity
Terminal velocity of a sphere in a fluid
When an object falls through a fluid (e.g. a skydiver falling through the air), it reaches terminal velocity
This occurs when the weight of the object balances with the upthrust and the viscous drag force
weight = upthrust + viscous drag
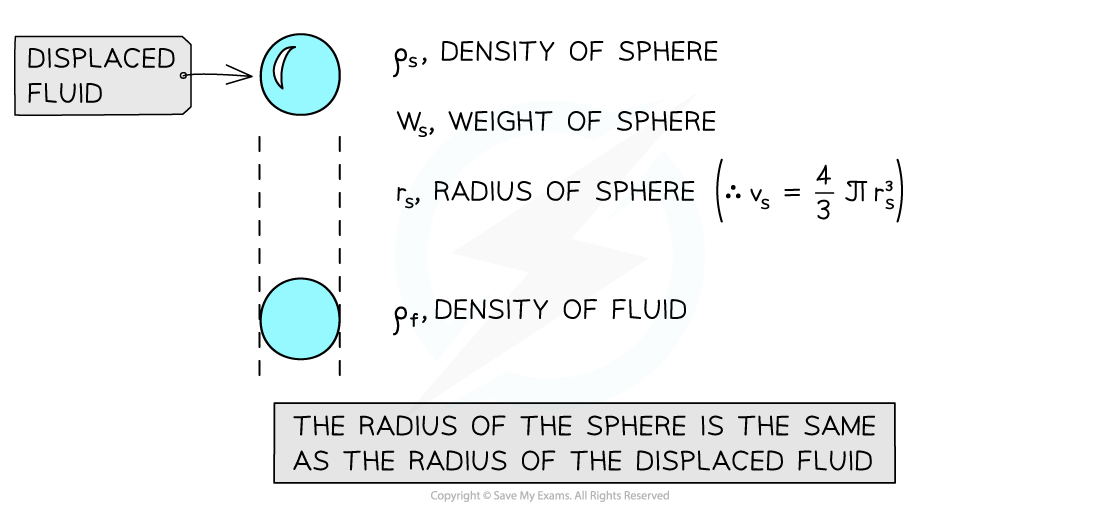
Forces acting on a sphere falling through a fluid

At terminal velocity, the forces on the sphere are balanced: W (downwards) = Fd + U (upwards)
Consider a small, solid sphere of radius
moving slowly at terminal velocity through a fluid of viscosity
The upthrust
on the sphere is equal to the weight of the fluid displaced
Where
= mass of the sphere (kg)
= mass of the fluid displaced (kg)
= acceleration due to gravity (m s−2)
= terminal velocity of the sphere (m s−1)
Using the density equation, the mass
of the sphere is given by:
Where:
= density of the sphere (kg m–3)
The volume of displaced fluid is the same as the volume of the sphere
Therefore, the mass
of displaced fluid is given by:
Where:
= density of the fluid (kg m–3)
Substituting the expressions for mass back into the original equation:
Rearrange to make terminal velocity the subject of the equation
Finally, cancel out r from the top and bottom to find an expression for terminal velocity in terms of the radius of the sphere and the coefficient of viscosity
This final equation shows that terminal velocity is:
directly proportional to the square of the radius of the sphere
inversely proportional to the viscosity of the fluid
Understanding Viscosity & Stoke's Law
Conditions for Stoke’s Law Equation
The equation can only be used when certain conditions are met:
The flow is laminar
The object is small
The object is spherical
Motion between the sphere and the fluid is at a slow speed

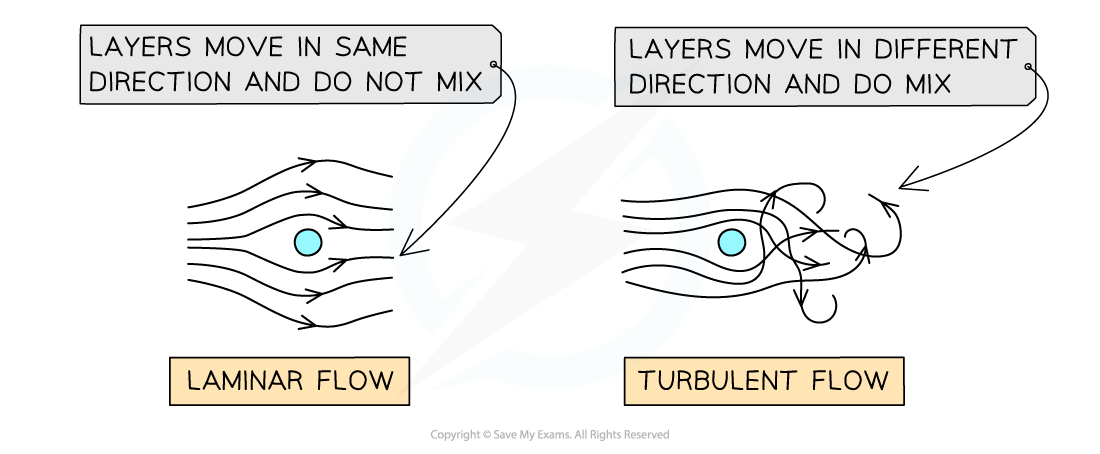
Laminar flow and turbulent flow
As an object moves through a fluid, or a fluid moves around an object, layers in the fluid are created
In laminar flow, all the layers are moving in the same direction, and they do not mix
This tends to happen for slow-moving objects or slow-flowing liquids
The equation above only applies to laminar flow
In turbulent flow, the layers move in different directions, and the layers do mix
Changing viscosity
Viscosity is temperature-dependent
Liquids are less viscous as the temperature increases
Gases get more viscous as the temperature increases
Worked Example
A ball bearing of radius 5.0 mm falls at a constant speed of 0.030 m s–1 through an oil which has a viscosity of 0.3 Pa s and a density of 900 kg m–3.
Determine the viscous drag acting on the ball bearing.
Answer:
Step 1: List the known quantities in SI units
Radius of the sphere, rs = 5.0 mm = 5.0 × 10-3 m
Terminal velocity of the sphere, v = 0.03 m s-1
Viscosity of oil, η = 0.3 Pa s
Density of oil, ρf = 900 kg m−3
Step 2: Sketch a free-body diagram to resolve the forces at constant speed
Ws = Fd + U

Step 3: Calculate the value for viscous drag, Fd
Fd = 6πηrv = 6 × π × 0.3 × 5.0 × 10-3 × 0.03 = 0.008482
Step 4: Write the complete answer to the correct significant figures and include units
The viscous drag, Fd = 8.5 × 10-4 N
Examiner Tips and Tricks
You may need to write out some or all of the derivation given in the first part above.
It is really important to keep clear whether you are talking about the density of the sphere or the fluid, and the mass of the sphere or the fluid.
Practice using subscripts, and do try this at home. It isn’t one to do for the first time in an exam!

Unlock more, it's free!
Was this revision note helpful?