Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)SLRevision Notes2. FunctionsFunctions ToolkitInverse Functions

Inverse Functions (DP IB Analysis & Approaches (AA)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Mark Curtis

Updated on

DP Analysis & Approaches (AA): SLDP Analysis & Approaches (AA): SLDP Applications & Interpretation (AI): HLDP Analysis & Approaches (AA): HL

Inverse functions

What is an inverse function?

  • An inverse function, f to the power of negative 1 end exponent open parentheses x close parentheses, reverses (or undoes) the effect of f open parentheses x close parentheses

    • for example

      • if f open parentheses x close parentheses equals 2 x then f to the power of negative 1 end exponent open parentheses x close parentheses equals x over 2

      • if g open parentheses x close parentheses equals x plus 10 then g to the power of negative 1 end exponent open parentheses x close parentheses equals x minus 10

  • Inverse functions can be used to solve equations

    • e.g. the solution of f left parenthesis x right parenthesis equals 8 is x equals f to the power of negative 1 end exponent left parenthesis 8 right parenthesis

Diagram of inverse functions showing input to output with f(x) and reverse with f⁻¹(x). Labels: "Inverse Functions", "Input", "Output".

Examiner Tips and Tricks

Note that the inverse function space f to the power of negative 1 end exponent left parenthesis x right parenthesis  is not the same as the reciprocal of the function fraction numerator 1 over denominator f open parentheses x close parentheses end fraction equals open square brackets f open parentheses x close parentheses close square brackets to the power of negative 1 end exponent.

What is the identity function?

  • The identity function id maps each value to itself

    • id left parenthesis x right parenthesis equals x

      • e.g. id open parentheses 5 close parentheses equals 5

  • Applying a function space f to an input

    • then applying the inverse, space f to the power of negative 1 end exponent 

      • gives back the original input

  • This also works if you swap the order of space f and space f to the power of negative 1 end exponent 

    • i.e. the composite function left parenthesis f ring operator f to the power of negative 1 end exponent right parenthesis left parenthesis x right parenthesis equals left parenthesis f to the power of negative 1 end exponent ring operator f right parenthesis left parenthesis x right parenthesis equals x

      • has the same effect as the identity function

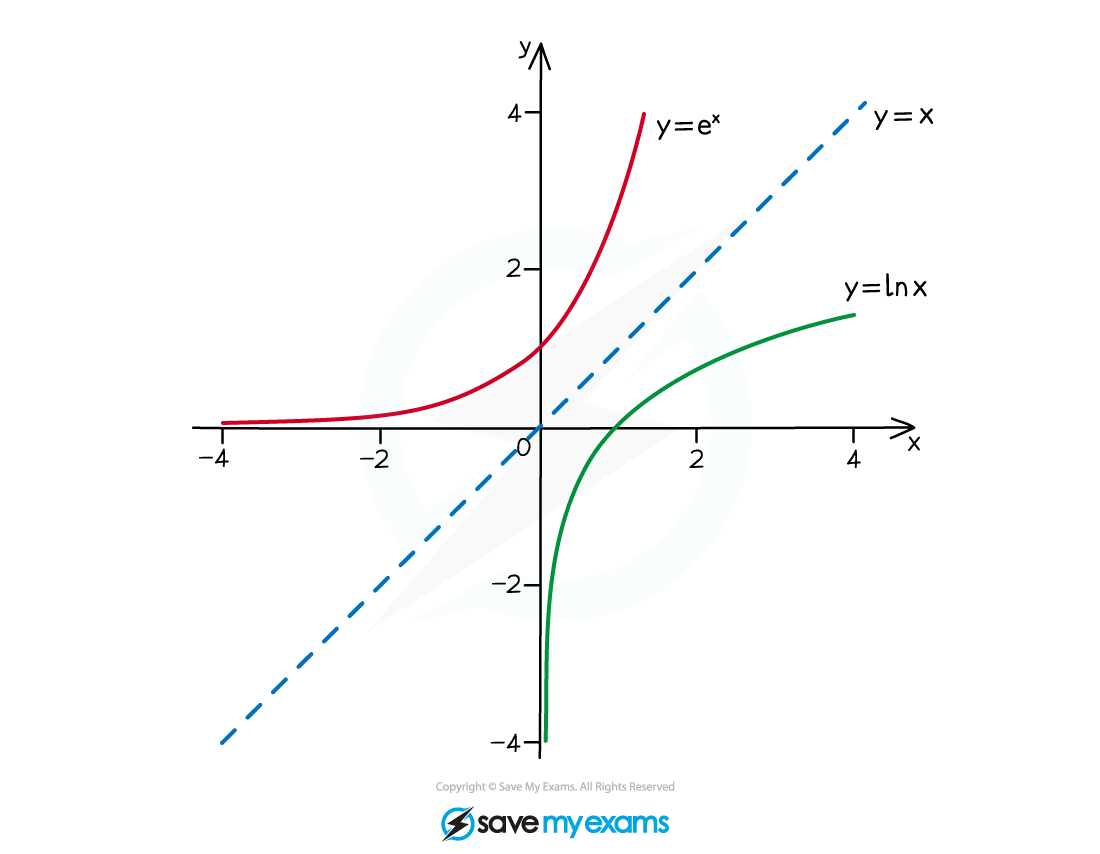
How do I sketch an inverse function?

  • The graph of space y equals f to the power of negative 1 end exponent left parenthesis x right parenthesis is a reflection of the graph space y equals f left parenthesis x right parenthesis in the line space y equals x

    • e.g. if f open parentheses x close parentheses equals 2 x and f to the power of negative 1 end exponent open parentheses x close parentheses equals x over 2

      • then y equals 2 x and y equals 1 half x

      • which reflect in y equals x

Graph depicting curves y=e^x in red and its inverse function y=ln x in green, both of which are reflections of each other about the line y=x.

  • If y equals f open parentheses x close parentheses intersects y equals x then f to the power of negative 1 end exponent open parentheses x close parentheses also intersects y equals x at the same point

    • i.e. solutions to either space f left parenthesis x right parenthesis equals x or space f to the power of negative 1 end exponent left parenthesis x right parenthesis equals x

      • are solutions to space f left parenthesis x right parenthesis equals f to the power of negative 1 end exponent left parenthesis x right parenthesis

    • There may be other solutions to space f left parenthesis x right parenthesis equals f to the power of negative 1 end exponent left parenthesis x right parenthesis that don't lie on the line space y equals x

How do I find the inverse of a function?

  • To find the inverse function using algebra, following these steps:

  • STEP 1
    Swap the x and y in space y equals f left parenthesis x right parenthesis

  • STEP 2
    Rearrange x equals f left parenthesis y right parenthesis to make space y the subject

    • The result is f to the power of negative 1 end exponent open parentheses x close parentheses

How do I find the domain and range of an inverse function?

  • The domain of a function becomes the range of its inverse

    • e.g. if f open parentheses x close parentheses equals 2 x has domain 1 less or equal than x less or equal than 3

      • then the range of f to the power of negative 1 end exponent open parentheses x close parentheses is 1 less or equal than f to the power of negative 1 end exponent open parentheses x close parentheses less or equal than 3

  • The range of a function becomes the domain of its inverse

    • e.g. if f open parentheses x close parentheses equals 2 x has range 2 less or equal than f open parentheses x close parentheses less or equal than 6

      • then the domain of f to the power of negative 1 end exponent open parentheses x close parentheses is 2 less or equal than x less or equal than 6

What condition is needed for an inverse function to exist?

  • For an inverse function f to the power of negative 1 end exponent open parentheses x close parentheses to exist

    • the original function f open parentheses x close parentheses must be one-to-one

  • This ensures f to the power of negative 1 end exponent open parentheses x close parentheses never gives out two or more outputs

    • which functions are not allowed to do

Worked Example

For the function space f left parenthesis x right parenthesis equals fraction numerator 2 x over denominator x minus 1 end fraction comma space x greater than 1:

(a) Find the inverse of space f left parenthesis x right parenthesis.

2-3-2-ib-aa-sl-inverse-functions-a-we-solution

(b) Find the domain of space f to the power of negative 1 end exponent left parenthesis x right parenthesis.

2-3-2-ib-aa-sl-inverse-functions-b-we-solution

(c) Find the value of k such that f left parenthesis k right parenthesis equals 6.

2-3-2-ib-aa-sl-inverse-functions-c-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Composite FunctionsNext:Graphing Functions & Their Key Features
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Mark Curtis

    Reviewer: Mark Curtis

    Expertise: Maths Content Creator

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.