Quadratic Functions & Graphs (DP IB Applications & Interpretation (AI)): Revision Note

Quadratic functions & graphs

What does a quadratic graph look like?

• A quadratic graph is of the form where .

• The value of affects the shape of the curve

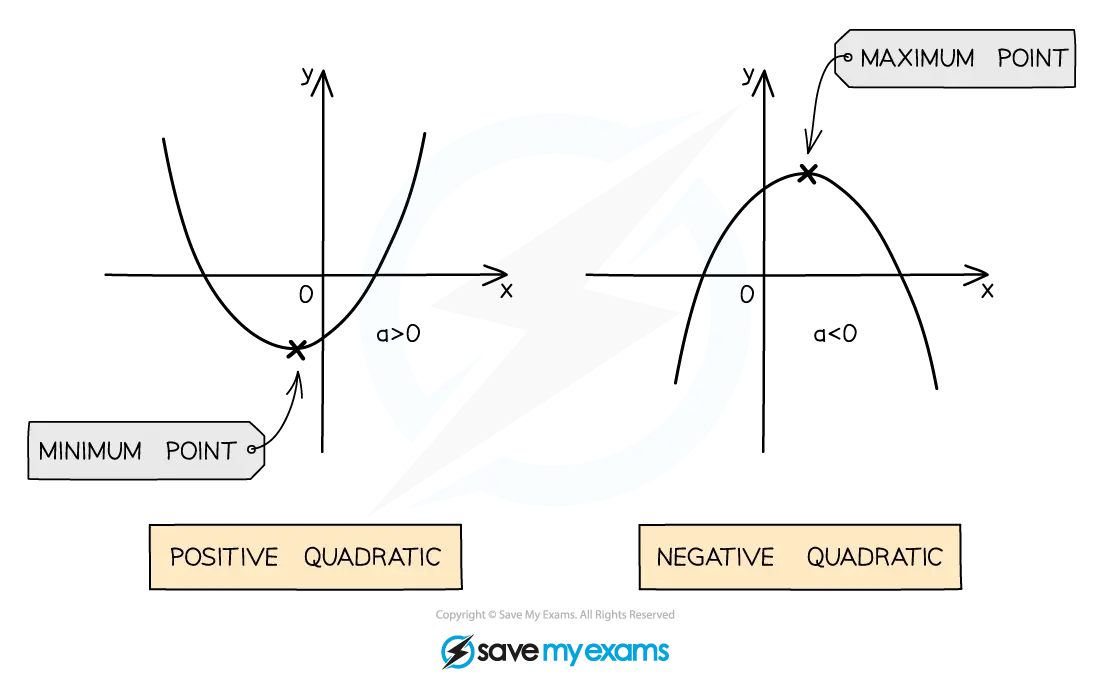
  • If is positive the shape is  and it has a minimum point

  • If is negative the shape is  and it has a maximum point

What are the key features of a quadratic graph?

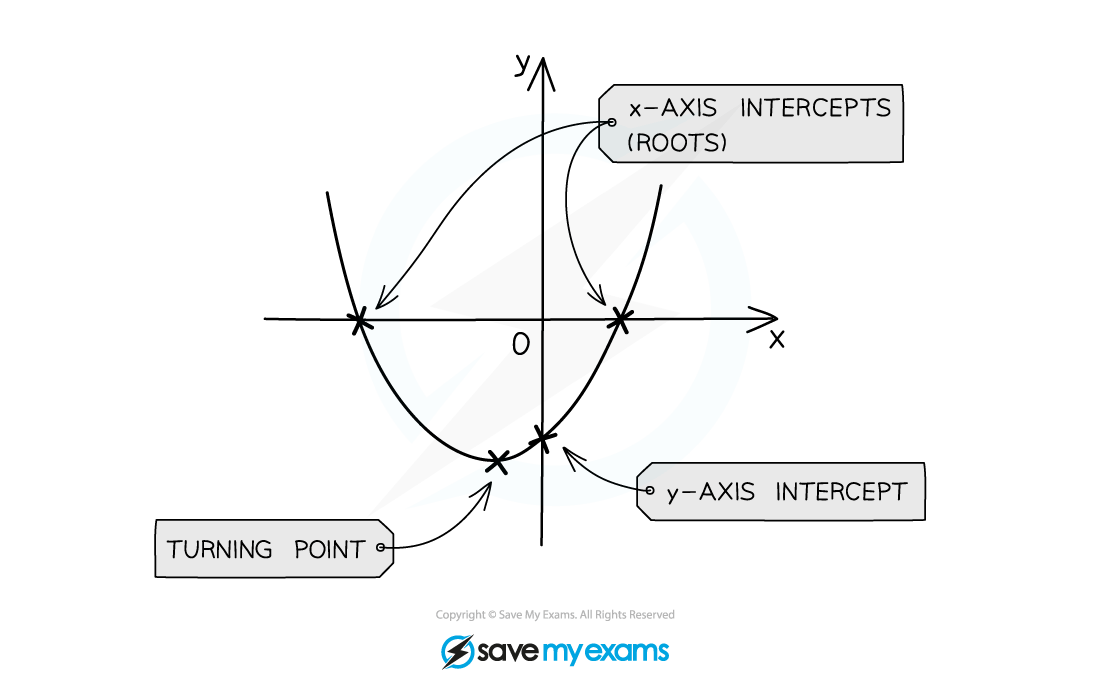
• The y-intercept is at the point

• The zeros or roots are the solutions to 

  • These can be found using your GDC or the quadratic formula

  • These are also called the x-intercepts

  • There can be 0, 1 or 2 x-intercepts

• There is an axis of symmetry at 

  • This is given in your formula booklet

  • If there are two x-intercepts then the axis of symmetry goes through the midpoint of them

• The vertex lies on the axis of symmetry

  • The x-coordinate is 

  • The y-coordinate can be found using the GDC or by calculating y when 

How do I sketch a quadratic graph?

• Determine its shape by looking at the value of

  • e.g. looks like

• Find the axis of symmetry using the formula

  • e.g.

• Find the vertex by substituting the x-coordinate into the equation

  • e.g.

  • vertex is at

• Find the roots using your GDC

  • e.g.

  • roots are and

• Label the y-intercept

  • e.g.

• Draw the graph going through all the labelled points