Introduction to Graph Theory (DP IB Applications & Interpretation (AI)): Revision Note

Graph Theory

What is a graph?

• A graph is a mathematical structure that is used to represent objects and the connections between them

  • They can be used in modelling many real-life applications

    • e.g. electrical circuits, flight paths, maps etc.

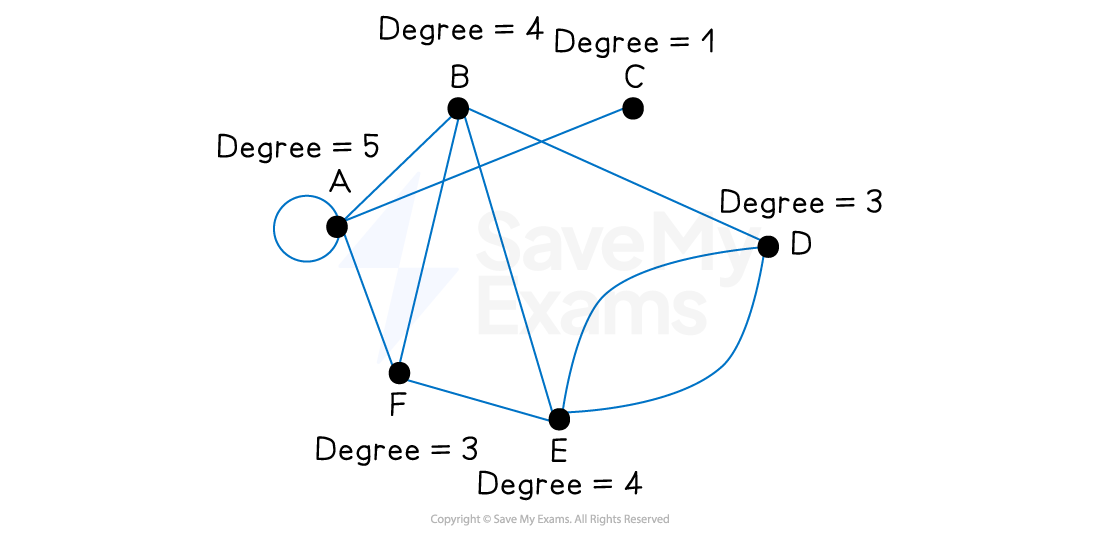
• A vertex (point) represents an object or a place

  • Vertices are labelled with letters or names

    • e.g. A, B, C, ... or England, Spain, France, ...

• An edge (line) forms a connection between two vertices

  • Adjacent edges share a common vertex

  • An edge that starts and ends at the same vertex is called a loop

  • There may be multiple edges connecting two vertices

• The degree of a vertex is the number of edges that are immediately connected to it

  • A loop counts as two edges when calculating the degree

  • An odd vertex has an odd degree and even vertex has an even degree

• Two vertices are adjacent if there is an edge between them

  • It is possible for a vertex to be adjacent to every other vertex

  • It is also possible for a vertex to not be adjacent to any other vertex

• Two edges are adjacent if they share a common vertex

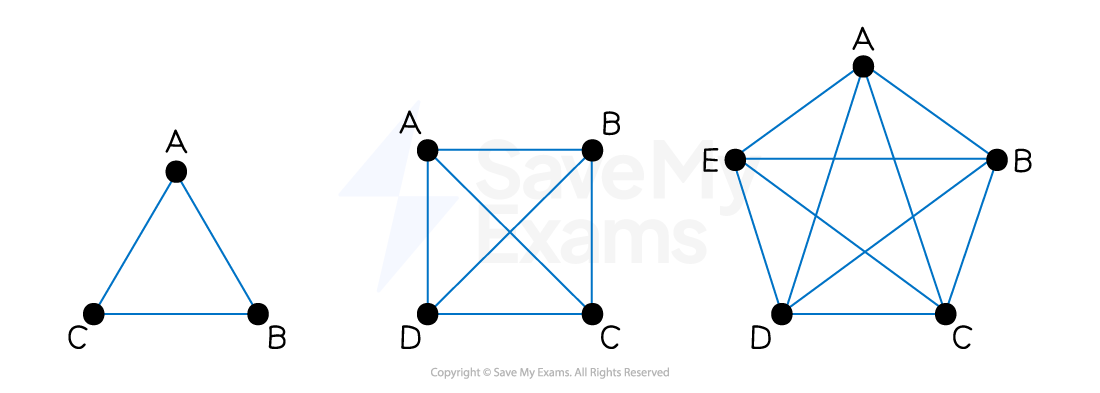
What is a complete graph?

• A complete graph is a graph in which each vertex is adjacent to every other vertex

  • There is exactly one edge between each pair of vertices

What is a simple graph?

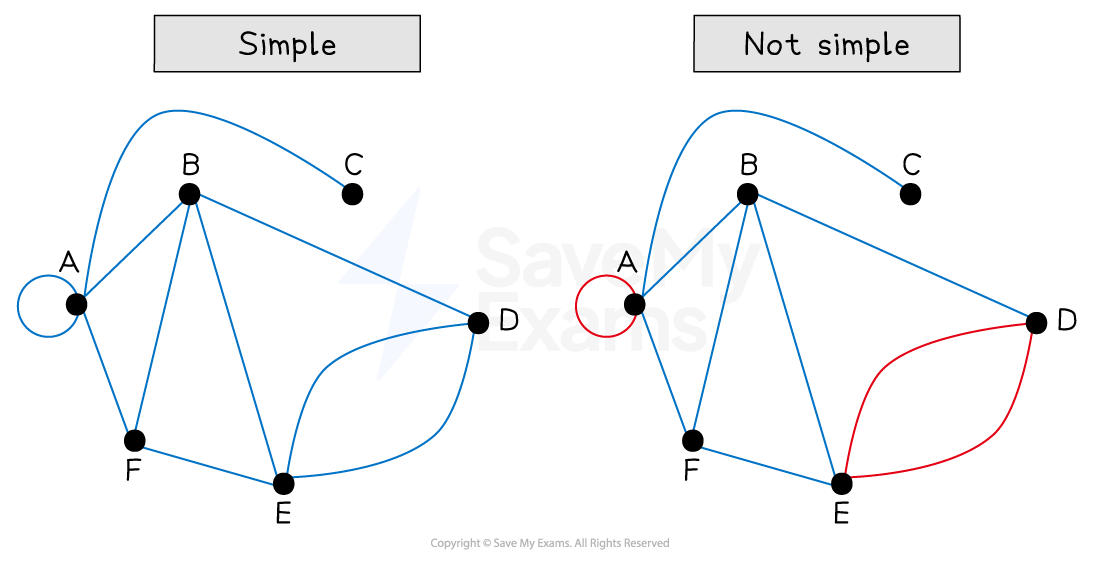
• A simple graph contains no loops or multiple edges

What is a weighted graph?

• The edges in a weighted graph are assigned numerical values such as distance or money

• For a simple graph

  • The sum of the weights of the edges is known as the weight of the graph

What are walks, trails, paths, circuits and cycles?

• A walk is a route through the graph using the edges

  • It is a sequence of vertices

  • Each vertex in the sequence is adjacent to the previous one

    • e.g. ABDBDBAAC is a walk

• A walk can be open or closed

  • It is open if the last vertex is different to the first vertex

  • It is closed if the last vertex is the same as the first vertex

• Trails, paths, circuits and cycles are types of walks

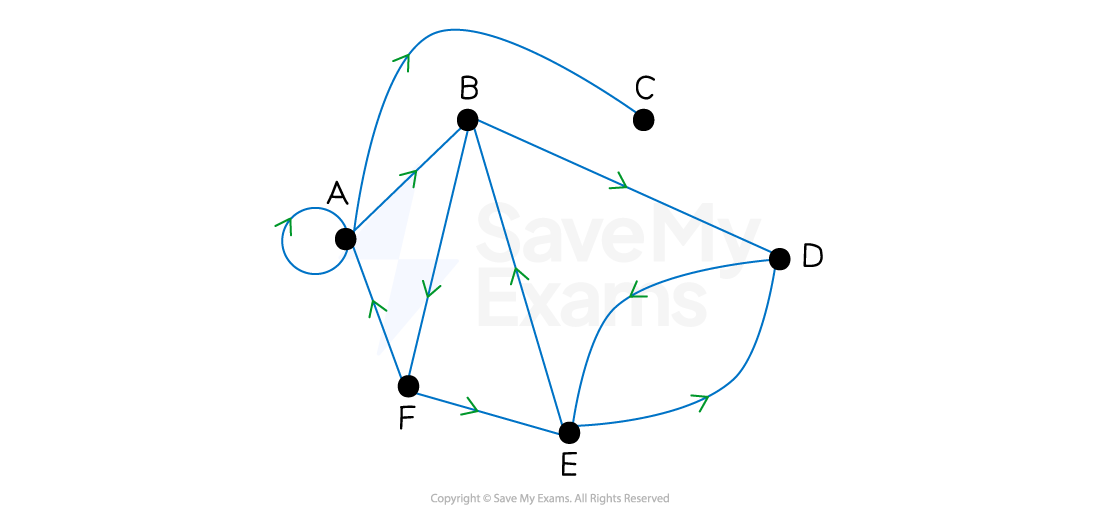
What is a directed graph?

• The edges in a directed graph can only be travelled along in the direction indicated

  • the in-degree of a vertex is the number of edges that lead to that vertex

  • the out-degree is the number of edges that leave from that vertex

• Each edge needs a direction

• If an edge between a pair of vertices can be traversed in either direction then

  • then there should be a repeated edge

  • each one goes in opposite directions

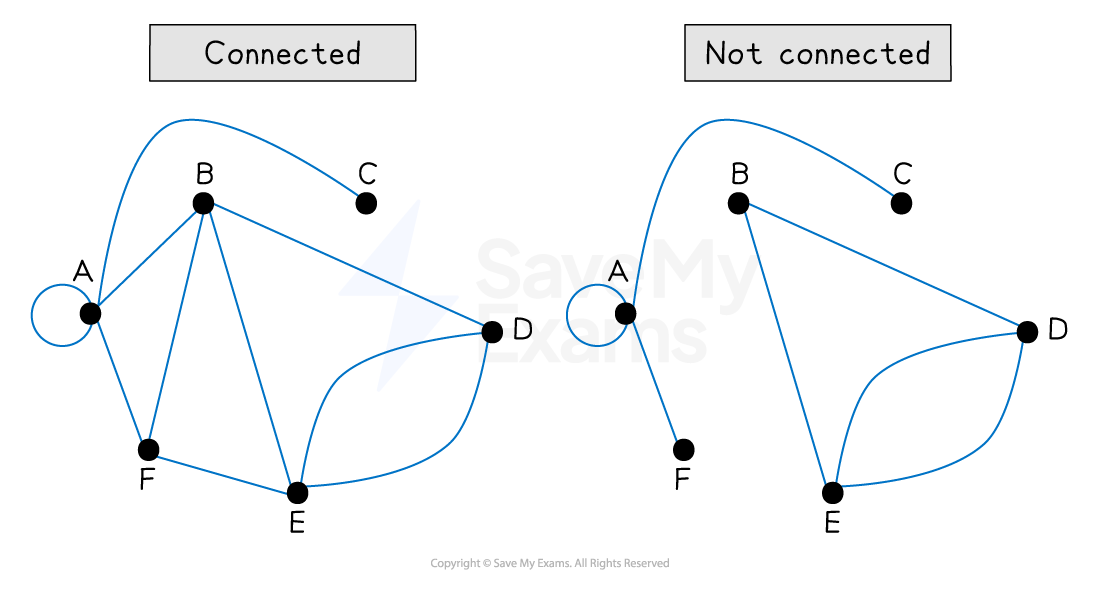
What is a connected graph?

• An undirected graph is connected if there is a path between any pair of vertices

  • This means you can get from any vertex to any other vertex

    • There does not need to be an edge between each pair of vertices

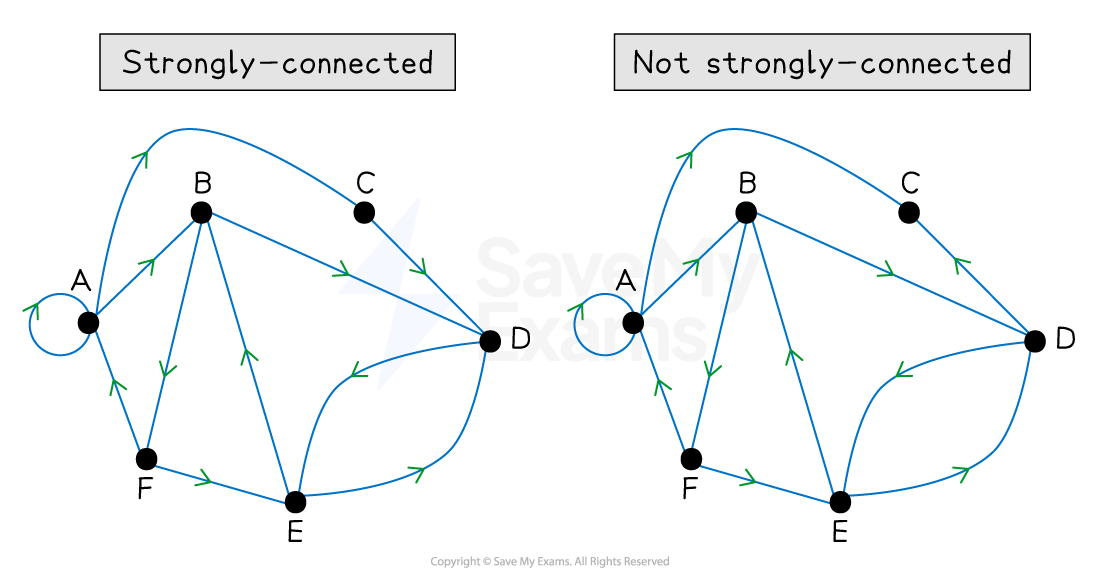
• A directed graph is strongly-connected if there is a path from any vertex to any other vertex

  • This means you can get from any vertex to any other vertex and back again

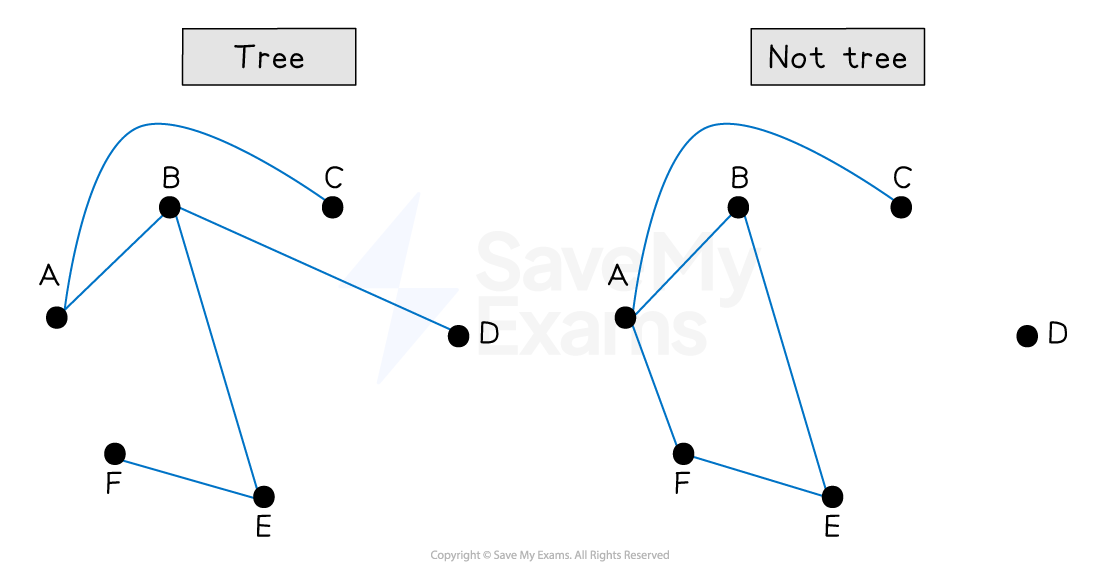
What is a tree?

• A tree is connected and does not contain cycles

  • A tree with n vertices has n - 1 edges

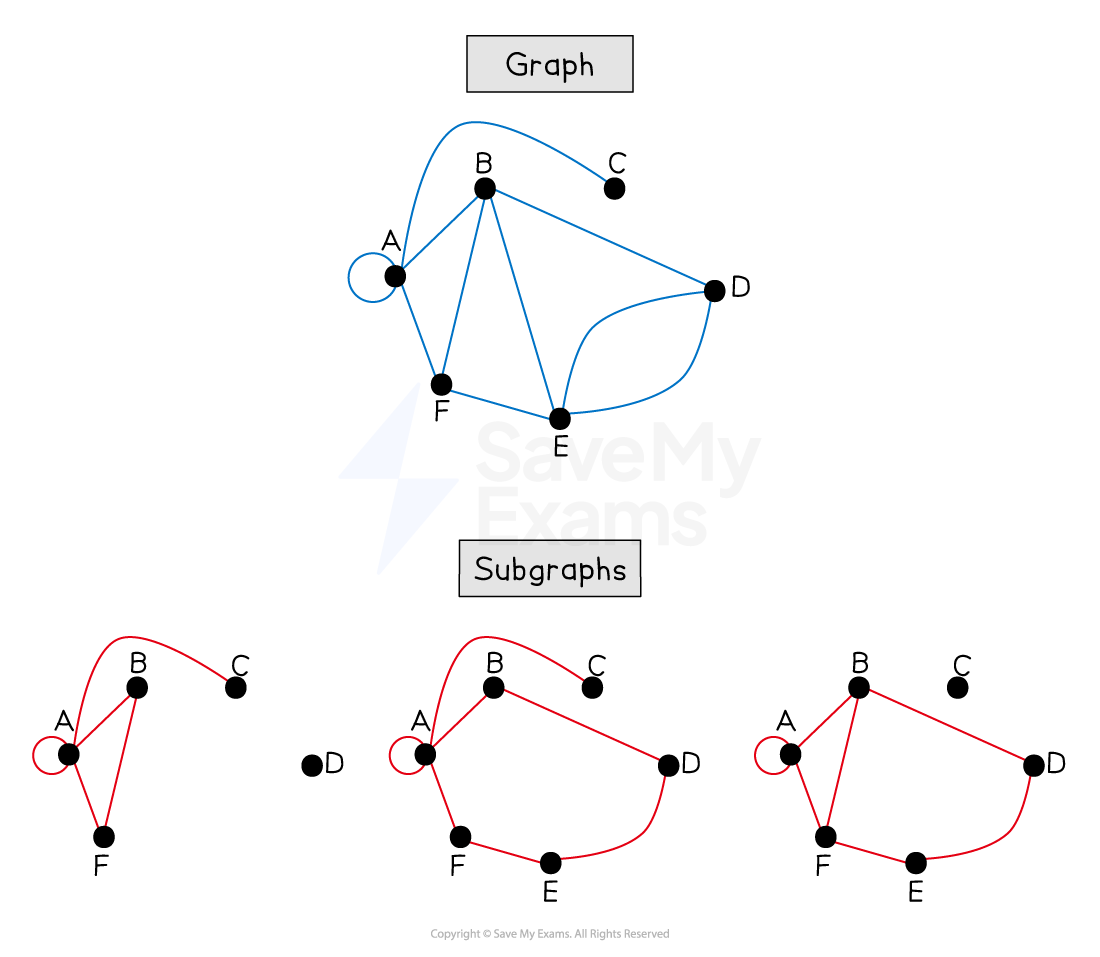
What is a subgraph?

• A subgraph of a graph only contain edges and vertices that appear in the graph

  • A subgraph is a graph itself

• A spanning tree is a subgraph that:

  • is a tree

  • includes all the vertices of the original graph