Graphing in Physics (DP IB Physics): Revision Note

Constructing graphs

Sketch graphs

• Sketch graphs are a way to describe the qualitative trend between variables

• Axes must be labelled, but they do not need to include scales or data points

• The shape of the graph depends on the relationship between the variables, such as

  • linear

  • non-linear

  • directly proportional

  • inversely proportional

Sketch graphs of Boyle's law

• For the graphs of pressure and volume above:

  • against is a linear (straight line) graph through the origin, indicating is proportional to

  • against is a non-linear (curved) graph, indicating is inversely proportional to

  • against is a straight, horizontal line, indicating is constant as increases

Linear graphs

• A straight line graph represents a linear relationship

  • This indicates the rate of change between two variables is constant

• If two variables, and , are directly proportional

  • the graph of against is a straight line passing through the origin

  • the calculated values of are constant

• All directly proportional graphs are linear, however, not all linear graphs are directly proportional

Non-linear graphs

• A curved graph represents a non-linear relationship

  • This indicates the rate of change between two variables is not constant

• If two variables, and , are inversely proportional:

  • the graph of against is a shallow curve which does not cross either axis

  • the graph of against is a straight line passing through the origin

  • the calculated values of are constant

Presenting and interpreting data

• Students are expected to be able to present and interpret raw and processed data in tables, charts, and graphs

  • Bar charts

    • Shows qualitative or discrete data as columns on a graph

    • Each column represents a qualitative variable

    • The height of the column indicates the size of the group

  • Pie charts

    • Shows proportions of qualitative or discrete data as slices on a circle

    • Each slice represents a qualitative variable

    • The size of each slice indicates the relative proportion of the variable

  • Histograms

    • Shows quantitative or continuous data as columns on a graph, but without spaces between adjacent columns

    • Each column represents a quantitative variable

    • The height of the column indicates the size of the group

  • Scatter graphs

    • Shows the correlation between continuous variables

    • Data points are plotted, and then a line of best fit is drawn

    • Example: A graph showing how the force applied to a spring affects its extension

  • Line/curve graphs

    • Shows functional relationships between variables

    • Data points are plotted and then connected in sequence by line

    • Example: A graph showing the distance travelled by a car over a certain period of time

Plotting graphs

• When plotting a graph, remember the following:

  • Label axes, and include units

    • The independent variable should go on the x-axis and the dependent variable should go on the y-axis

  • Use appropriate linear scales

    • Ensure that all data points are plotted within the graph area

    • The plotted points must occupy at least half or more of the sheet or grid

    • A rough rule of thumb is that if you can double the scale and still fit all the points on, then your scale is not appropriate

  • Plot data points accurately

    • The most common convention is to use small crosses to show the data points

Graph of distance versus time

• Remember: The independent variable is the one you control or manipulate and the dependent variable is the one that changes as a result of your manipulation

• Always draw data points in pencil as it makes it easier to make corrections and adjustments

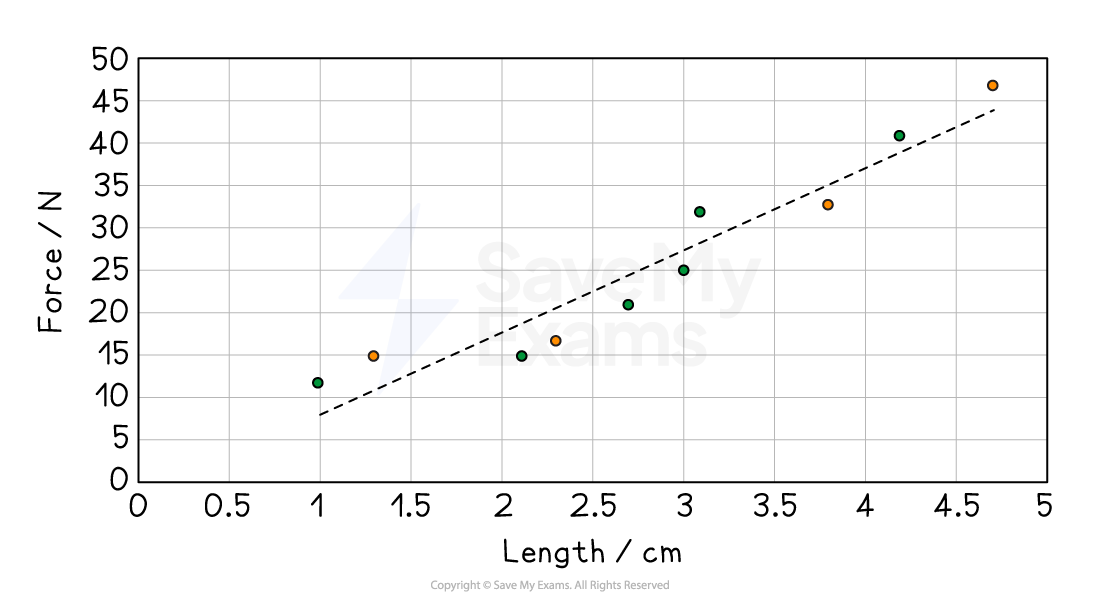
Lines of best fit

• Students often confuse the term lines of best fit with straight lines

• A line of best fit may be straight or curved, depending on the trend shown by the data

  • If the line of best fit is straight, make sure it is drawn with a ruler

  • If the line of best fit is a curve, make sure it is drawn smoothly

• A line of best fit should

  • have a balance of data points on either side of the line

  • be drawn through the origin (but only if the data and trend allow it)

How to draw a best-fit line

Interpreting graphs

Gradient

• On a linear (straight line) graph, the gradient is constant

• On a graph of against the gradient is equal to

• Where

  • = change in , or

  • = change in , or

• To find the gradient of a straight line

  • draw a large triangle

    • The triangle should be as large as possible to minimise precision errors

  • read off the values from the axes

    • When reading off values, you can utilise points that lie on the line of best fit, but not data points that lie away from the line

  • calculate the gradient using the above equation

    • The units of the gradient will be the ratio of the y variable unit and the x variable unit

    • e.g. for a graph of extension x (in m) against force F (in N) the units of the gradient would be N m^-1

Changes in gradient

• The gradient of a curved line is constantly changing

• To find the gradient of a point on a curve

  • Draw a tangent to the graph, using a ruler to line up against the curve at the point where the gradient is to be measured

  • Then, use the equation for a straight line to calculate the gradient

How to draw a tangent to a curve

Intercepts

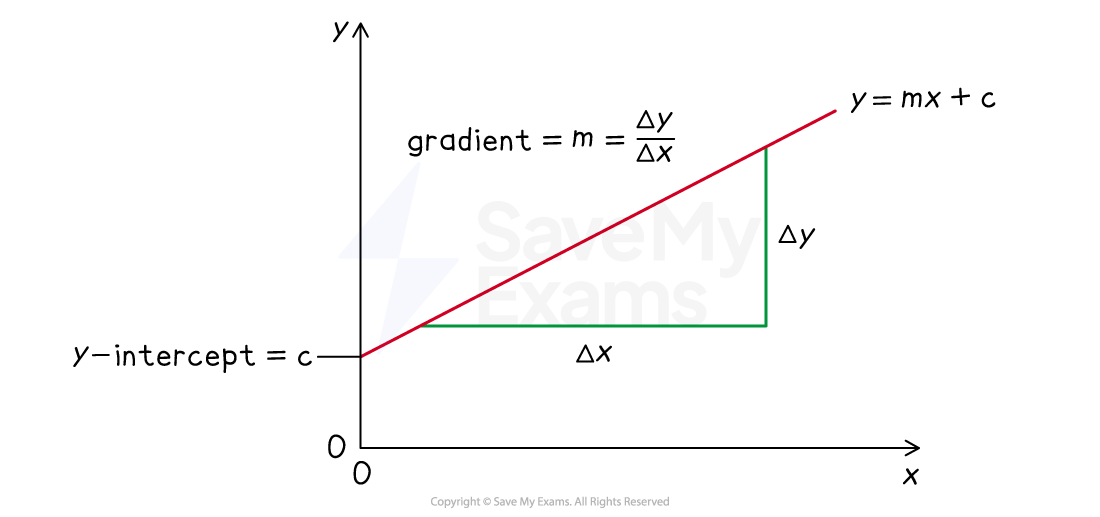
• The equation for a straight line is y = mx + c, where:

  • y = dependent variable

  • x = independent variable

  • m = slope

  • c = y-intercept

• The y-intercept is the y value obtained where the line crosses the y-axis when x = 0

Equation of a straight line

Maxima and minima

• The maxima and minima are the highest and lowest points respectively

  • Maxima - the gradient goes from positive to 0 to negative

  • Minima - the gradient goes from negative to 0 to positive

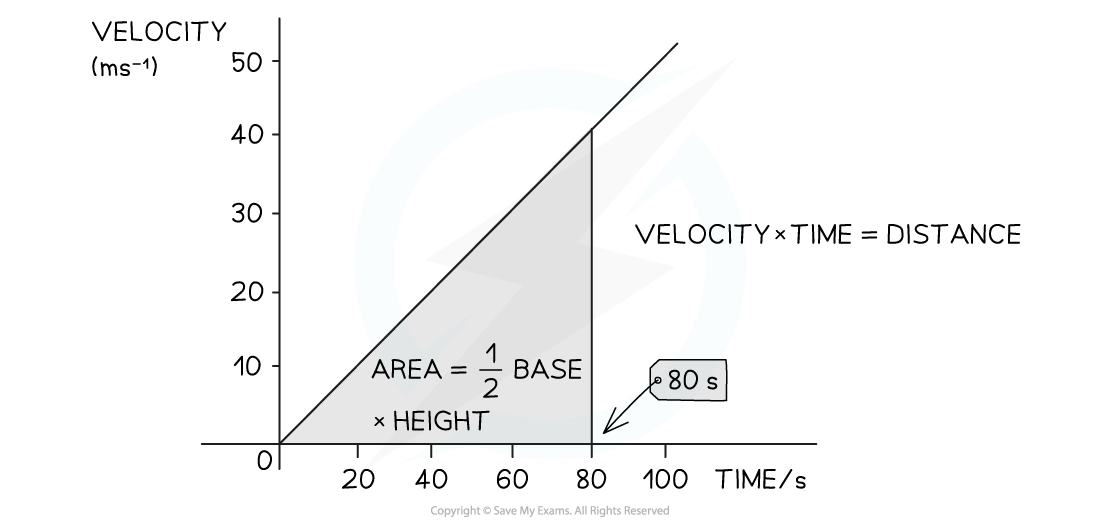
Areas under the graph

• The area under a graph often represents a physical quantity

  • e.g. the area under a velocity-time graph represents displacement

• When the area is a rectangle or a triangle, it is easy to find by calculating

area of rectangle = base × height

area of a triangle = ½ × base × height

How to find the area under a straight line

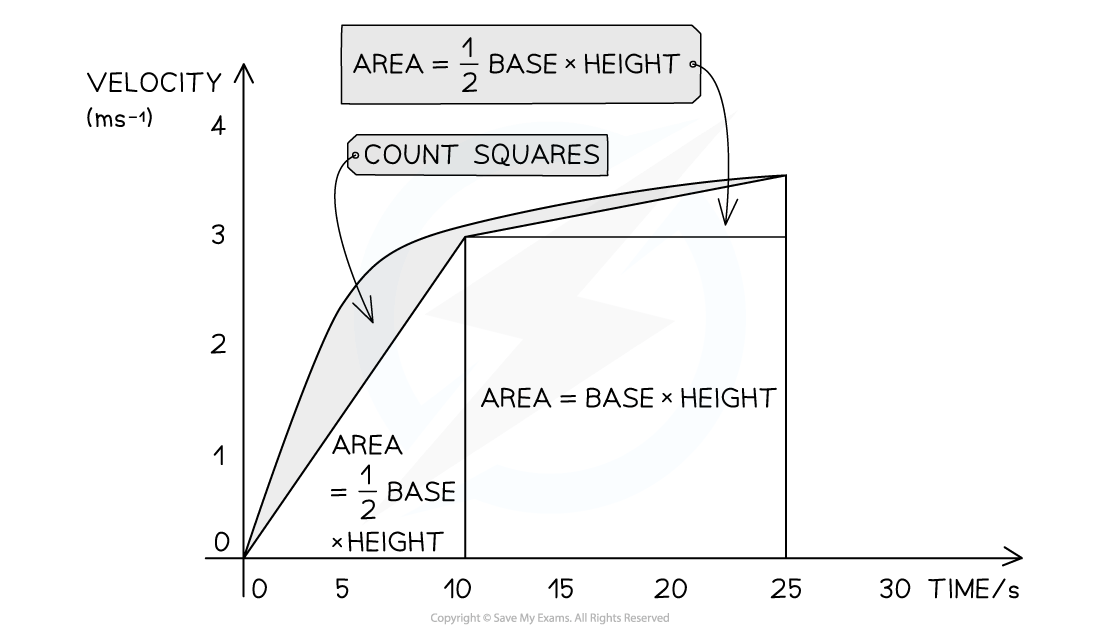
• When the line is curved, area is found though the following steps

  • Divide the shape into rectangles and triangles as shown

  • Find the area for each by calculating

  • Count the remaining squares

  • Add the totals together

How to find the area under a curved line

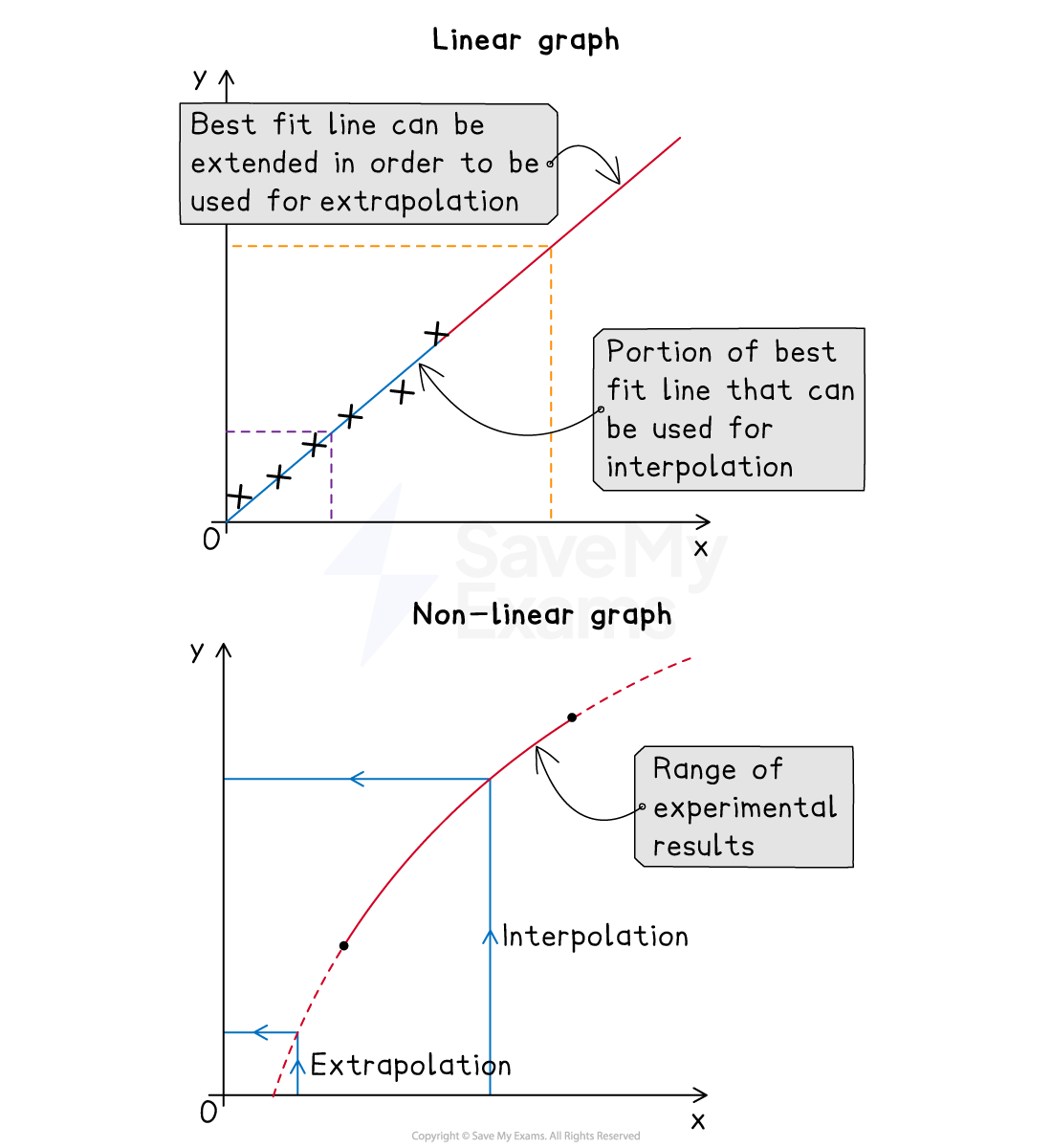
Extrapolating and interpolating graphs

• Extrapolation is extending a line of best fit to estimate values that lie beyond the data points of a graph

• Interpolation is using a line of best fit to estimate values that lie between data points of a graph

Extrapolation and interpolation on a graph

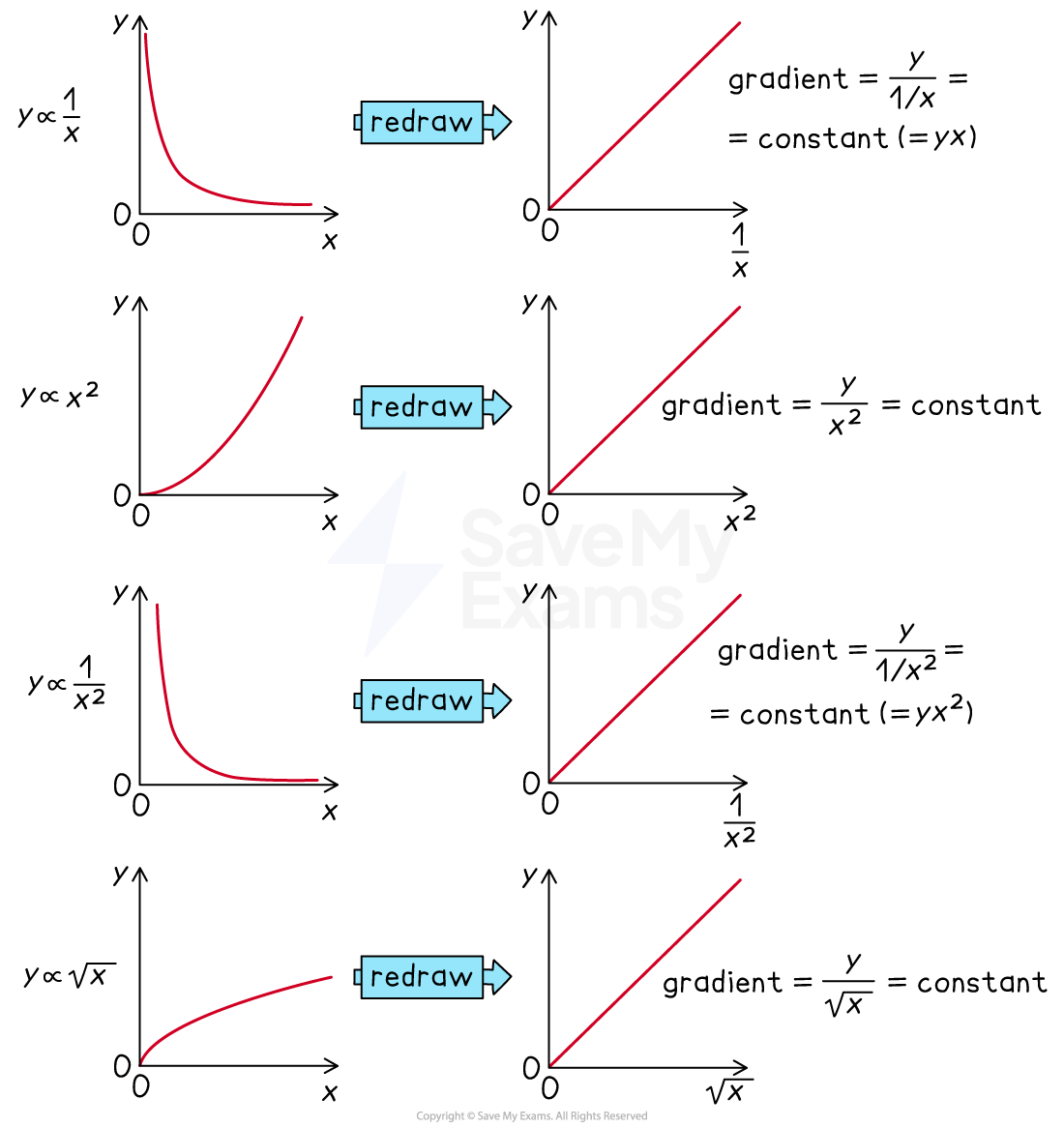
Linearising graphs

• Linear (straight line) graphs are easier to interpret than non-linear graphs

• Linearising a graph involves rearranging the variables in a non-linear relationship to fit the equation of a straight line y = mx + c

  • e.g. the time period of a pendulum is

  • Squaring both sides gives

  • Therefore, for a graph of against , gradient =

Common linearised relationships

Logarithmic graphs

What are logarithmic scales?

• Logarithmic scales are scales where intervals increase exponentially

  • A normal scale might go 1, 2, 3, 4, ...

  • A logarithmic scale might go 10¹, 10², 10³, 10⁴, ...

• Sometimes we can keep the scales with constant intervals by changing the variables

  • If the values of x increase exponentially: 10¹, 10², 10³, 10⁴, ...

  • Then you can use the variable log x instead which will have the scale: 1, 2, 3, 4, ...

  • This will change the shape of the graph

  • If the graph transforms into a straight line, then it is easier to analyse

• The numbers in a logarithmic scale represent logarithms, or powers, of a base number (usually 10 or e)

Why do we use logarithmic scales?

• Logarithmic scales are useful when analysing quantities which vary over several orders of magnitude

• When variables have a large range, it can be difficult to plot them on one graph

  • Especially when a lot of the values are clustered in one region

• If we are interested in the rate of growth or decay of a variable, rather than the actual values, then a logarithmic scale is useful

Constructing logarithmic graphs

Semi-log graphs

• A semi-log graph is used when only one scale (the y-axis) of the original graph is logarithmic

• Graphs of exponential functions appear as straight lines on semi-log graphs

• If

  • Takes logs of both sides

    • 

  • Split the right-hand side into two terms

    • 

  • Bring down the power

    • 

• This is of the form , where

  • is on the -axis and is on the -axis

  • the gradient is and the y-intercept is

Log-log graphs

• A log-log graph is used when both scales of the original graph are logarithmic

• Graphs of power functions appear as straight lines on log-log graphs

• If

  • Takes logs of both sides

    • 

  • Split the right-hand side into two terms

    • 

  • Bring down the power

    • 

• This is of the form , where

  • is on the -axis and is on the -axis

  • the gradient is and the y-intercept is

• For example, consider Kepler's law:

• The relationship between T and r can be shown using a log-log graph

• The graph of log T in years against log r in AU (astronomical units) for the planets in our solar system is a straight-line graph

Kepler's law as a log-log graph

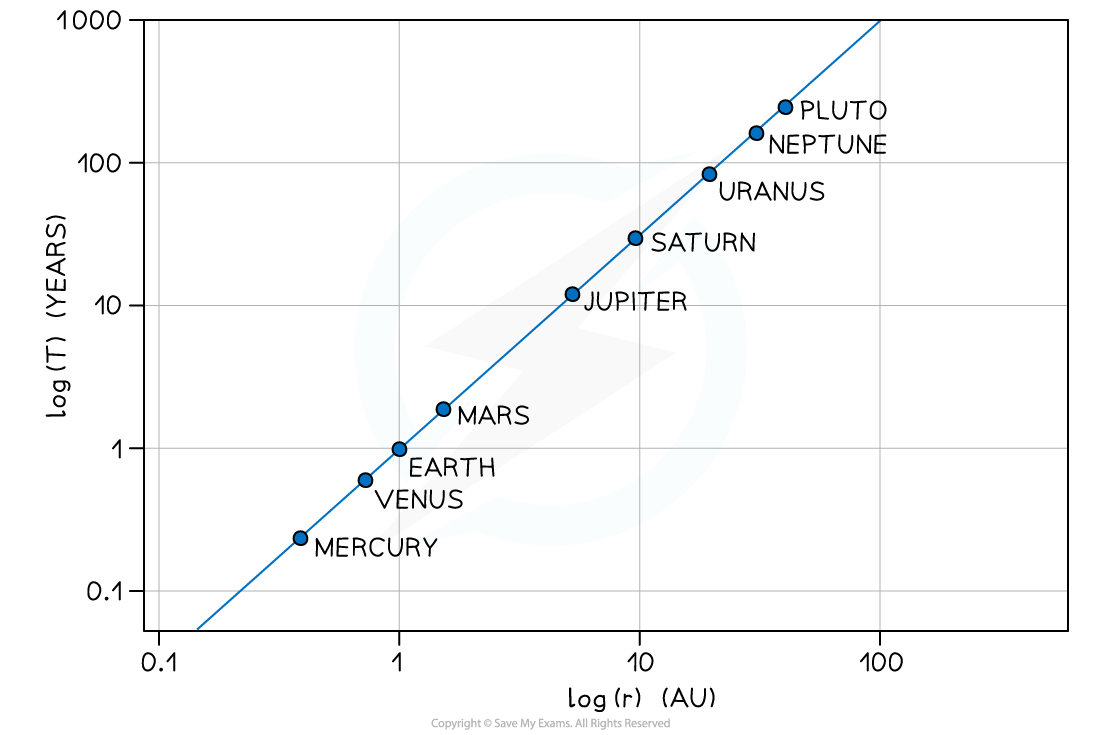
The logarithmic graph of log T against log r gives a straight line

• The graph does not go through the origin since it has a negative y-intercept

  • Only the graph of log T and log r will produce a straight-line graph, a graph of T vs r would not