Introduction to Differentiation (Cambridge (CIE) O Level Additional Maths): Revision Note

Exam code: 4037

Author

Amber

Last updated

27 June 2025

Did this video help you?

Definition of gradient

What is the gradient of a curve?

At a given point the gradient of a curve is defined as the gradient of the tangent to the curve at that point
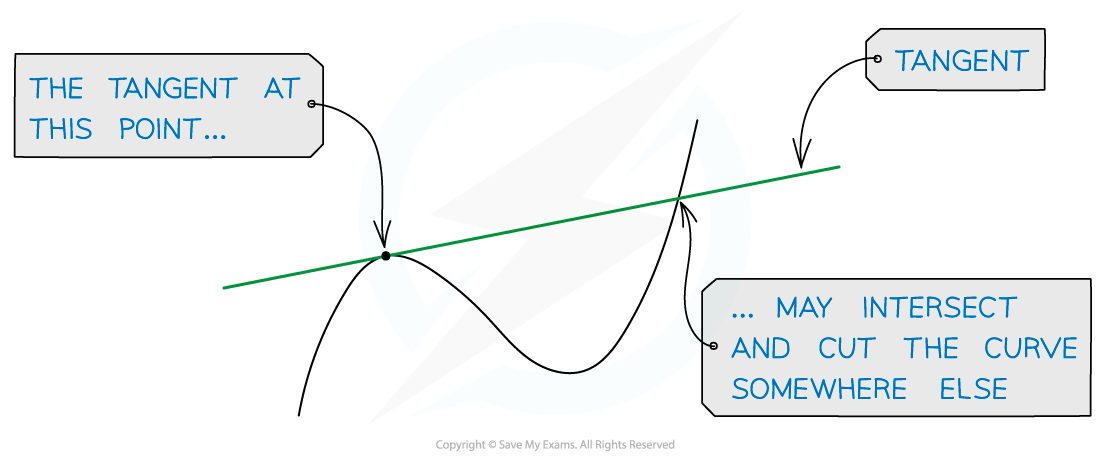
A tangent to a curve is a line that just touches the curve at one point but doesn't cut the curve at that point

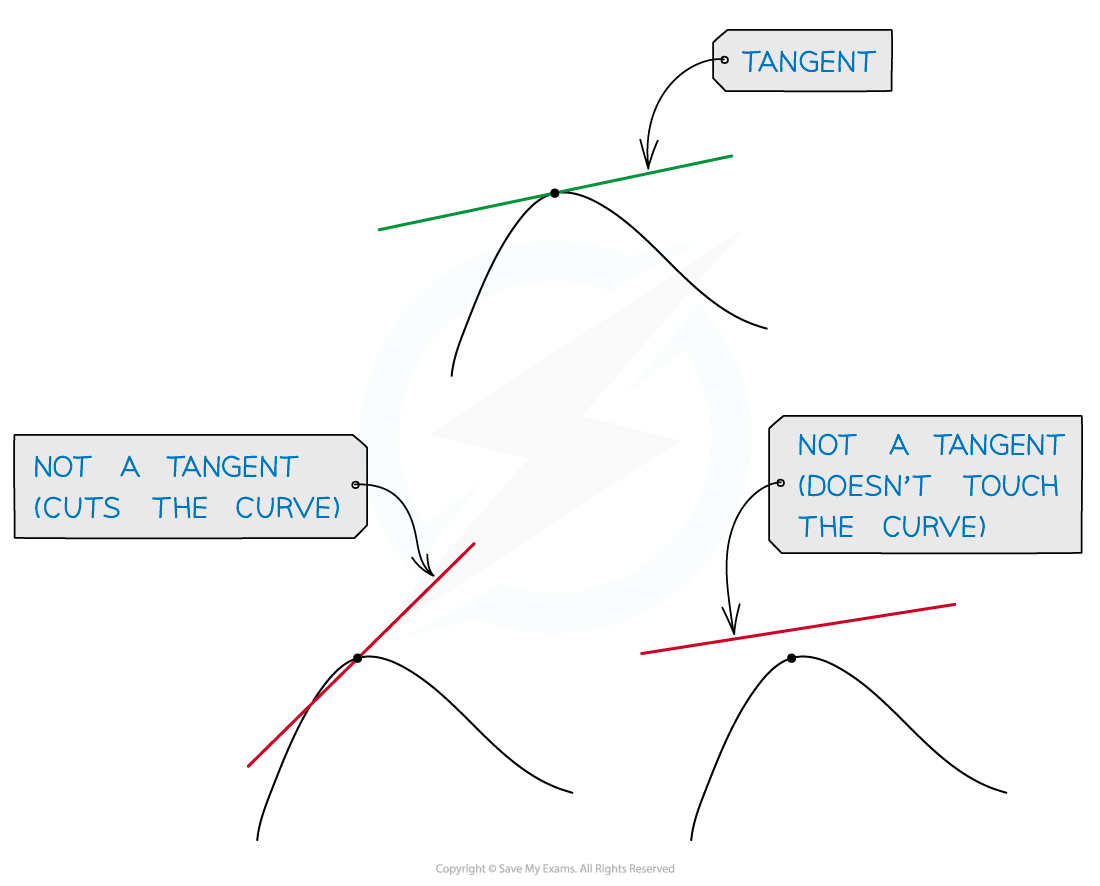
Def Grad Illustr 1, A Level & AS Maths: Pure revision notes

A tangent may cut the curve somewhere else on the curve

Def Grad Illustr 2, A Level & AS Maths: Pure revision notes

It is only possible to draw one tangent to a curve at any given point
Note that unlike the gradient of a straight line, the gradient of a curve is constantly changing

Examiner Tips and Tricks

If a question asks for the "rate of change of ..." then it is asking for the "gradient"

Worked Example

The diagram shows the curve with equation $y = x^{3} - 2 x^{2} - x + 3 .$ The tangent, $T$ , to the curve at the point $A (2, 1)$ is also shown.

Using the diagram, calculate the gradient of the curve at $A$ .

The gradient of the curve at the point A is the same as the gradient of the tangent T. Calculate the gradient of the line.

$\frac{4 - (- 2)}{3 - 1}$

The gradient is 3

Definition of derivatives

What is a derivative?

Calculus is about rates of change
- the way a car’s position on a road changes is its speed (velocity)
- the way the car’s speed changes is its acceleration
The gradient (rate of change) of a (non-linear) function varies with $x$
The derivative of a function is a function that relates the gradient to the value of $x$
- For example, the derivative of $y = x^{2}$ is $2 x$
  - This means that when $x = 1$ , the gradient of $y = x^{2}$ is $2 (1) = 2$
  - And when $x = 5$ , the gradient of $y = x^{2}$ is $2 (5) = 10$
The derivative is also called the gradient function

Worked Example

The derivative of $y = x^{3} - 2 x^{2} - x + 3$ is $3 x^{2} - 4 x - 1$ .

Use the derivative to find the gradient of $y = x^{3} - 2 x^{2} - x + 3$ at the point $A (2, 1)$ .

Substitute $x = 2$ into the derivative, $3 x^{2} - 4 x - 1$

$3 {(2)}^{2} - 4 (2) - 1 = 12 - 8 - 1$

gradient = 3

Note that the answer is the same as in the method above

Did this video help you?

Differentiating powers of x

What is differentiation?

Differentiation is the process of finding an expression for the derivative (gradient function) from the equation of a curve
- The equation of the curve is written $y = . . .$ and the gradient function is written $\frac{d y}{d x} = . . .$

How do I differentiate powers of x?

Powers of $x$ are differentiated according to the following formula:
- If $y = a x^{n}$ then $\frac{d y}{d x} = a n x^{n - 1}$
  - e.g. If $y = 4 x^{3}$ then $\frac{d y}{d x} = 4 \times 3 \times x^{3 - 1} = 12 x^{2}$
  - you "bring down the power" then "subtract one from the power"
Don't forget these two special cases:
- If $y = a x$ then $\frac{d y}{d x} = a$
  - e.g. If $y = 6 x$ then $\frac{d y}{d x} = 6$
- If $y = a$ then $\frac{d y}{d x} = 0$
  - e.g. If $y = 5$ then $\frac{d y}{d x} = 0$
- These allow you to differentiate linear terms in $x$ and constants
Functions involving fractions with denominators in terms of $x$ will need to be rewritten as negative powers of $x$ first
- e.g. If $y = \frac{4}{x}$ then rewrite as $y = 4 x^{- 1}$ and differentiate

How do I differentiate sums and differences of powers of x?

The formulae for differentiating powers of $x$ work for a sum or difference of powers of $x$
- e.g. If $y = 5 x^{4} + 3 x^{- 2} + 4$ then $\frac{d y}{d x} = 5 \times 4 x^{4 - 1} + 3 \times (- 2) x^{- 2 - 1} + 0$ $\frac{d y}{d x} = 20 x^{3} - 6 x^{- 3}$
- This is sometimes referred to differentiating 'term-by-term'
Products and quotients (divisions) cannot be differentiated in this way so they need expanding/simplifying first
- e.g. If $y = (2 x - 3) (x^{2} - 4)$ then expand to $y = 2 x^{3} - 3 x^{2} - 8 x + 12$ which is a sum/difference of powers of $x$ and can then be differentiated

What can I do with derivatives (gradient functions)?

The derivative can be used to find the gradient of a function at any point
- The gradient of a function at a point is equal to the gradient of the tangent to the curve at that point
- A question may refer to the gradient of the tangent

Examiner Tips and Tricks

Don't try to do too many steps in your head; write the expression in a format that you can differentiate before you actually differentiate it
- e.g. $y = \frac{1}{x^{4}} + \frac{2}{x^{3}}$ can be rewritten as $y = x^{- 4} + 2 x^{- 3}$ which is then far easier to differentiate

Worked Example

Find the derivative of

(a) $\begin{matrix} \end{matrix}$ $y = 5 x^{3} + 2 x + \frac{3}{x^{2}} + 8$

Rewrite the $\frac{3}{x^{2}}$ term

$y = 5 x^{3} + 2 x + 3 x^{- 2} + 8$

Apply the rule for differentiating powers ( $y = a x^{n}, \frac{d y}{d x} = a n x^{n - 1}$ ) and apply the special cases for the terms $2 x$ and 8 ( $y = a x, \frac{d y}{d x} = a$ and $y = a, \frac{d y}{d x} = 0$ )

$\frac{d y}{d x} = 15 x^{2} + 2 - 6 x^{- 3}$

Unless a question specifies there is not usually a need to rewrite/simplify the answer

$\frac{d y}{d x} = 15 x^{2} + 2 - \frac{6}{x^{3}}$

(b) $y = {(2 x + 3)}^{2}$

This is a product of two (equal) brackets so cannot be differentiated directly Expand the brackets to get an expression in powers of $x$ Take time to get the expansion correct, writing stages out in full if necessary

$\begin{array}{rcl} y & = & (2 x + 3) (2 x + 3) \\ y & = & 4 x^{2} + 6 x + 6 x + 9 \\ y & = & 4 x^{2} + 12 x + 9 \end{array}$

Differentiate 'term-by-term', looking out for those special cases

$\frac{d y}{d x} = 8 x + 12$

There is a factor of 4 but there is no demand to factorise the final answer in the question

$\frac{d y}{d x} = 8 x + 12$

This is a quotient so cannot be differentiated directly Spot the single denominator which means we can split the fraction by the two terms on the numerator

$y = \frac{8 x^{6}}{2 x^{4}} - \frac{x^{3}}{2 x^{4}}$

Simplify using the laws of indices

$y = 4 x^{6 - 4} - \frac{1}{2} x^{3 - 4} y = 4 x^{2} - \frac{1}{2} x^{- 1}$

Each term is now a power of $x$ , so differentiate 'term-by-term'

$\frac{d y}{d x} = 8 x + \frac{1}{2} x^{- 2}$

There is demand to simplify or write the answer in a particular form

$\frac{d y}{d x} = 8 x + \frac{1}{2} x^{- 2}$

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Compose & Resolve VelocitiesNext:Differentiating Special Functions

Introduction to Differentiation (Cambridge (CIE) O Level Additional Maths): Revision Note

Definition of gradient

What is the gradient of a curve?

Definition of derivatives

What is a derivative?

Differentiating powers of x

What is differentiation?

How do I differentiate powers of x?

How do I differentiate sums and differences of powers of x?

What can I do with derivatives (gradient functions)?

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Algebra & Functions

Functions

Language of Functions

Inverse Functions

Composite Functions

Quadratic Functions

Solving Quadratics by Factorising

Quadratic Formula

Completing the Square

Quadratic Equation Methods

Discriminants

Quadratic Graphs

Quadratic Inequalities

Factors of Polynomials

Operations with Polynomials

Polynomial Division

Factor & Remainder Theorem

Solving Cubic Equations

Equations, Inequalities & Graphs

Modulus Functions

Graphs of Cubic Polynomials

Simultaneous Equations

Linear Simultaneous Equations

Quadratic Simultaneous Equations

Logarithmic & Exponential Functions

Exponential Functions

Logarithmic Functions

Laws of Logarithms

Exponential Equations

Transforming Relationships to Linear Form

Coordinate Geometry

Straight-Line Graphs

Linear Graphs

Parallel & Perpendicular Lines

Coordinate Geometry of the Circle

Equation of a Circle

Tangents to Circles

Intersection of Two Circles

Trigonometry

Circular Measure

Radian Measure

Arcs & Sectors

Trigonometry

Trigonometric Functions

The Unit Circle

Graphs of Trigonometric Functions

Trigonometric Identities

Solving Trigonometric Equations

Trigonometric Proof

Sequences & Series

Permutations & Combinations

Permutations

Combinations

Problem Solving with Permutations & Combinations

Binomial Theorem

Binomial Theorem

Arithmetic & Geometric Progressions

Language of Sequences & Series

Arithmetic Progressions

Geometric Progressions

Vectors

Vectors in Two Dimensions

Introduction to Vectors

Vector Addition

Problem Solving using Vectors

Compose & Resolve Velocities

Calculus

Differentiation