Vector Addition (Cambridge (CIE) O Level Additional Maths): Revision Note

Vector addition

What is vector addition?

• Adding vectors together lets us describes the movement between two points

• To add or subtract vectors numerically simply add or subtract each of the corresponding components

• In column vector notation just add the top, middle and bottom parts together

  • For example: 

• In base vector notation add each of the i and j components together separately

  • For example: (2i + j) – (i + 4j) = (i – 3j)  

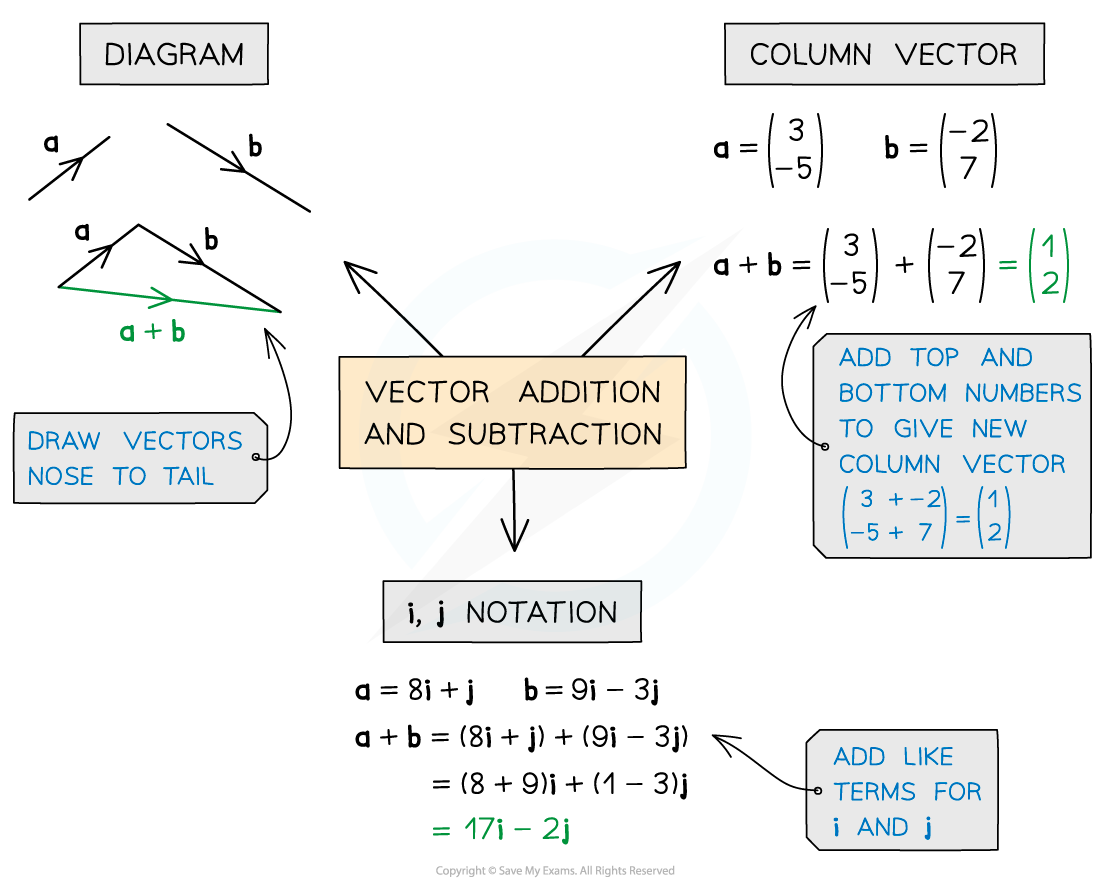
• Adding vectors creates a single vector which is called the resultant vector

  • The resultant vector will be the shortest route from the start of the first vector to the end of the second

• Subtracting a vector is the same as adding a negative vector

• Adding the vectors PQ and QP gives the zero vector, denoted by a bold zero 0 (0 in handwriting)

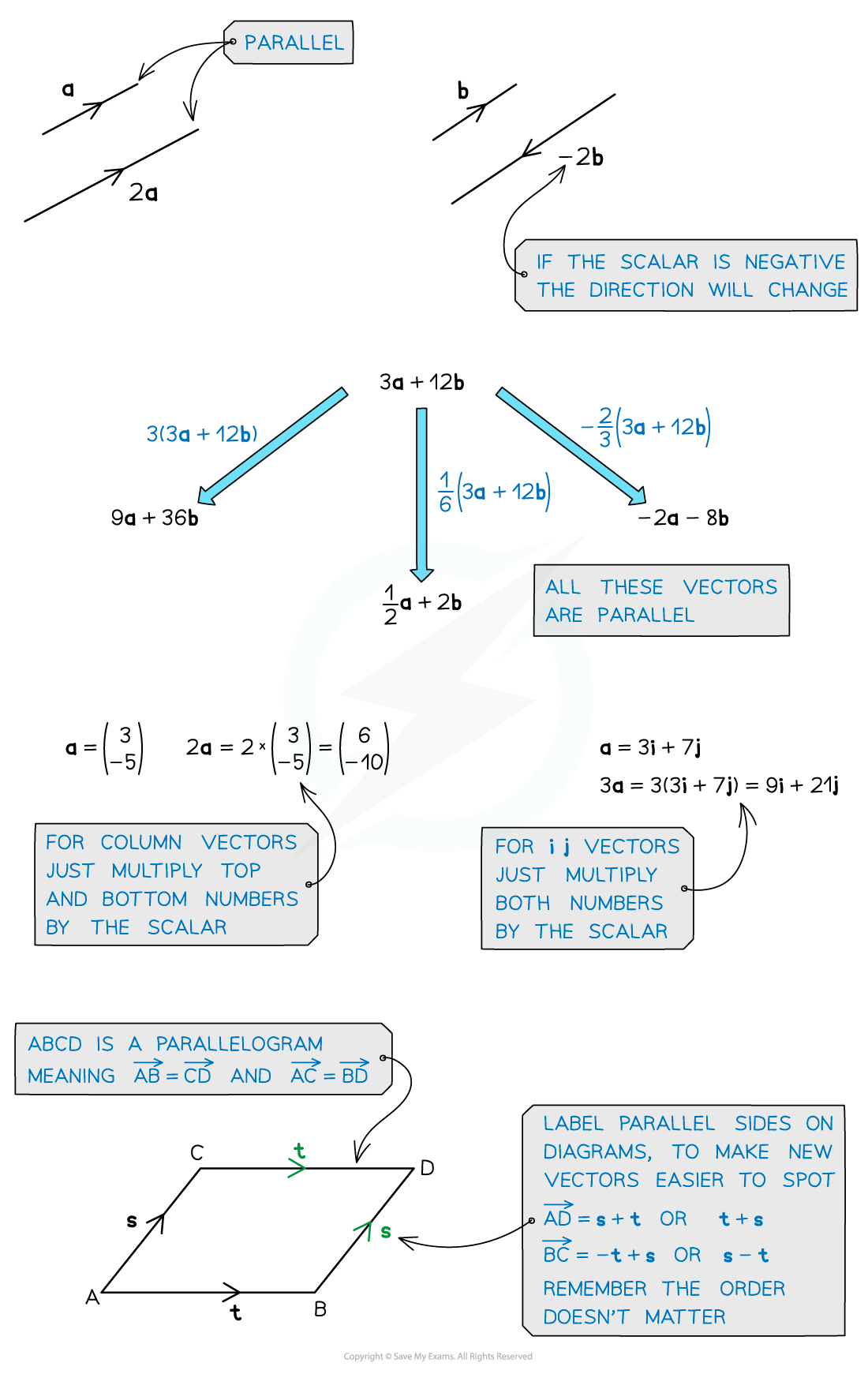
What are scalars and parallel vectors?

• Two vectors are parallel if and only if one is a scalar multiple of the other

  • i.e both components of the vector have been multiplied by the same constant 

• Multiplying a vector by a positive scalar changes the magnitude (size) but not its direction

• Multiplying a vector by a negative scalar changes the magnitude and the direction would be reversed 

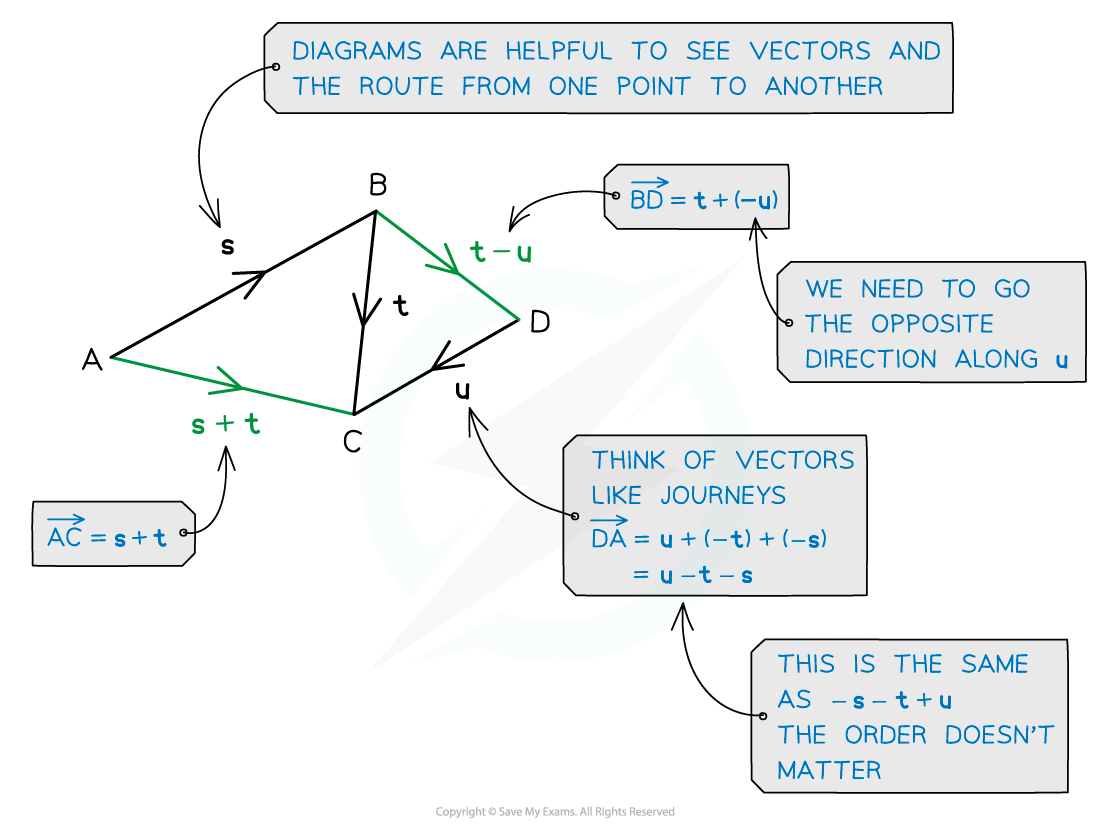
How do I find the vector between two points?

• If, relative to the origin , the points  and  have position vectors

  • 

  • 

then

• 

• Similarly, 

• This result is particularly useful when working with position vectors (as the 'journey' can always go via the origin)

  • but the result applies to any set of three vectors