Completing the Square (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Completing the square
Why is completing the square for quadratics useful?
Completing the square gives the maximum or minimum of a quadratic function
This can be used to define the range of the function
It gives the vertex when drawing the graph
It can be used to solve quadratic equations
It can be used to derive the quadratic formula
How do I complete the square for a monic quadratic of the form x2+bx+c?
Halve the value of
and write down
This is because
so it is similar to
Subtract the unwanted
term and add on the constant
For example,
How do I complete the square for a non-monic quadratic of the form ax2+bx+c?
Factorise out the
from the terms involving
Leaving the
un-factorised will avoid working with lots of fractions
Complete the square on the quadratic term inside the bracket
Halve
and write
This is because
Subtract the unwanted
term
Multiply through by
and add on
For example,
Examiner Tips and Tricks
Some questions may not use the phrase "completing the square" so ensure you can recognise a quadratic expression or equation written in the form
How do I use completing the square to optimise with quadratics?
You can use the completed square form to find the maximum or minimum of an expression
The optimal value of
is
It is a maximum if
is positive
It is a minimum if
is negative
The optimal value occurs when
For example, suppose
is the profit in dollars when
units are sold
The maximum profit is $3000
This is achieved when 50 units are sold
Worked Example
Complete the square on the following expressions.
(i) .
Answer:
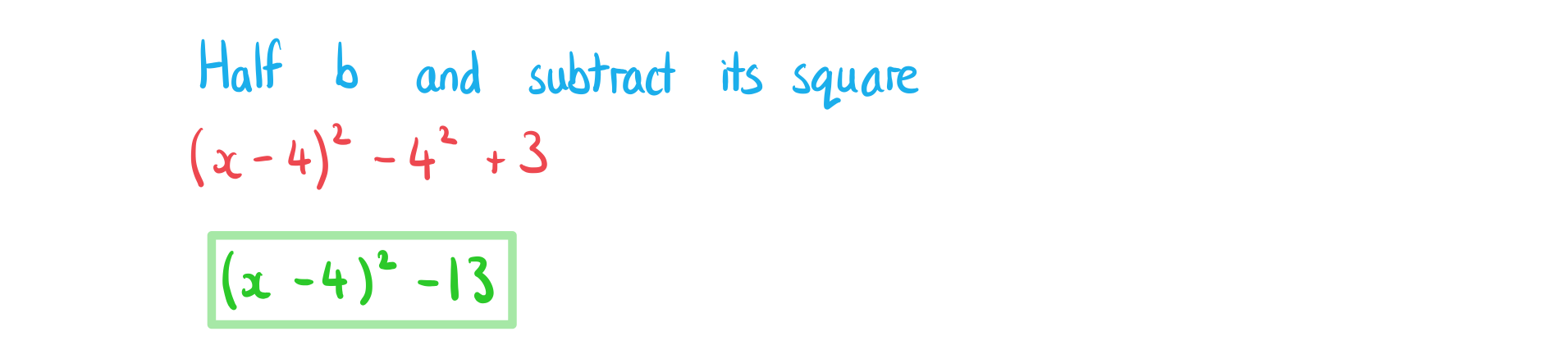
(ii) .
Answer:
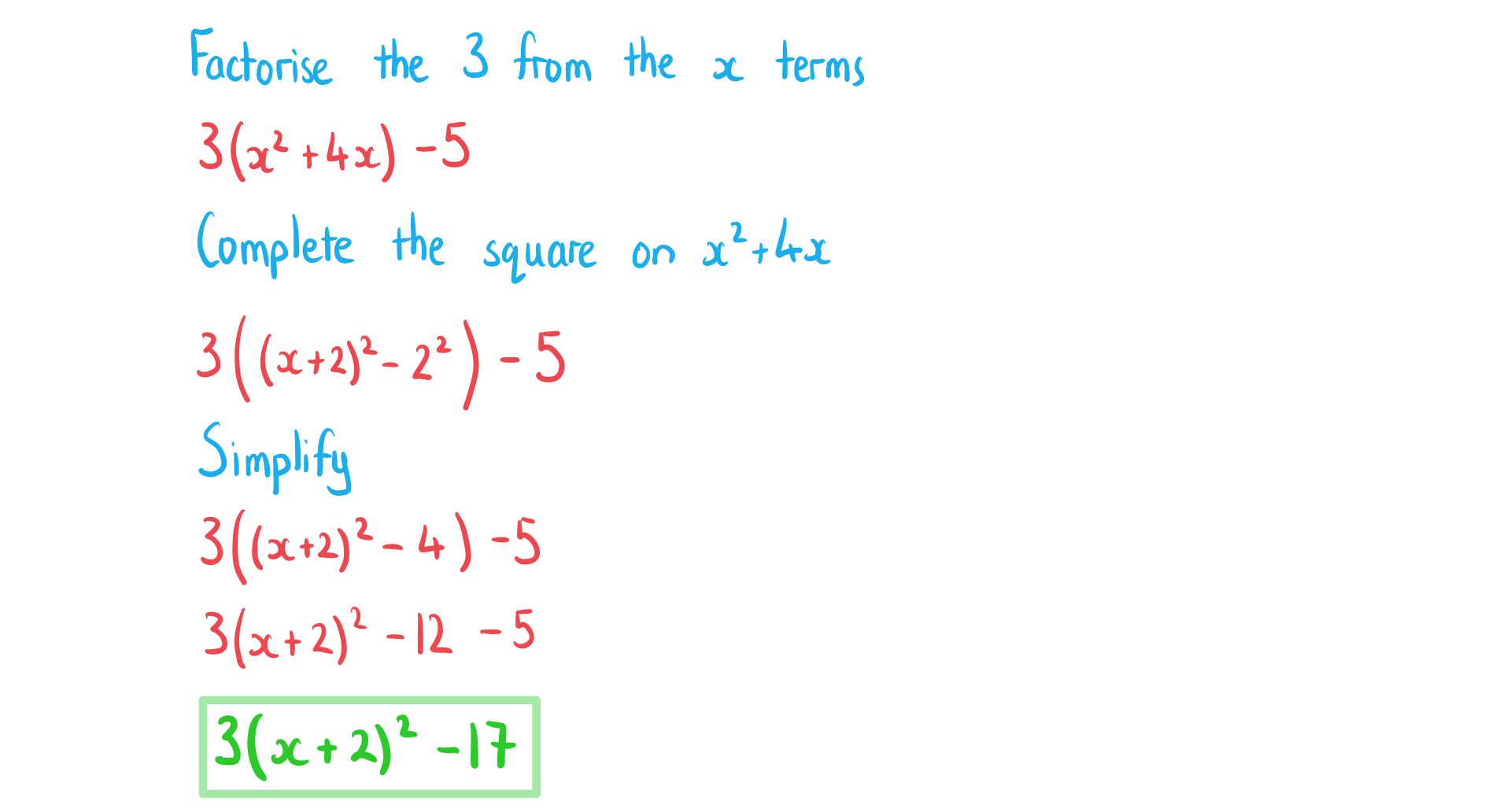

Unlock more, it's free!
Was this revision note helpful?
