Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)HLRevision Notes3. Geometry & TrigonometryVector PlanesShortest Distances with Planes

Shortest Distances with Planes (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

Did this video help you?

Shortest Distance Between a Point and a Plane

What is the shortest distance from a point to a plane?

  • The shortest distance from any point to a plane is always the perpendicular distance

    • Let capital pi be a plane with equation a x plus b y plus c z equals d  

    • Let P be a point that does not lie on the line

Diagram showing a line intersecting a plane, with arrow indicating the shortest distance from point P perpendicularly to the plane.
Example of the shortest distance between a point and a plane

Examiner Tips and Tricks

This skill is not explicitly stated in the syllabus guide. However, I have seen this come up in Paper 2 in the November 2022 exams. It was worth 5 marks!

How do I find the shortest distance between a point and a plane?

  • For example, consider

    • the line capital pi space colon space 2 x plus y minus 2 z equals 10

    • the point P open parentheses 11 comma space 9 comma space minus 12 close parentheses

  • STEP 1
    Find a normal vector to the plane

    • bold italic n equals open parentheses table row 2 row 1 row cell negative 2 end cell end table close parentheses

  • STEP 2
    Find an equation of a line that is perpendicular to the plane and passes through the point

    • bold italic r equals open parentheses table row 11 row 9 row cell negative 12 end cell end table close parentheses plus lambda open parentheses table row 2 row 1 row cell negative 2 end cell end table close parentheses

  • STEP 3
    Find the value of lambda at the point of intersection of this line and the plane

    • 2 open parentheses 11 plus 2 lambda close parentheses plus open parentheses 9 plus lambda close parentheses minus 2 open parentheses negative 12 minus 2 lambda close parentheses equals 10 rightwards double arrow lambda equals negative 5

  • STEP 4
    Multiply the normal vector by the value of lambda and find the magnitude

    • open vertical bar open parentheses negative 5 close parentheses open parentheses table row 2 row 1 row cell negative 2 end cell end table close parentheses close vertical bar equals 15

Examiner Tips and Tricks

This works because the point of intersection occurs when lambda equals 0. Therefore, the displacement vector from the point of intersection and the given point is lambda bold italic n. Alternatively, you could explicitly find the position vector f the point of intersection and then find the distance between that and the position vector of the given point.

How do I find the shortest distance between a given point on a line and a plane?

  • You can use the steps above

  • It might be quicker to use right-angled trigonometry if you also know the point of intersection and/or the angle between the line and the plane

    • The shortest length between the point and the plane is perpendicular to the line

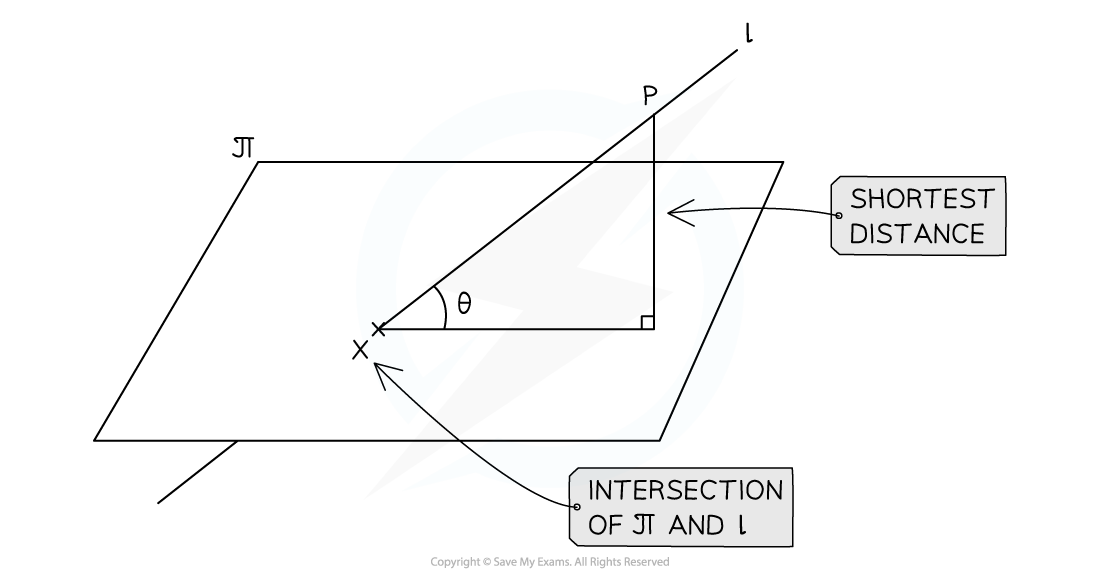
Diagram depicting a plane and a line with intersection at point X. Line L intersects at angle θ. Shortest distance line is shown as perpendicular.
Example of finding the shortest distance of a point on a line to a plane

How do I find the shortest distance between a plane and a line parallel to the plane?

  • Pick any point on the line

  • Find the shortest distance between that point and the plane

How do I find the shortest distance between two parallel planes?

  • Pick any point on one of the planes

  • Find the shortest distance between that point and the other plane

Examiner Tips and Tricks

Vector planes questions can be tricky to visualise, read the question carefully and sketch a very simple diagram to help you get started.

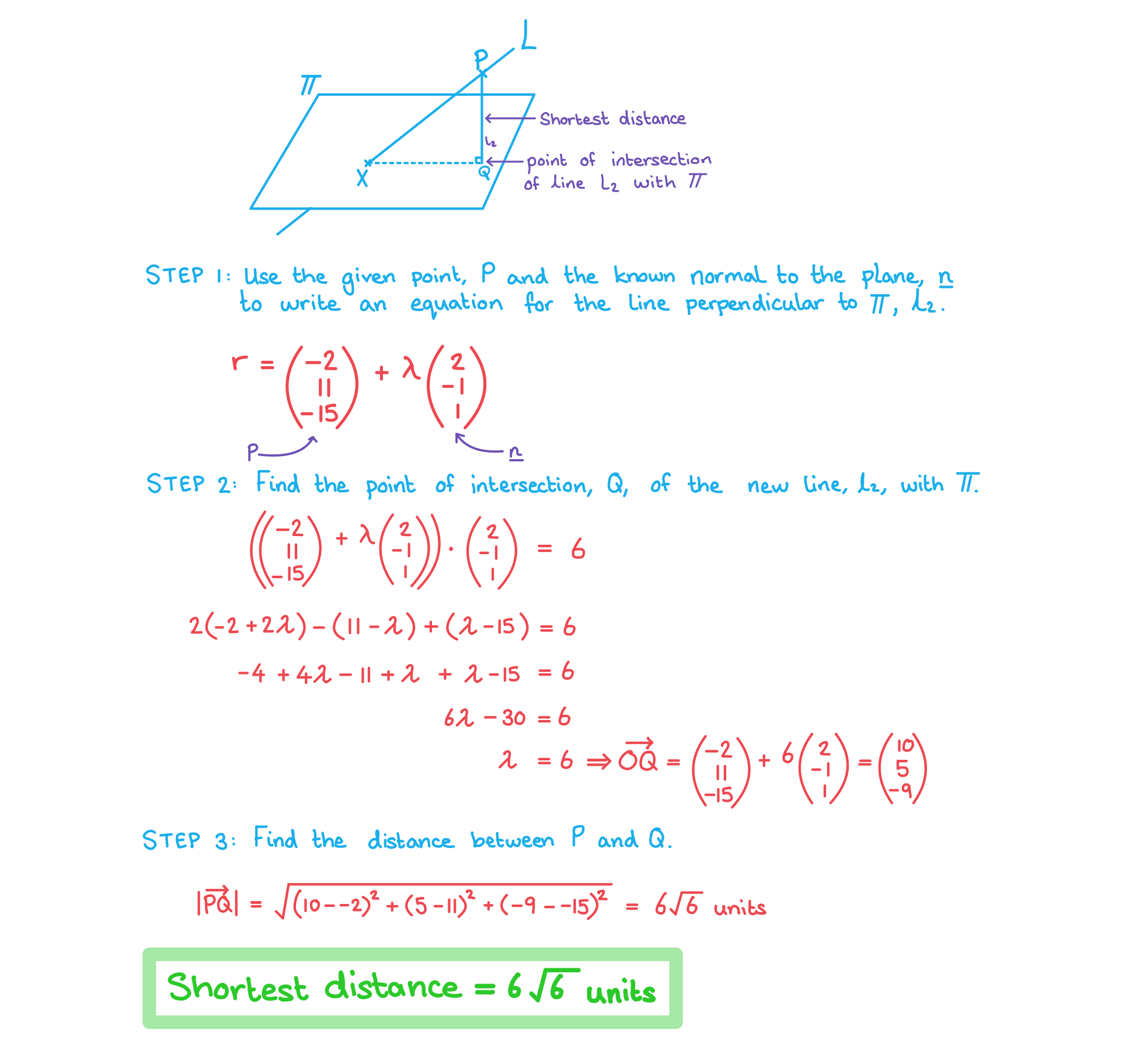
Worked Example

The plane capital pi has equation bold r times open parentheses table row 2 row cell negative 1 end cell row 1 end table close parentheses equals 6.

The line begin mathsize 16px style L end style has equation bold r equals open parentheses table row 2 row 3 row 1 end table close parentheses plus s open parentheses table row 1 row cell negative blank 2 end cell row 4 end table close parentheses.

The point P space left parenthesis negative 2 comma space 11 comma space minus 15 right parenthesis lies on the line begin mathsize 16px style L end style.

Find the shortest distance between the point P and the plane capital pi.

3-11-4-ib-hl-aa-shortest-dist-two-planes-we-1

Worked Example

Consider the parallel planes defined by the equations:

capital pi subscript 1 blank colon space space bold r times open parentheses table row 3 row cell negative 5 end cell row 2 end table close parentheses space equals space 44,

capital pi subscript 2 blank colon space space bold r bold space equals space open parentheses table row 0 row 0 row 3 end table close parentheses space plus space lambda open parentheses table row 2 row 0 row cell negative 3 end cell end table close parentheses space plus space mu open parentheses table row 1 row 1 row 1 end table close parentheses.

Find the shortest distance between the two planes begin mathsize 16px style capital pi subscript 1 end style and capital pi subscript 2.

3-11-4-ib-hl-aa-short-dist-two-planes-we-solution-2

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Angles Between Two PlanesNext:Sampling & Data Collection
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.