International A Level (IAL)PhysicsEdexcelRevision Notes4. Further Mechanics, Fields & ParticlesMomentum & ImpulseApplying Conservation of Linear Momentum

Applying Conservation of Linear Momentum (Edexcel International A Level (IAL) Physics): Revision Note

Exam code: YPH11

Katie M

Author

Katie M

Last updated

Applying Conservation of Linear Momentum

  • The principle of conservation of linear momentum states:

The total momentum before a collision = the total momentum after a collision provided no external force acts

  • Linear momentum is the momentum of an object that only moves in a straight line

  • Momentum is a vector quantity

    • This means oppositely-directed vectors can cancel each other out, resulting in a net momentum of zero

    • If, after a collision, an object starts to move in the opposite direction to which it was initially travelling, its velocity will now be negative

  • Momentum, just like energy, is always conserved

Conservation of Linear Momentum in 1D

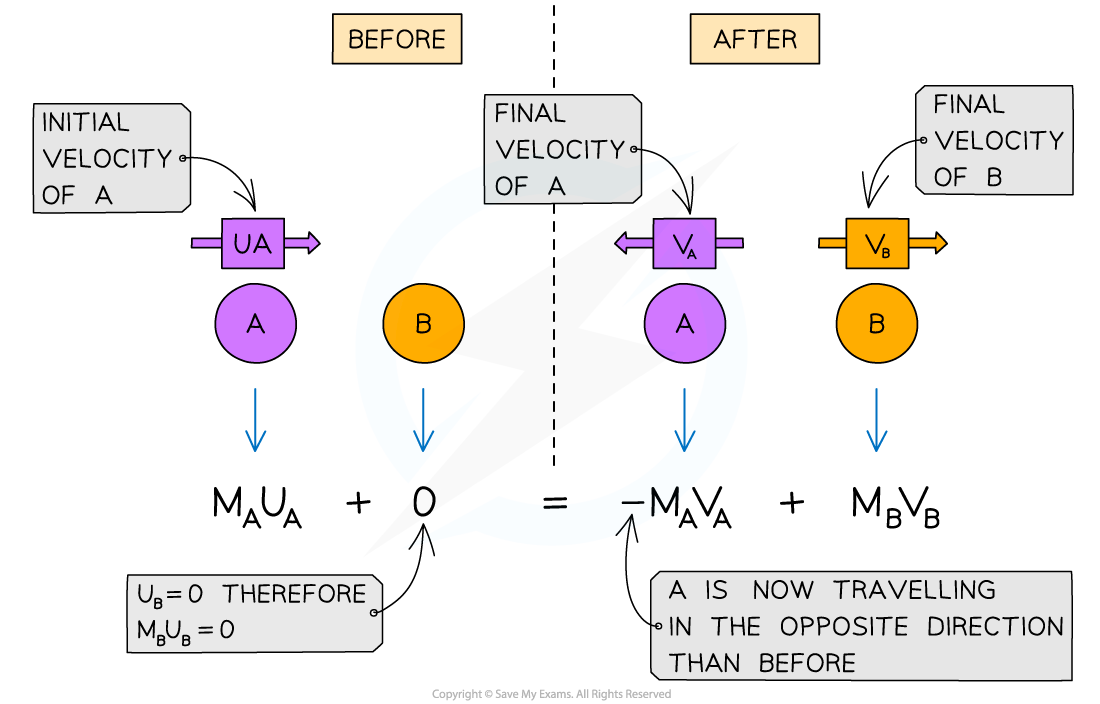
Conversation of Momentum, downloadable AS & A Level Physics revision notes

The conservation of momentum in 1D, for two objects A and B colliding then moving apart

Worked Example

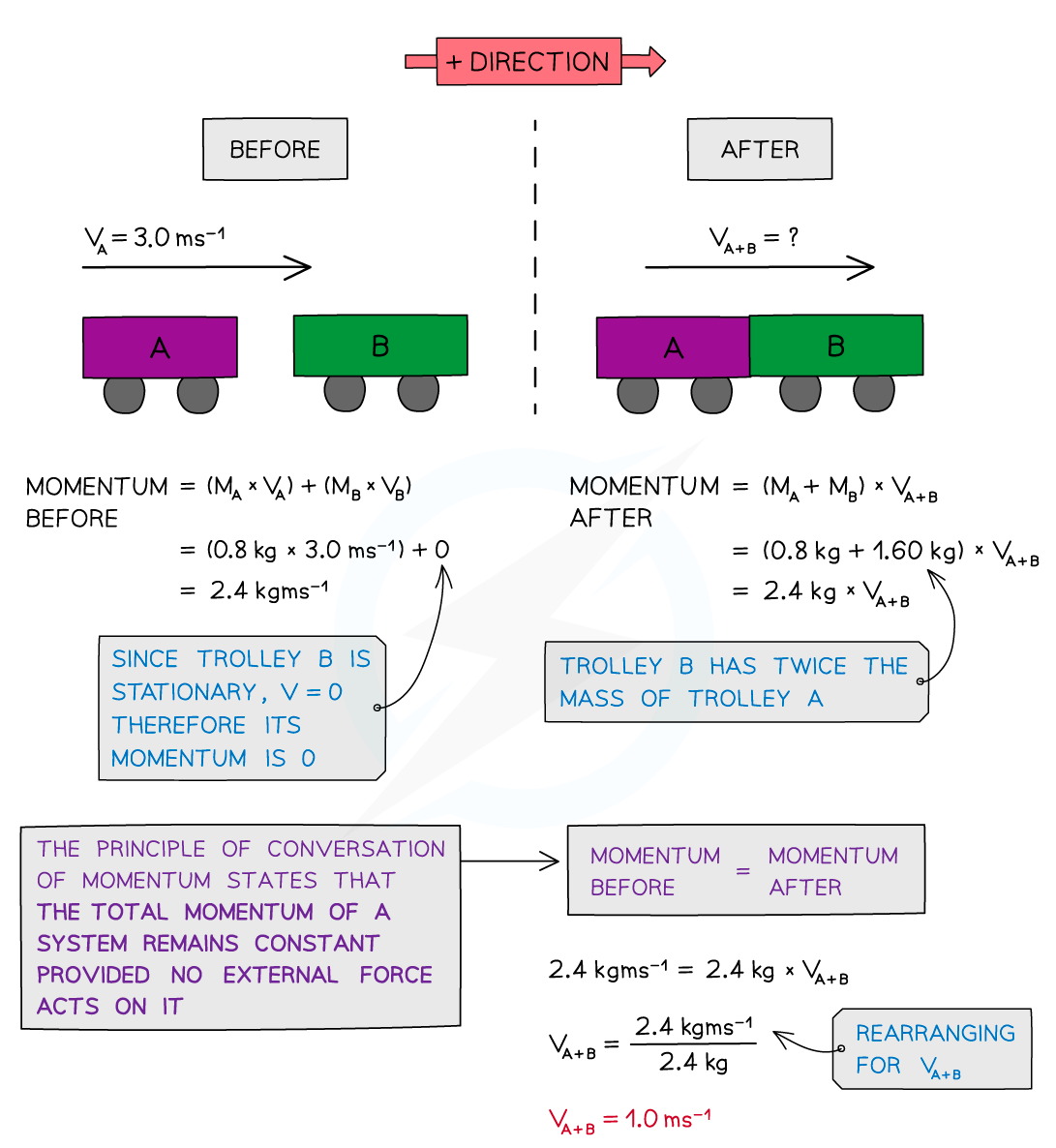
Trolley A of mass 0.80 kg collides head-on with stationary trolley B whilst travelling at 3.0 m s–1. Trolley B has twice the mass of trolley A. On impact, the trolleys stick together.

Using the conservation of momentum, calculate the common velocity of both trolleys after the collision.

Answer:

Worked example - 1D momentum quesions solution

Examiner Tips and Tricks

Momentum is a vector quantity, therefore, you should always define a direction to be 'positive' when applying the principle of conservation of momentum. In this worked example, we implicitly took velocity 'to the right' as the positive direction.

Sometimes, however, you might encounter two objects moving towards each other before colliding. If both objects have the same mass m and speed v, then the total momentum (before collision) is zero, because ptotal = (mv) + (–mv) = 0. Note the negative sign indicates a body travelling in the opposite direction. 

Conservation of Linear Momentum in 2D

  • For objects moving in 2D, there are components of momentum to consider

    • This is similar to projectile motion in 2D, in which we consider horizontal and vertical components of motion

Vector components

Vector R split into its vertical, R cos (30) and horizontal, R sin (30), components

  • Each component of momentum is conserved separately 

    • Since momentum is a vector, it can be resolved into horizontal and vertical components

    • The sum of horizontal components will be equal before and after a collision

    • The sum of vertical components will be equal before and after a collision

Worked Example

A red snooker ball, travelling at 2.5 m s–1, collides with a green snooker ball, which is at rest. Both snooker balls have the same mass m. 

The angle of collision is such that the red ball moves off at 28° below the horizontal at 2.1 m s–1 and the green ball moves off at 55° above the horizontal, with a speed v, as shown.

6-3-snooker-we_edexcel-al-physics-rn

Determine the size of v.

Answer:

Step 1: Apply the conservation of linear momentum in both directions

  • Since no external forces act during the collision, momentum is conserved in both the:

    • horizontal direction (x)

    • vertical direction (y)

  • This means that either of the following could be used: 

Total horizontal momentum before = total horizontal momentum after

Total vertical momentum before = total vertical momentum after

Step 2: Resolve the final velocities of the balls into components: 

  • For the red ball

    • horizontal velocity = 2.1 cos 28°

    • vertical velocity = -2.1 sin 28°

  • For the green ball

    • horizontal velocity = v cos 55°

    • vertical velocity = v sin 55°

Step 3: Set up a momentum equation in one of the directions

  • The equation will be simpler in the vertical direction since the total initial vertical momentum is zero

Total vertical momentum before = total vertical momentum after

m u subscript y red end subscript space plus space m u subscript y green end subscript space equals space m v subscript y red end subscript space plus space m v subscript y green end subscript

0 space plus space 0 space equals space m open parentheses negative 2.1 space sin space 28 degree close parentheses space plus space m open parentheses v space sin space 55 degree close parentheses

0 space equals space minus 2.1 space sin space 28 degree space plus space v space sin space 55 degree

Step 4: Simplify and rearrange to calculate v

v space sin space 55 degree space equals space 2.1 space sin space 28 degree

v space equals space fraction numerator 2.1 space sin space 28 degree over denominator sin space 55 degree end fraction space equals space 1.2 space straight m space straight s to the power of negative 1 end exponent

Examiner Tips and Tricks

Generally speaking, whenever you see any vector given at an angle to the horizontal or the vertical (e.g. velocity, or momentum), think "resolve"! It's extremely likely you will need to consider the separate components of motion for a projectiles question or for a conservation of momentum question. 

Questions which ask you to use the principle of conservation of linear momentum in 2D are usually worth a lot of marks, so make sure you practise lots of questions involving resolving vectors! 

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Core Practical 9: Investigating ImpulseNext:Core Practical 10: Investigating Collisions using ICT
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.