National 5MathsSQARevision NotesAlgebraic SkillsEquation of a Straight Liney-b=m(x-a)

y-b=m(x-a) (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Determining the equation of a straight line

What is the equation of a straight line?

  • The general equation of a straight line is y = mx + c  where

    • m  is the gradient

    • c  is the y-intercept

      • The value where the line cuts the y-axis

  • y  = 5x  + 2  is a straight line with

    • gradient 5

    • y-intercept 2

  • y  = 3 - 4x  is a straight line with

    • gradient -4

    • y-intercept 3

How do I find the equation of a straight line using y-b=m(x-a)?

  • To find the equation of a line you need to know

    • The coordinates of a point on the line

    • The gradient of the line

      • If you know two points on the line, open parentheses x subscript 1 comma space y subscript 1 close parentheses and open parentheses x subscript 2 comma space y subscript 2 close parentheses

      • You can find the gradient using the formula gradient equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction

  • If the line has gradient m and goes through the point (a, b)

    • then an equation of the line is y - b = m(x - a)

    • E.g. the line with gradient 3 through point (2, 5)

      • m equals 3, a equals 2, b equals 5

      • An equation of the line is space y minus 5 equals 3 open parentheses x minus 2 close parentheses

  • An equation in this form can be rearranged into y = mx + c form if required:

table row cell space y minus 5 end cell equals cell 3 open parentheses x minus 2 close parentheses end cell row cell y minus 5 end cell equals cell 3 x minus 6 end cell row y equals cell 3 x minus 6 plus 5 end cell row y equals cell 3 x minus 1 end cell end table

How do I find the equation of a straight line using y=mx+c?

  • You can also use y = mx + c to find the equation of a line, if you know the gradient m and a point on the line (a, b)

  • Substitute the values of m and (x, y) = (a, b) into the equation

    • Then solve to find the value of c

  • E.g. the line with gradient 3 through point (2, 5)

    • m equals 3, open parentheses x comma space y close parentheses equals open parentheses 2 comma space 5 close parentheses

      • Substituting into space y equals m x plus cgives space 5 equals 3 open parentheses 2 close parentheses plus c

      • So space 5 equals 6 plus c space rightwards double arrow space c equals negative 1

    • The equation of the line is space y equals 3 x minus 1

How do I find the equation of a straight line from a graph?

  • Find the gradient m by drawing a triangle and using

    • gradient equals rise over run

      • Positive for uphill lines, negative for downhill

  • Read off the y-intercept c from the graph

    • Where it cuts the y-axis

  • Substitute these values into y  = mx  + c 

What if no y-intercept is shown on the graph?

  • If you can't read off the y-intercept

    • Find any point on the line

    • Use one of the methods above to find the equation

What are the equations of horizontal and vertical lines?

  • A horizontal line has the equation y  = c

    • c  is the y-intercept

  • A vertical line has the equation x  = k

    •  k  is the x-intercept

  • For example

    • y = 4

    • x = -2

Worked Example

The diagram shows the straight line passing through points A and B.

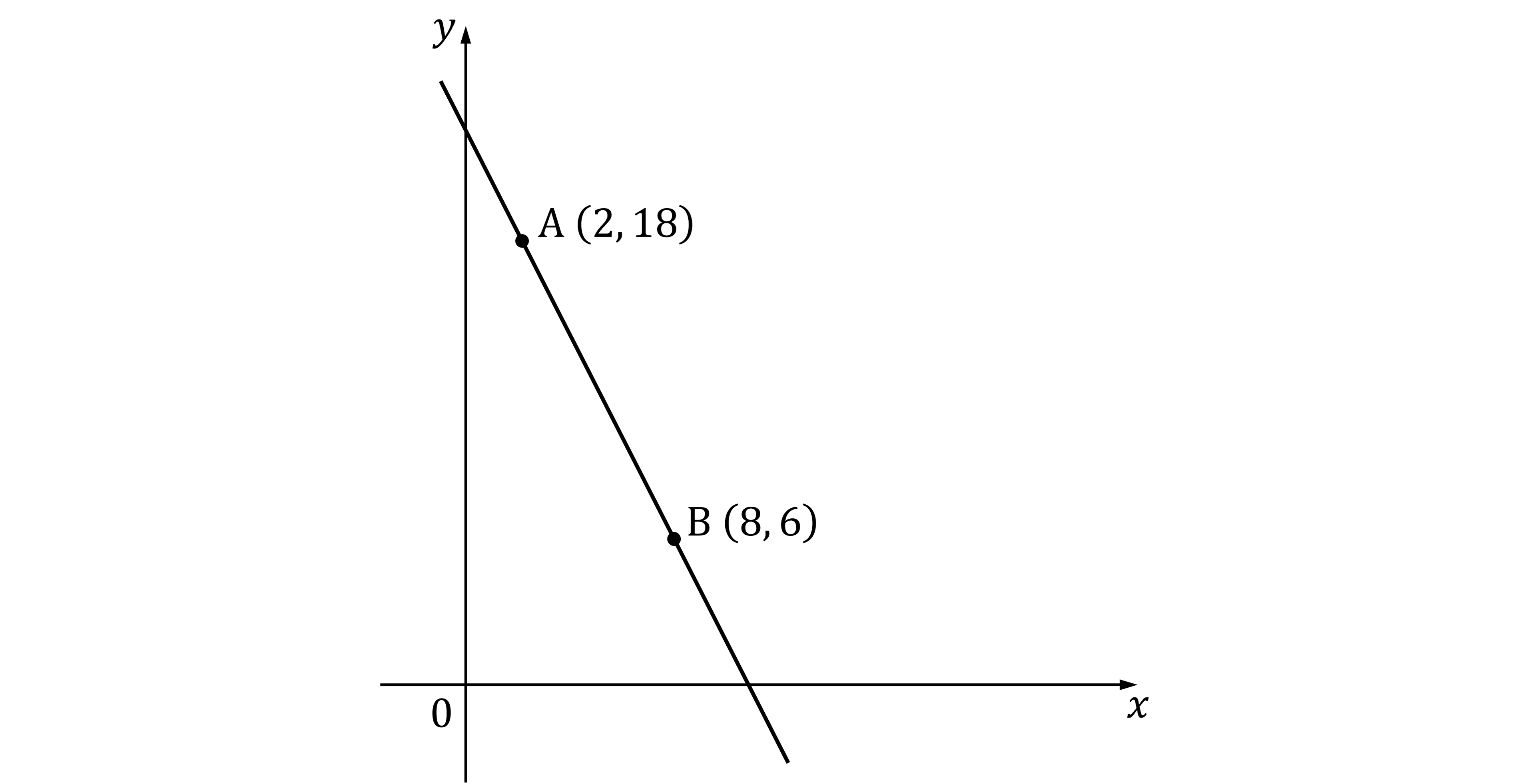
Graph with x and y axes. A line passes through points A (2, 18) and B (8, 6), sloping downwards from left to right.

Find the equation of the line AB.

Give the equation in its simplest form.

Answer:

Find m, the gradient of the line, using space gradient equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction

  • open parentheses x subscript 1 comma space y subscript 1 close parentheses equals open parentheses 2 comma space 18 close parentheses

  • open parentheses x subscript 2 comma space y subscript 2 close parentheses equals open parentheses 8 comma space 6 close parentheses

space gradient equals fraction numerator 6 minus 18 over denominator 8 minus 2 end fraction equals fraction numerator negative 12 over denominator 6 end fraction equals negative 2

The slope of the line is downward from left to right

  • So the negative gradient is as expected
     

Method 1

Use space y minus b equals m open parentheses x minus a close parentheses with

  • m equals negative 2

  • open parentheses a comma space b close parentheses equals open parentheses 2 comma space 18 close parentheses

    • open parentheses a comma space b close parentheses equals open parentheses 8 comma space 6 close parentheses would also work, and would lead to the same answer

space y minus 18 equals negative 2 open parentheses x minus 2 close parentheses

Simplify the equation into space y equals m x plus c form

table row cell space y minus 18 end cell equals cell negative 2 x plus 4 end cell row y equals cell negative 2 x plus 4 plus 18 end cell row y equals cell negative 2 x plus 22 end cell end table

That is the equation in simplest form

y equals negative 2 x plus 22
 

Method 2

Use space y equals m x plus c with

  • m equals negative 2

  • open parentheses x comma space y close parentheses equals open parentheses 2 comma space 18 close parentheses

    • open parentheses x comma space y close parentheses equals open parentheses 8 comma space 6 close parentheses would also work, and would lead to the same answer

table row cell space y end cell equals cell m x plus c end cell row 18 equals cell negative 2 open parentheses 2 close parentheses plus c end cell end table

Solve to find the value of c

table row 18 equals cell negative 4 plus c end cell row cell 18 plus 4 end cell equals c row 22 equals c end table

Substitute that back into space y equals m x plus c with m equals negative 2

space y equals negative 2 x plus 22

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Gradient of a LineNext:Algebraic Solution to Simultaneous Equations
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.