National 5MathsSQARevision NotesAlgebraic SkillsQuadratic FunctionsFeatures of Quadratic Graphs

Features of Quadratic Graphs (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Turning point & axis of symmetry of a quadratic graph

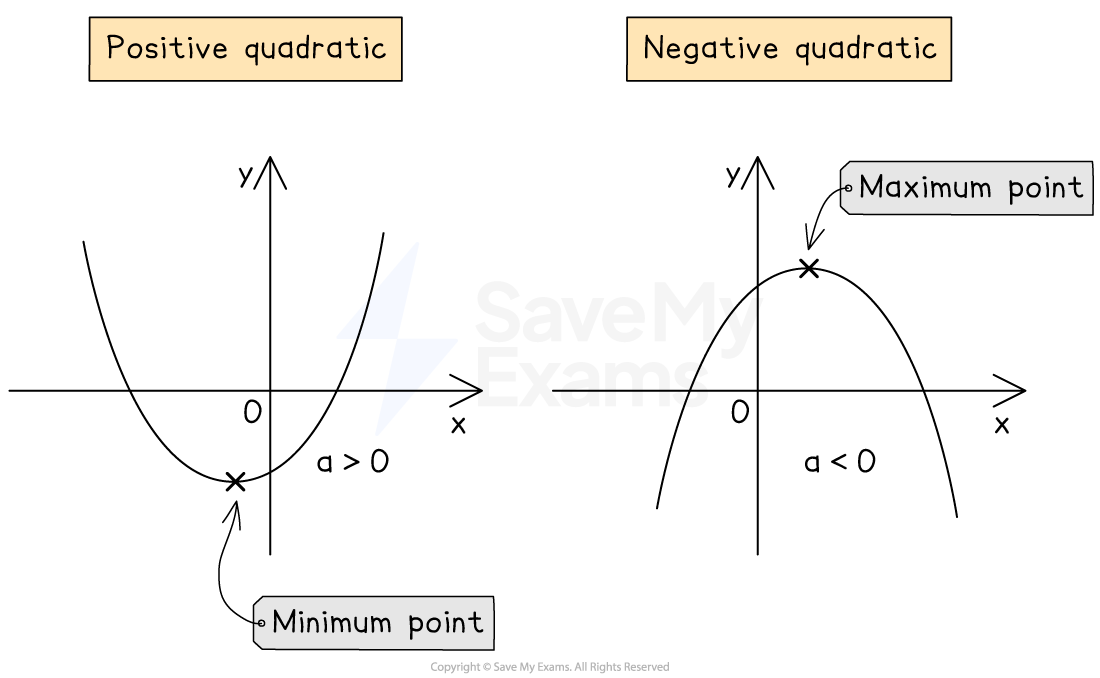
What does a quadratic graph look like?

  • A quadratic graph is a smooth curve with a vertical axis of symmetry

  • If the the equation of the graph is given in the form y equals a x squared plus b x plus c, then

    • A positive number in front of x squared gives a bold union-shaped curve

    • A negative number in front of x squared gives a bold intersection-shaped curve

  • The shape made by a quadratic graph is known as a parabola

  • A quadratic graph will always cross the y-axis

  • A quadratic graph intersects the x-axis twice, once, or not at all

    • The points where the graph intersects the x-axis are called the roots

  • If the graph is a bold union-shape, then it has a minimum point

  • If the graph is a bold intersection-shape, then it has a maximum point

  • Minimum and maximum points are both examples of turning points

    • The turning point of a parabola is sometimes also referred to as its vertex

Diagram showing a positive quadratic curve with a minimum point and a negative quadratic curve with a maximum point.

How can I find the turning point and axis of symmetry of a quadratic graph?

  • The easiest way to find the turning point and axis of symmetry of a quadratic graph is by completing the square on its equation

    • On such questions in the exam the equation will be given to you in the form y equals x squared plus p x plus q

  • Complete the square to rewrite the quadratic in the form y equals open parentheses x plus a close parentheses squared plus b

    • If y equals open parentheses x plus a close parentheses squared plus b then the turning point is at open parentheses negative a comma space b close parentheses

      • Notice the negative sign with the x-coordinate

    • This can also help you create the equation of a quadratic when given the turning point

  • The axis of symmetry of a quadratic graph always goes through the turning point

    • So if the turning point is open parentheses negative a comma space b close parentheses, then the axis of symmetry is x equals negative a

Completing the square Notes Diagram 3, A Level & AS Level Pure Maths Revision Notes

Worked Example

(a) Express x squared plus 10 x plus 7 in the form open parentheses x plus a close parentheses squared plus b.

(b) Hence, or otherwise, state the coordinates of the turning point of the graph of y equals x squared plus 10 x plus 7.

The diagram shows the graph of y equals x squared plus 10 x plus 7.

A line PQ has been drawn parallel to the x-axis, where:

  • P lies on the y-axis

  • P and Q lie on the graph of y equals x squared plus 10 x plus 7.

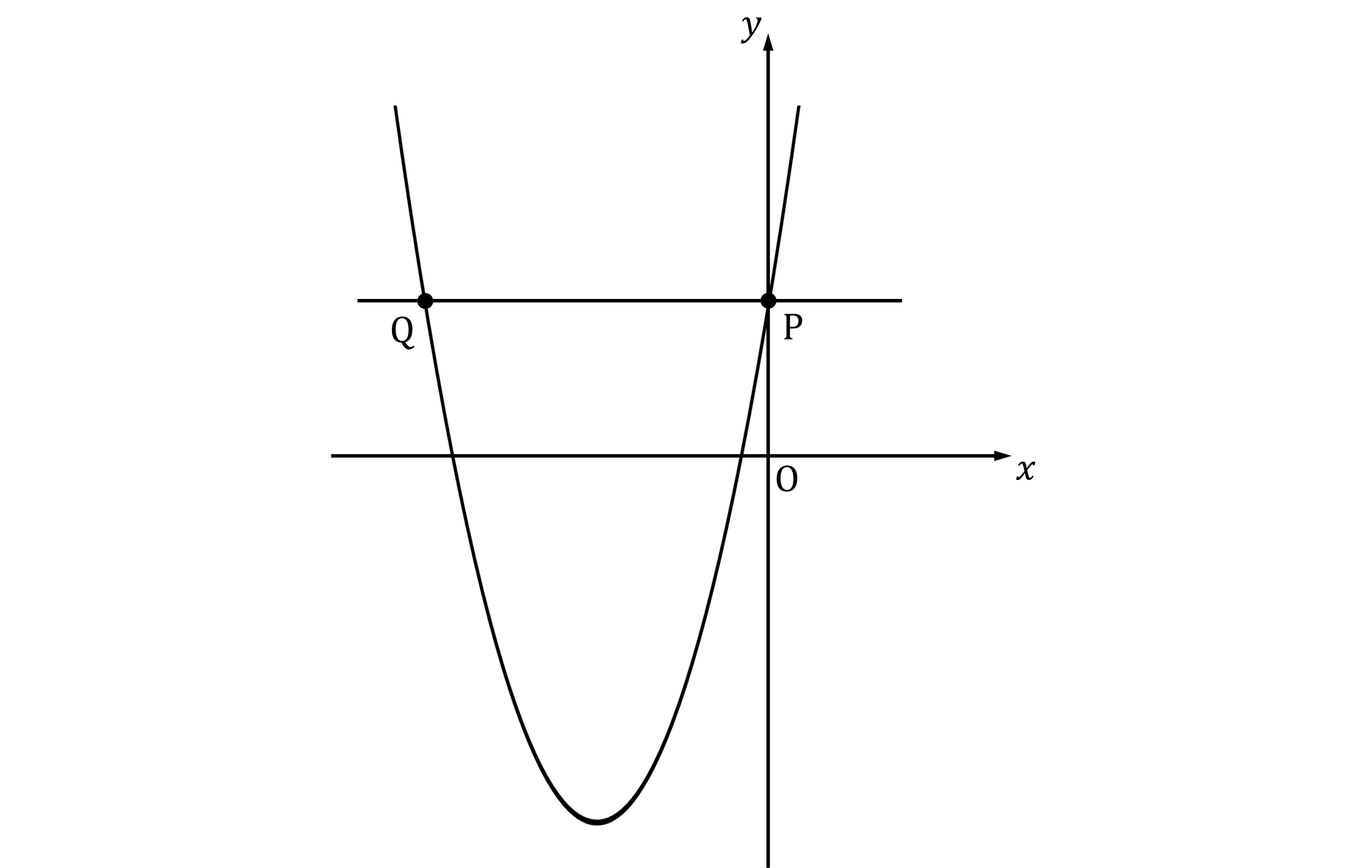
Graph of a parabola opening upwards, intersecting the y-axis at point P. A horizontal line intersects the parabola at points P and Q. Axes are labelled x and y with origin at O.

(c) Find the coordinates of Q.

Answer:

Part (a)

Use x squared plus p x equals open parentheses x plus p over 2 close parentheses squared minus open parentheses p over 2 close parentheses squared to rewrite x squared plus 10 x

  • Here space p equals 10, so p over 2 equals 5

table row cell x squared plus 10 x end cell equals cell open parentheses x plus 5 close parentheses squared minus 5 squared end cell row blank equals cell open parentheses x plus 5 close parentheses squared minus 25 end cell end table

Substitute that back into the original expression

table row cell x squared plus 10 x minus 17 end cell equals cell open parentheses x plus 5 close parentheses squared minus 25 plus 7 end cell row blank equals cell open parentheses x plus 5 close parentheses squared minus 18 end cell end table

table row blank blank cell open parentheses x plus 5 close parentheses squared minus 18 end cell end table

Part (b)

Use the fact that if y equals open parentheses x plus a close parentheses squared plus b then the turning point is at open parentheses negative a comma space b close parentheses

  • Don't forget the negative sign with the x-coordinate!

open parentheses negative 5 comma space minus 18 close parentheses

Part (c)
Answering this part of the question relies on the symmetry of the parabola

From part (b), you know that the turning point is open parentheses negative 5 comma space minus 18 close parentheses

  • That means the axis of symmetry is at x equals negative 5

Point P is the y-axis intercept of the parabola, with x-coordinate 0

  • You can find its y-coordinate by substituting x equals 0 into the equation of the curve

y equals open parentheses 0 close parentheses squared plus 10 open parentheses 0 close parentheses plus 7 equals 7

So the coordinates of point P are open parentheses 0 comma space 7 close parentheses

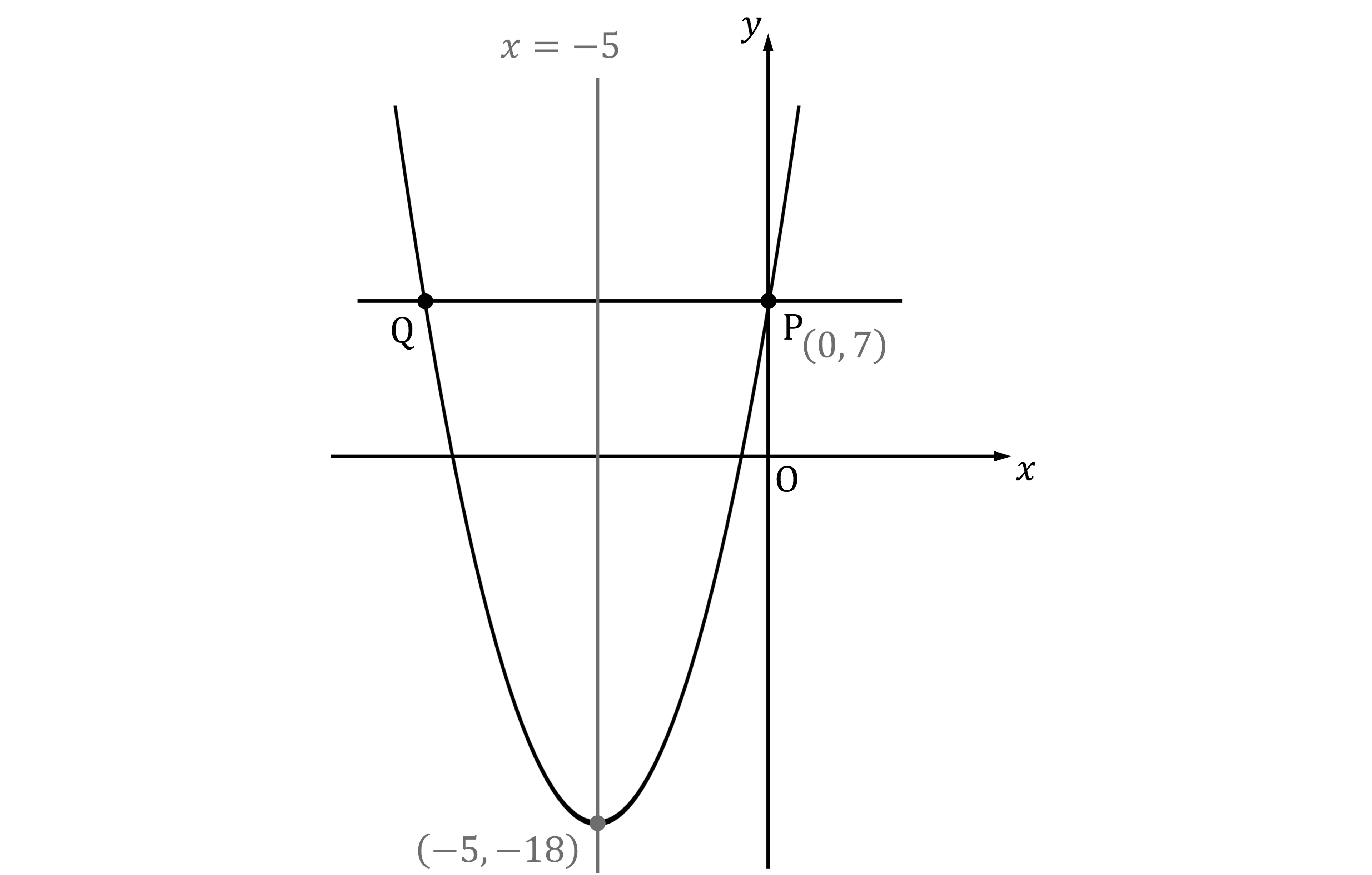
Graph of a parabola opening upwards, intersecting the y-axis at point P. A horizontal line intersects the parabola at points P and Q. The turning point of the parabola has been labelled (-5, -18), and the vertical line x=-5 has been drawn through it. Point P has been labelled (0-, 7). Axes are labelled x and y with origin at O.

Line PQ is parallel to the x-axis

  • So P and Q have the same y coordinate

And point P is 5 units to the right of the axis of symmetry

  • So by the symmetry point Q will be five units to the left of the axis of symmetry

Point Q has coordinates (-10, 7)

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:DiscriminantNext:Equation of a Quadratic Graph
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.