National 5MathsSQARevision NotesAlgebraic SkillsQuadratic FunctionsSketching Quadratics

Sketching Quadratics (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Sketching quadratics y = (ax - m)(bx - n)

What is the connection between the solutions of a quadratic equation and the corresponding quadratic graph?

  • There is an important connection between

    • the quadratic graph of y equals a x squared plus b x plus c

    • and the solutions of the corresponding quadratic equation a x squared plus b x plus c equals 0

  • If x equals p is a solution to a x squared plus b x plus c equals 0

    • then the graph of y equals a x squared plus b x plus c intercepts the bold italic y-axis at open parentheses p comma space 0 close parentheses

    • Remember that y equals 0 is the equation of the x-axis

  • This means you can use a quadratic graph to find solutions to the corresponding quadratic equation

    • The x-coordinates of its x-axis intercepts (if any) are the solutions to the equation

  • It also means you can use the solutions to a quadratic equation to determine features of the corresponding quadratic graph

    • For example if the equation has two distinct solutions, then the graph intersects the x-axis at two points

    • If the equation only has one solution, then the graph only touches the x-axis at a single point

    • If the equation has no solutions, then the graph does not intersect the x-axis (it is either wholly above or wholly below it)

How do I sketch a quadratic graph from an equation in factorised form?

  • It is easy to sketch the graph of a quadratic if its equation is given in factorised form y equals open parentheses a x minus m close parentheses open parentheses b x minus n close parentheses

  • For example, to sketch the graph of y equals open parentheses 2 x minus 1 close parentheses open parentheses 2 x minus 7 close parentheses

    • Solve open parentheses 2 x minus 1 close parentheses open parentheses 2 x minus 5 close parentheses equals 0 by setting the brackets equal to zero and solving

      • 2 x minus 1 equals 0 space space rightwards double arrow space space x equals 0.5

      • 2 x minus 7 equals 0 space space rightwards double arrow space space x equals 3.5

      • So the quadratic intercepts the bold italic x-axis at open parentheses 0.5 comma space 0 close parentheses and open parentheses 3.5 comma space 0 close parentheses

    • The axis of symmetry occurs midway between the x-axis intercepts

      • fraction numerator 0.5 plus 3.5 over denominator 2 end fraction equals 4 over 2 equals 2

      • So the axis of symmetry is x equals 2

    • The turning point lies on the axis of symmetry

      • Substitute x equals 2 into the equation

      • y equals open parentheses 2 open parentheses 2 close parentheses minus 1 close parentheses open parentheses 2 open parentheses 2 close parentheses minus 7 close parentheses equals 3 cross times open parentheses negative 3 close parentheses equals negative 9

      • So the turning point is at open parentheses 2 comma space minus 9 close parentheses

    • The bold space bold italic y-axis intercept occurs when x equals 0

      • Substitute x equals 0 into the equation

      • y equals open parentheses 2 open parentheses 0 close parentheses minus 1 close parentheses open parentheses 2 open parentheses 0 close parentheses minus 7 close parentheses equals open parentheses negative 1 close parentheses cross times open parentheses negative 7 close parentheses equals 7

      • So the space y-axis intercept is at open parentheses 0 comma space 7 close parentheses

    • That is all you need to sketch the graph!

      • If the turning point is below the x-axis (i.e. has a negative y-coordinate)

        • then the parabola is union-shaped

      • If the turning point is above the x-axis (i.e. has a positive y-coordinate)

        • then the parabola is intersection-shaped

Examiner Tips and Tricks

A sketch does not need to be 'perfect' or 'to scale', it just needs to show the main features of the graph:

  • Smooth parabola that is correctly shown as union-shaped or intersection-shaped

  • Axis intercepts and turning point labelled, and drawn on the correct sides of the x- and y-axes

Worked Example

Sketch the graph of y equals open parentheses x plus 3 close parentheses open parentheses x minus 1 close parentheses using the axes provided below.

On your sketch, show clearly the points of intersection with the x-axis and the y-axis, and the coordinates of the turning point.

Cartesian coordinate system with horizontal x-axis and vertical y-axis intersecting at origin point labelled O. Arrows indicate positive directions.

Answer:

The roots will be the solutions to y equals 0

open parentheses x plus 3 close parentheses open parentheses x minus 1 close parentheses equals 0

The two solutions will be the solutions of each bracket set equal to zero

open parentheses x plus 3 close parentheses equals 0 space space rightwards double arrow space space x equals negative 3

open parentheses x minus 1 close parentheses equals 0 space space rightwards double arrow space space x equals 1

That lets you know the graph will cross the x-axis at x equals negative 3 and x equals 1

The intersection with the y-axis will occur when x equals 0

table row y equals cell open parentheses 0 plus 3 close parentheses open parentheses 0 minus 1 close parentheses equals 3 cross times open parentheses negative 1 close parentheses equals negative 3 end cell end table

So the graph will cross the y-axis at y equals negative 3

Because a quadratic graph is symmetric, the x-coordinate of the turning point will be halfway between the two x-axis intercepts

  • So the x-coordinate of the turning point will be

x equals fraction numerator negative 3 plus 1 over denominator 2 end fraction equals fraction numerator negative 2 over denominator 2 end fraction equals negative 1

To find the y-coordinate, substitute x equals negative 1 into the equation for the curve

y equals open parentheses negative 1 plus 3 close parentheses open parentheses negative 1 minus 1 close parentheses equals 2 cross times open parentheses negative 2 close parentheses equals negative 4

So the turning point is at open parentheses negative 1 comma space minus 3 close parentheses

Draw a smooth quadratic curve that shows those axis intercepts and the turning point

  • It will be an 'up' or union-shaped parabola, because the first term if you expand open parentheses x minus 6 close parentheses open parentheses x plus 4 close parentheses is x squared

  • Be sure to label the coordinates for the three axis intercepts and the turning point

Graph of a parabola opening upwards, vertex at (-1, -4) marked. Graph intercepts x-axis at -3 and 1, and intercepts y-axis at -3. The x-axis and y-axis are labelled.

Sketching quadratics y = k(x + p)² + q

How do I sketch a quadratic graph from an equation in completed square form?

  • It is easy to sketch the graph of a quadratic if its equation is given in completed square form y equals k open parentheses x plus p close parentheses squared plus q

  • For example, to sketch the graph of y equals 2 open parentheses x minus 4 close parentheses squared plus 1

    • The turning point of y equals k open parentheses x plus p close parentheses squared plus q is at open parentheses negative p comma space q close parentheses

      • So the turning point of y equals 2 open parentheses x minus 4 close parentheses squared plus 1 is at open parentheses 4 comma space 1 close parentheses

    • The bold space bold italic y-axis intercept occurs when x equals 0

      • Substitute x equals 0 into the equation

      • y equals 2 open parentheses 0 minus 4 close parentheses squared plus 1 equals 2 open parentheses negative 4 close parentheses squared plus 1 equals 2 cross times 16 plus 1 equals 33

      • So the space y-axis intercept is at open parentheses 0 comma space 33 close parentheses

    • The number in front of the bracket, k, tells you the shape of the parabola

      • If k is positive, the parabola is union-shaped

      • If k is negative, the parabola is intersection-shaped

      • So y equals 2 open parentheses x minus 4 close parentheses squared plus 1 is union-shaped

    • That is all you need to sketch the graph!

      • Note that y equals 2 open parentheses x minus 4 close parentheses squared plus 1

        • is union-shaped

        • and has its turning point above the x-axis at open parentheses 0 comma space 33 close parentheses

      • That means that it will not intercept the x-axis

  • If you need to find bold italic x-axis intercepts for a quadratic in y equals k open parentheses x plus p close parentheses squared plus q form, you will need to set the quadratic equal to zero and then solve for x

    • For example, for y equals 2 open parentheses x minus 4 close parentheses squared minus 18:
      table row blank blank blank row cell space space space space space space space space space space space space space space space space space space space space space space space space 2 open parentheses x minus 4 close parentheses squared minus 18 end cell equals 0 row cell 2 open parentheses x minus 4 close parentheses squared end cell equals 18 row cell open parentheses x minus 4 close parentheses squared end cell equals 9 row cell x minus 4 end cell equals cell plus-or-minus square root of 9 end cell row cell x minus 4 end cell equals cell plus-or-minus 3 end cell row x equals cell 4 plus-or-minus 3 end cell row x equals cell 1 space or space 7 end cell row blank blank blank end table

    • The x-axis intercepts are at open parentheses 1 comma space 0 close parentheses and open parentheses 7 comma space 0 close parentheses

Worked Example

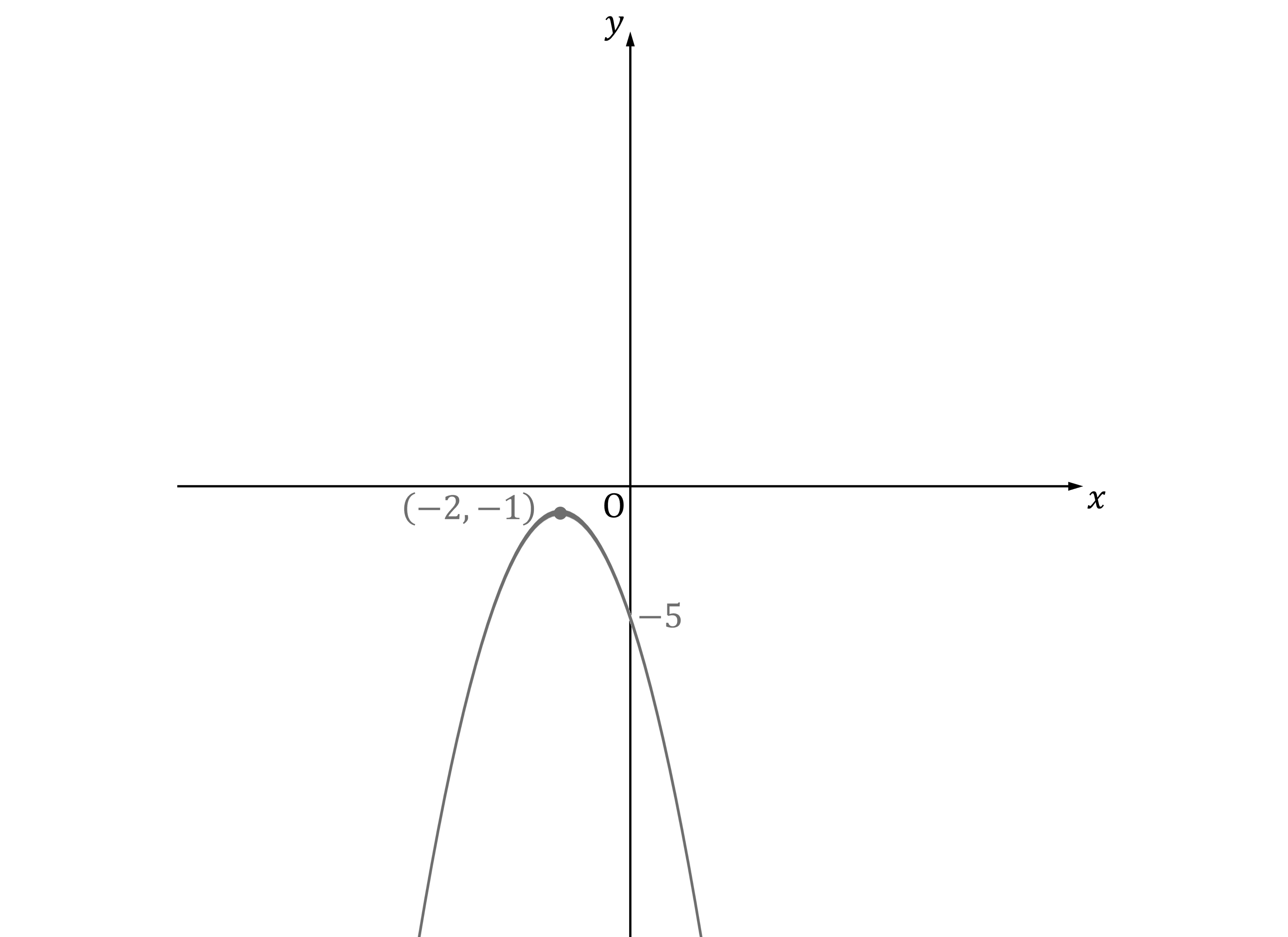
Sketch the graph of y equals negative open parentheses x plus 2 close parentheses squared minus 1 using the axes provided below.

On your sketch, show clearly the coordinates of the turning point, as well as any points of intersection with the coordinate axes.

Cartesian coordinate system with horizontal x-axis and vertical y-axis intersecting at origin point labelled O. Arrows indicate positive directions.

Answer:

Compare it to the standard form y equals k open parentheses x plus p close parentheses squared plus q with turning point at open parentheses negative p comma space q close parentheses

turning point at open parentheses negative 2 comma space minus 1 close parentheses

The intersection with the y-axis will occur when x equals 0

table row y equals cell negative open parentheses 0 plus 2 close parentheses squared minus 1 equals negative open parentheses 2 close parentheses squared minus 1 equals negative 4 minus 1 equals negative 5 end cell end table

So the graph will cross the y-axis at y equals negative 5

Draw a smooth quadratic curve that shows that y-axis intercepts and the turning point

  • It will be a 'down' or intersection-shaped parabola, because there is a negative sign in front of the bracket

  • The turning point is below the x-axis, so because of its shape the parabola will not intersect the x-axis

Graph of a parabolic curve with a vertex at (-2, -1), and y-intercept at -5. The x and y axes are labelled.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Equation of a Quadratic GraphNext:Arcs & Sectors
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.