National 5MathsSQARevision NotesGeometric SkillsCircle GeometryArcs & Sectors

Arcs & Sectors (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Calculating the length of an arc

What is an arc?

  • An arc is a part of the circumference of a circle 

  • Two points on a circumference of a circle will create two arcs 

    • The smaller arc is known as the minor arc

    • The bigger arc is known as the major arc

  • Radii from the centre of the circle to the two points will create an angle at the centre of the circle

    • This angle is often labelled by the Greek letter theta (theta)

How do I find the length of an arc?

Examiner Tips and Tricks

From your National 4 Maths course, you should be familiar with the formula for the circumference, C, of a circle with radius r:

C equals 2 pi r

Make sure you know this, as it is not given to you in the Formulae List on the exam paper.

  • Arc length is calculated using the formula space Arc space length equals theta over 360 cross times 2 pi r

    • r is the radius

    • theta is the angle at the centre

  • Note that this is just the fraction theta over 360 of the full circumference of the circle 2 pi r

  • To calculate the length of an arc:

    • STEP 1
      Divide the angle by 360 to form a fraction

      • theta over 360

    • STEP 2
      Calculate the circumference of the full circle

      • 2 pi r

    • STEP 3
      Multiply the fraction by the circumference

      • theta over 360 cross times 2 pi r

Sector Area & Arc Length Formulae

Worked Example

The diagram below shows a sector of a circle, centre straight C.

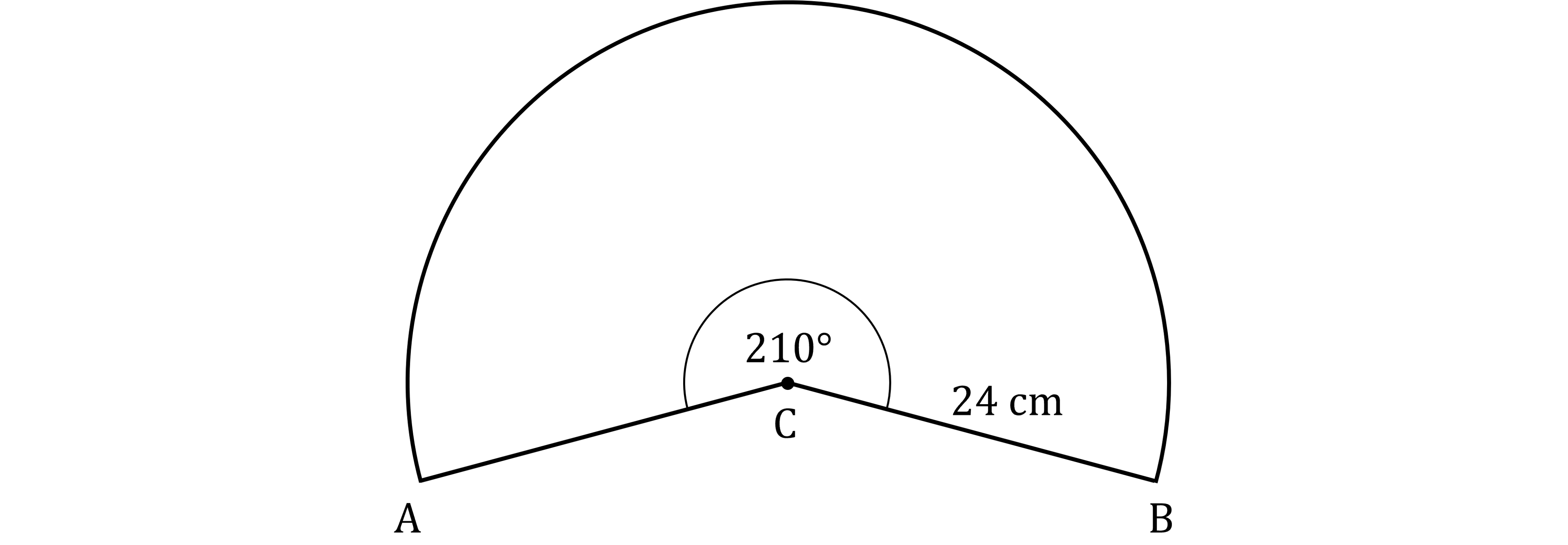
A circle sector with centre C, angle 210 degrees, and radius measuring 24 cm. Points A and B mark the ends of the sector's arc.

The radius of the circle is 24 centimetres.

Calculate the length of the major arc AB.

Give your answer correct to one decimal place.

Answer:

Divide the angle by 360 to form a fraction

  • Here space theta equals 210 degree

theta over 360 equals 210 over 360

Use C equals 2 pi r to find the circumference of the full circle

  • Here r equals 24

2 pi r equals 2 pi cross times 24

Multiply the fraction by the circumference

  • This is the same as substituting space theta equals 210 and r equals 24 into the formula arc space length equals theta over 360 cross times 2 pi r

  • If you remember that formula you can skip right to this step!

 arc space length equals 210 over 360 cross times 2 pi cross times 24

Use your calculator to work out that value 

equals 87.964594...

Round your answer to 1 decimal place, as required

88.0 cm (1 d.p.)

Calculating the area of a sector

What is a sector?

  • A sector is the part of a circle enclosed by two radii (radiuses) and an arc

    • A sector looks like a slice of a circular pizza

    • The curved edge of a sector is the arc

  • Two radii in a circle will create two sectors

    • The smaller sector is known as the minor sector

    • The bigger sector is known as the major sector

How do I find the area of a sector?

Examiner Tips and Tricks

From your National 4 Maths course, you should be familiar with the formula for the area, A, of a circle with radius r:

A equals pi r squared

Make sure you know this, as it is not given to you in the Formulae List on the exam paper.

  • Sector area is calculated using the formula space Sector space area equals theta over 360 cross times pi r squared

    • r is the radius

    • theta is the angle at the centre

  • Note that this is just the fraction theta over 360 of the full area of the circle pi r squared

  • To calculate the area of a sector:

    • STEP 1
      Divide the angle by 360 to form a fraction

      • theta over 360

    • STEP 2
      Calculate the area of the full circle

      • pi r squared

    • STEP 3
      Multiply the fraction by the area

      • theta over 360 cross times pi r squared

Sector Area & Arc Length Formulae

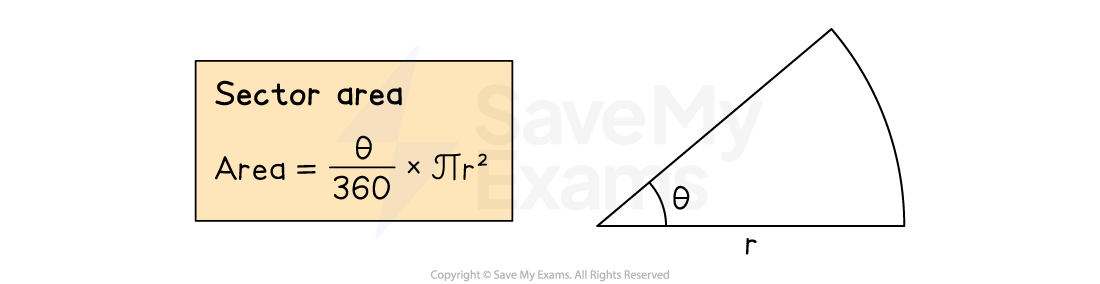
Worked Example

The diagram below shows a sector of a circle, centre straight C.

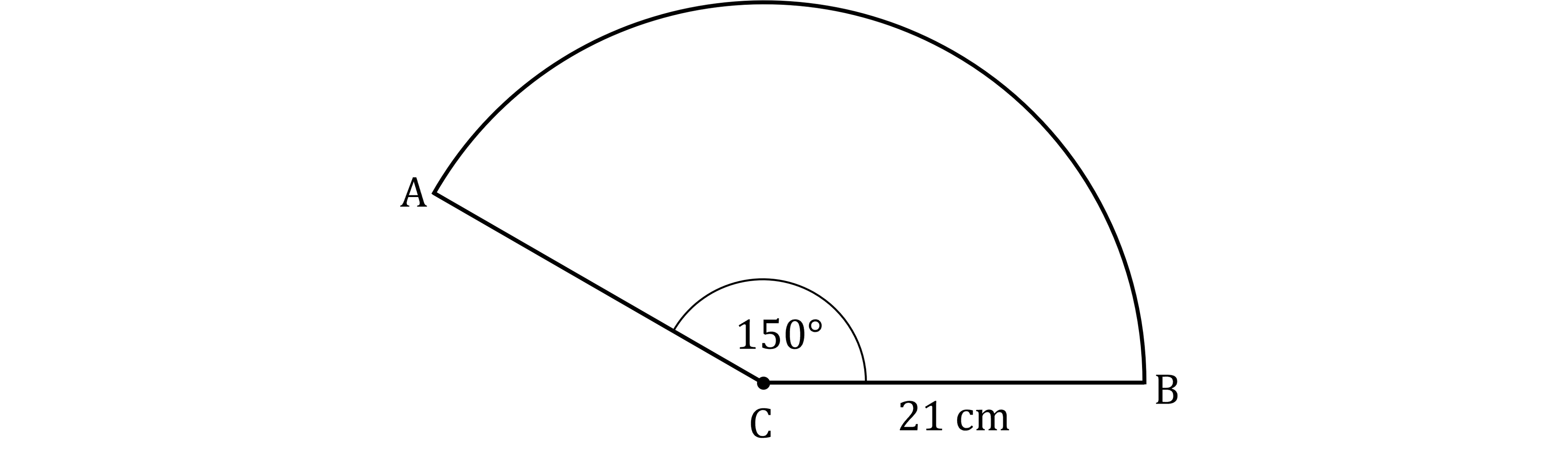
A circle sector with centre C, angle 150 degrees, and radius measuring 21 cm. Points A and B mark the ends of the sector's arc.

The radius of the circle is 21 centimetres and angle ACB is 150°.

Calculate the area of the sector.

Give your answer correct to one decimal place.

Answer:

Divide the angle by 360 to form a fraction

  • Here space theta equals 150 degree

theta over 360 equals 150 over 360

Use A equals pi r squared to find the area of the full circle

  • Here r equals 21

pi r squared equals pi cross times 21 squared

Multiply the fraction by the area

  • This is the same as substituting space theta equals 150 and r equals 21 into the formula sector space area equals theta over 360 cross times pi r squared

  • If you remember that formula you can skip right to this step!

 sector space area equals 150 over 360 cross times pi cross times 21 squared

Use your calculator to work out that value 

equals 577.267650...

Round your answer to 1 decimal place, as required

577.3 cm2 (1 d.p.)

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Multiplication & Division with FractionsNext:Problem Solving with Arcs & Sectors
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.