National 5MathsSQARevision NotesGeometric SkillsCircle GeometryProblem Solving with Arcs & Sectors

Problem Solving with Arcs & Sectors (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Problem solving with arcs & sectors

How do I solve more challenging questions involving arcs and sectors?

  • You will not always be given the radius r and angle at the centre theta and asked to find the arc length or sector area

    • Instead you may be given, say, the radius and the arc length

      • and need to find the angle at the centre

      • which may then be used to find the sector area

  • These sorts of questions can always be answered using the following process:

    • Start with the formula that includes the two values you know

      • Arc space length equals theta over 360 cross times 2 pi r space or space Sector space area equals theta over 360 cross times pi r squared

    • Substitute the values you know into the formula

    • Solve the resulting equation to find the missing value

  • Once you know the missing value, you can do anything else with it that the question requires

Examiner Tips and Tricks

It may be easier to keep any missing values you find as exact values in terms of pi.

  • This is especially true if you need to calculate something else using the missing value

  • You can also use your calculator's memory or the 'Ans' key to store the exact value

Worked Example

The diagram shows a sector of a circle, centre straight C.

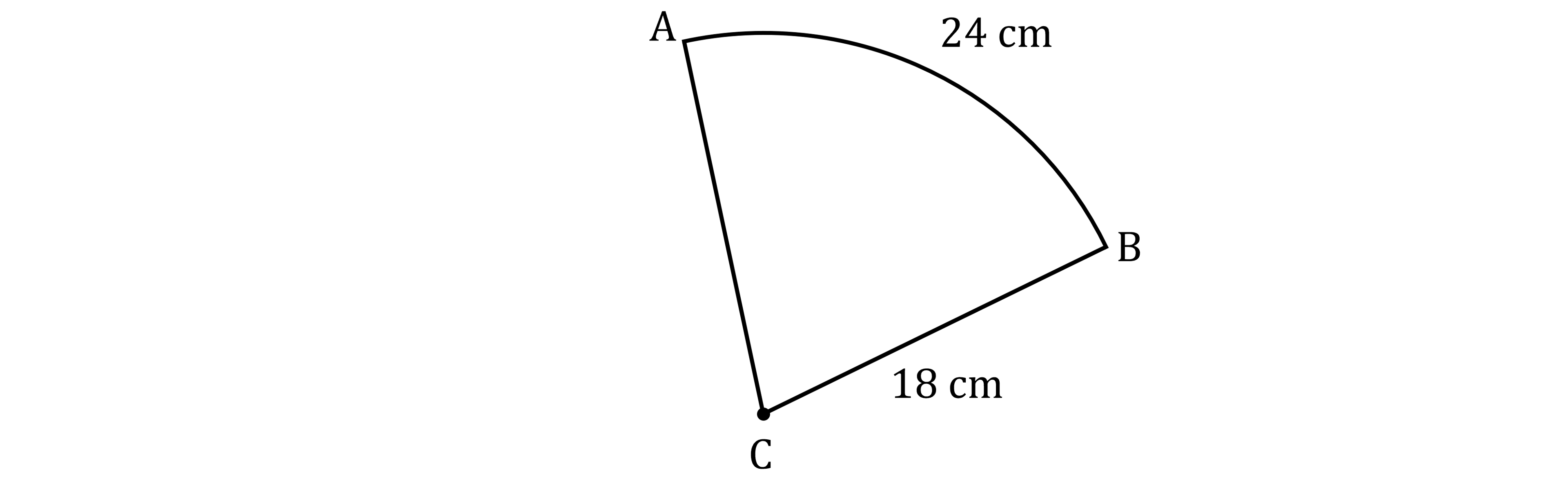
Diagram of sector ABC with curved side AB labelled 24 cm, and straight side BC labelled 18 cm.

The radius of the circle is 18 centimetres.

The length of arc AB is 24 centimetres.

Calculate the area of the sector.

Answer:

You know the arc length (24 cm) and the radius (18 cm)

  • Substitute those values into space Arc space length equals theta over 360 cross times 2 pi r space

24 equals theta over 360 cross times 2 pi cross times 18 space

Solve that equation to find the value of the angle at the centre, theta

24 equals theta over 360 cross times 36 pi space 24 equals theta cross times fraction numerator up diagonal strike 36 pi over denominator 10 up diagonal strike 360 end fraction 24 equals theta cross times pi over 10 240 equals theta cross times pi 240 over pi equals theta

240 over pi equals 76.394372... degree, but it is best here to keep theta as an exact value

  • The pi will cancel out in the next step!

Now you know the radius (18 cm) and the angle at the centre open parentheses fraction numerator 240 degree over denominator pi end fraction close parentheses

  • Substitute those into space Sector space area equals theta over 360 cross times pi r squared

table row cell space Sector space area end cell equals cell fraction numerator open parentheses 240 over pi close parentheses over denominator 360 end fraction cross times pi cross times 18 squared end cell row blank equals cell fraction numerator 2 up diagonal strike 240 over denominator 3 up diagonal strike 360 cross times pi end fraction cross times pi cross times 18 squared end cell row blank equals cell fraction numerator 2 over denominator 3 up diagonal strike pi end fraction cross times up diagonal strike pi cross times 18 squared end cell row blank equals cell 2 over 3 cross times 18 squared end cell row blank equals 216 end table

Remember to include the units with your final answer

216 cm2

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Arcs & SectorsNext:Sphere, Cone & Pyramid
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.