Circles (SQA National 5 Maths): Revision Note
Exam code: X847 75
Relationship between the centre, chord and perpendicular bisector
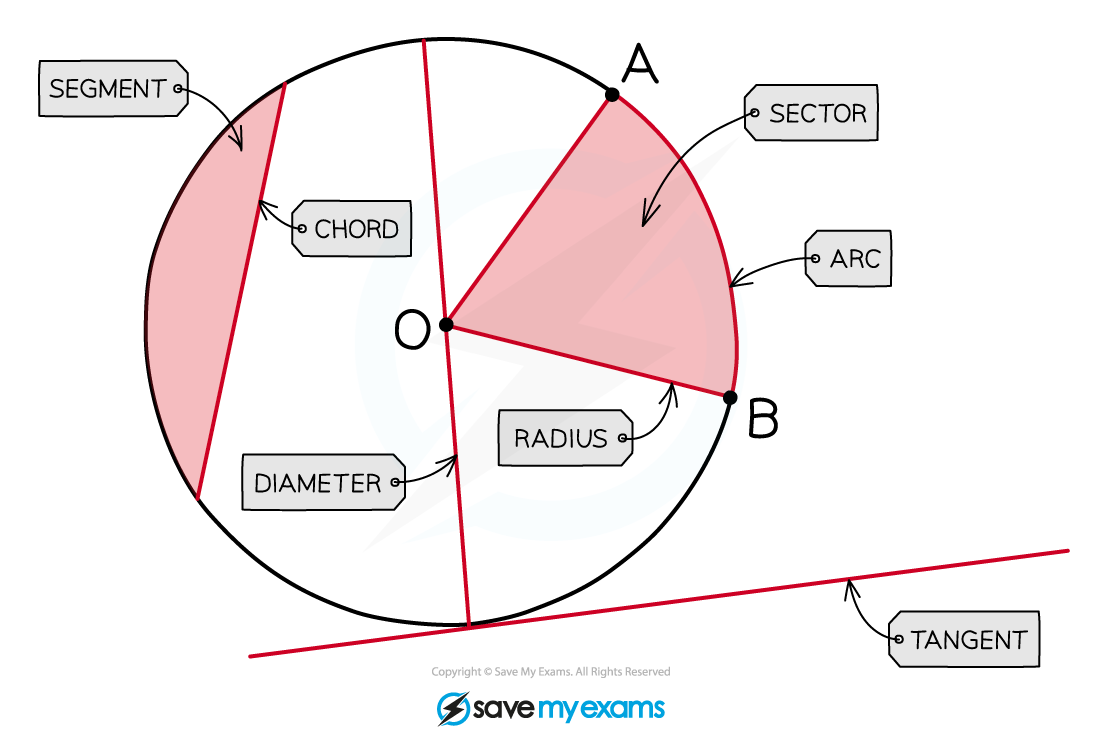
What terms related to circles do I need to know?
Circles have several specific terms that you need to be familiar with:
A circle's perimeter is called a circumference
Its line of symmetry is called a diameter
The line from the centre of the circle to its circumference is called a radius
The diameter is equal to 2 × the radius
A portion of the circumference is called an arc
A portion of the area, contained between two radii and an arc, is called a sector
A line between two points on the circumference is called a chord
The area formed between a chord and an arc is called a segment
A line which intersects the circumference at one point only, is called a tangent
The ratio
is equal to 𝝅 (3.14159...)
There are many properties relating to angles and other features of circles
These properties are sometimes known as circle theorems
You should be familiar with some of these from your National 4 Maths course
For example, the angle at the circumference in a semicircle is 90°
Or a tangent at a point on the circumference is perpendicular to a radius at that point
Circle Property: The perpendicular bisector of a chord passes through the centre
If a line through the centre (such as a radius or diameter) goes through the midpoint of chord
it will bisect (cut in half) that chord at right angles to it

To spot this circle property on a diagram
look for a radius and see if it intersects any chords
or look to see if you could draw a radius that bisects a chord
If you need to explain this property in an exam you could use either phrase below:
A radius bisects a chord at right angles
The perpendicular bisector of a chord passes through the centre
Examiner Tips and Tricks
In exam questions it is often necessary to combine this circle property with Pythagoras' theorem to find a missing length.
Worked Example
A plastic game piece has a circular cross-section with a horizontal bottom.
A diagram of the cross-section is shown below.
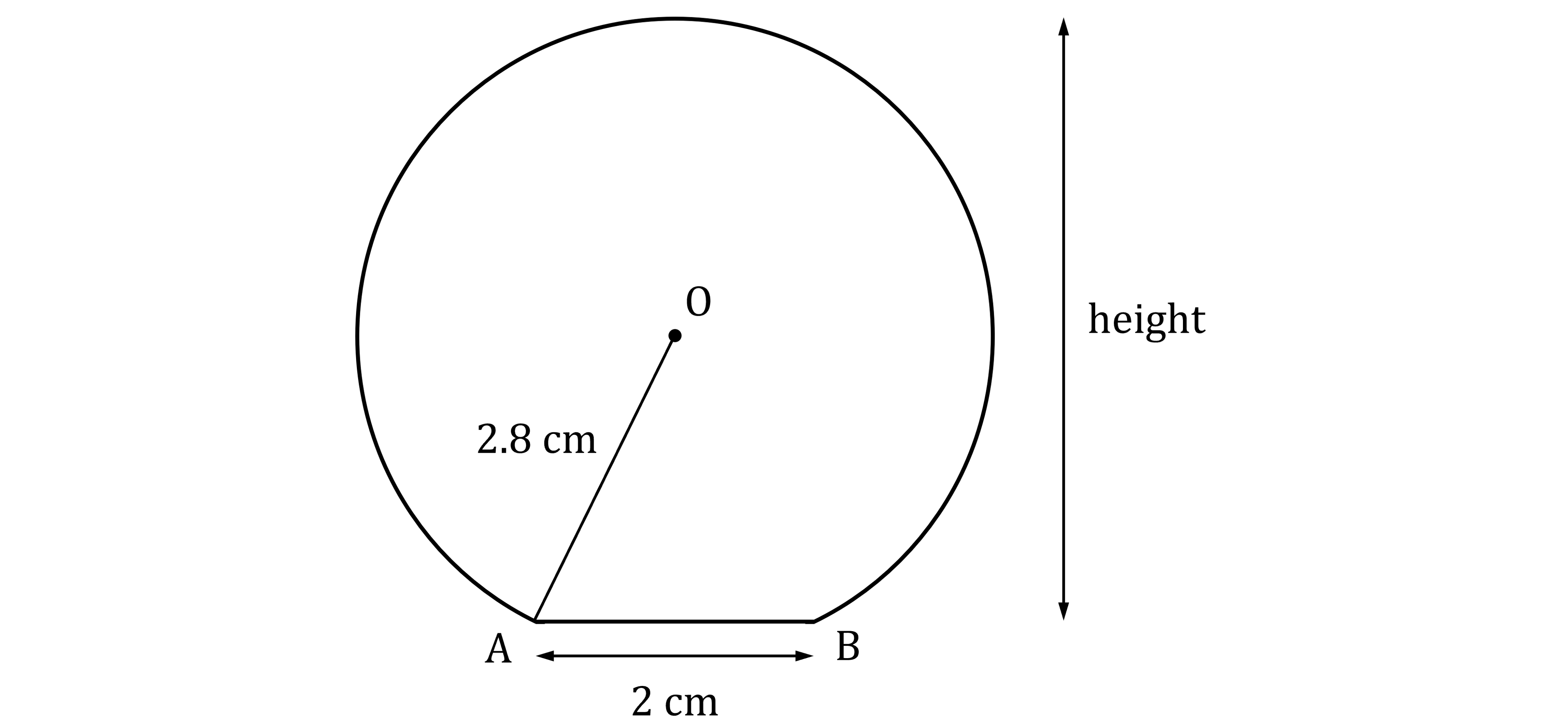
The centre of the circle is O.
Chord AB is 2 centimetres.
The radius OA is 2.8 centimetres.
Calculate the height of the game piece.
Give your answer correct to 2 significant figures.
Answer:
Draw a line through the centre perpendicular to AB
By the property "the perpendicular bisector of a chord passes through the centre", this line will divide AB in half
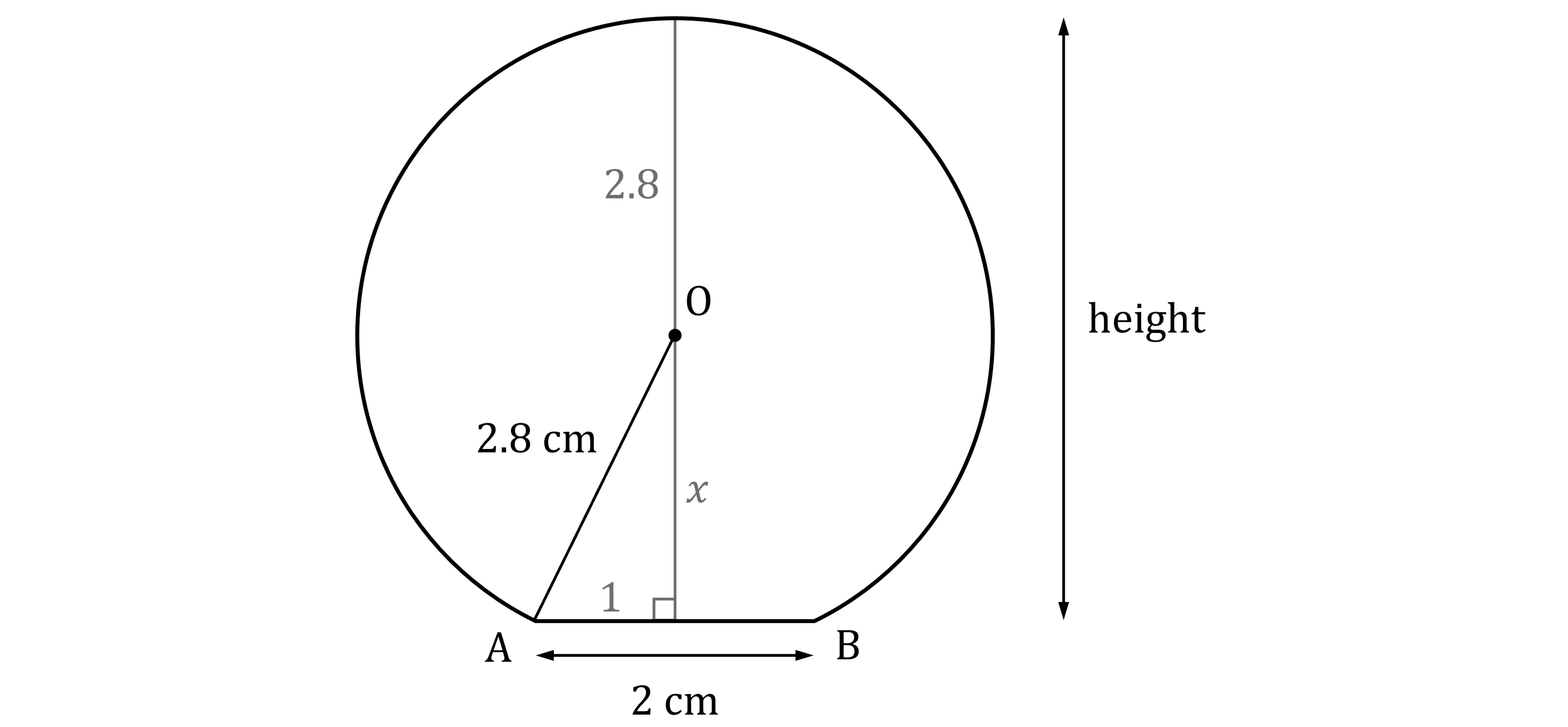
The height you are looking for is equal to
But is one of the sides in a right-angled triangle
So you can use Pythagoras' theorem to find the value of
Therefore the height is equal to
Round to 2 significant figures, as required
5.4 cm (2 s.f.)

Unlock more, it's free!
Was this revision note helpful?
