National 5MathsSQARevision NotesGeometric SkillsPythagoras' TheoremConverse of Pythagoras' Theorem

Converse of Pythagoras' Theorem (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Using the converse of Pythagoras' theorem

What is Pythagoras' theorem?

  • You should be familiar with Pythagoras' theorem from your National 4 Maths course

    • The theorem gives a formula that links the lengths of the three sides of a right-angled triangle

  • Pythagoras' theorem states that  a squared plus b squared equals c squared

    • c  is the length of the hypotenuse

      • The hypotenuse is the longest side, and is always opposite the right angle

    • a  and  b  are the lengths of the two shorter sides 

      • It does not matter which is labelled a and which is labelled b

A right-angled triangle with the sides labelled a, b and c

What is the converse of Pythagoras' theorem?

  • If you know that a triangle is right-angled, then you can use Pythagoras' theorem to find a missing side if you know the other two sides

    • If the triangle is right-angled, then space a squared plus b squared equals c squared

  • The converse of Pythagoras' theorem can be used to show whether or not a triangle is right-angled if you know the three side lengths

    • If space a squared plus b squared equals c squared, then the triangle is right-angled

    • If space a squared plus b squared not equal to c squared, then the triangle is not right-angled

How do I use the converse of Pythagoras' theorem to determine whether or not a triangle is right-angled?

  • For example: A triangle has side lengths of 5 cm, 12 cm and 14 cm. Determine whether or not the triangle is right-angled

    • Work out the values of a squared plus b squared and c squared

      • Make sure that you use the longest side as c

        • It doesn't matter which of the other two sides is a, and which is b

      • a squared plus b squared equals 5 squared plus 12 squared equals 25 plus 144 equals 169

      • c squared equals 14 squared equals 196

    • If the two values are equal, then the triangle is right-angled

    • If the two values are not equal, then the triangle is not right-angled

      • Here 169 not equal to 196

      • Therefore the triangle is not right-angled

Examiner Tips and Tricks

Students have tended to lose a lot of marks on these questions in past papers.

In particular, do not start by substituting the three sides into space a squared plus b squared equals c squared.

  • So in the example above, do not write 5 squared plus 12 squared equals 14 squared

  • You will lose a mark for doing this, even if everything else is correct

Examiner Tips and Tricks

In exams, converse Pythagoras questions have tended to appear in the context of 'real-life' scenarios.

  • Look out for questions where you are asked to determine whether two things are perpendicular

  • Be sure to answer in the context of the question

Worked Example

A ladder is leaned against a wall built on horizontal ground as shown in the diagram.

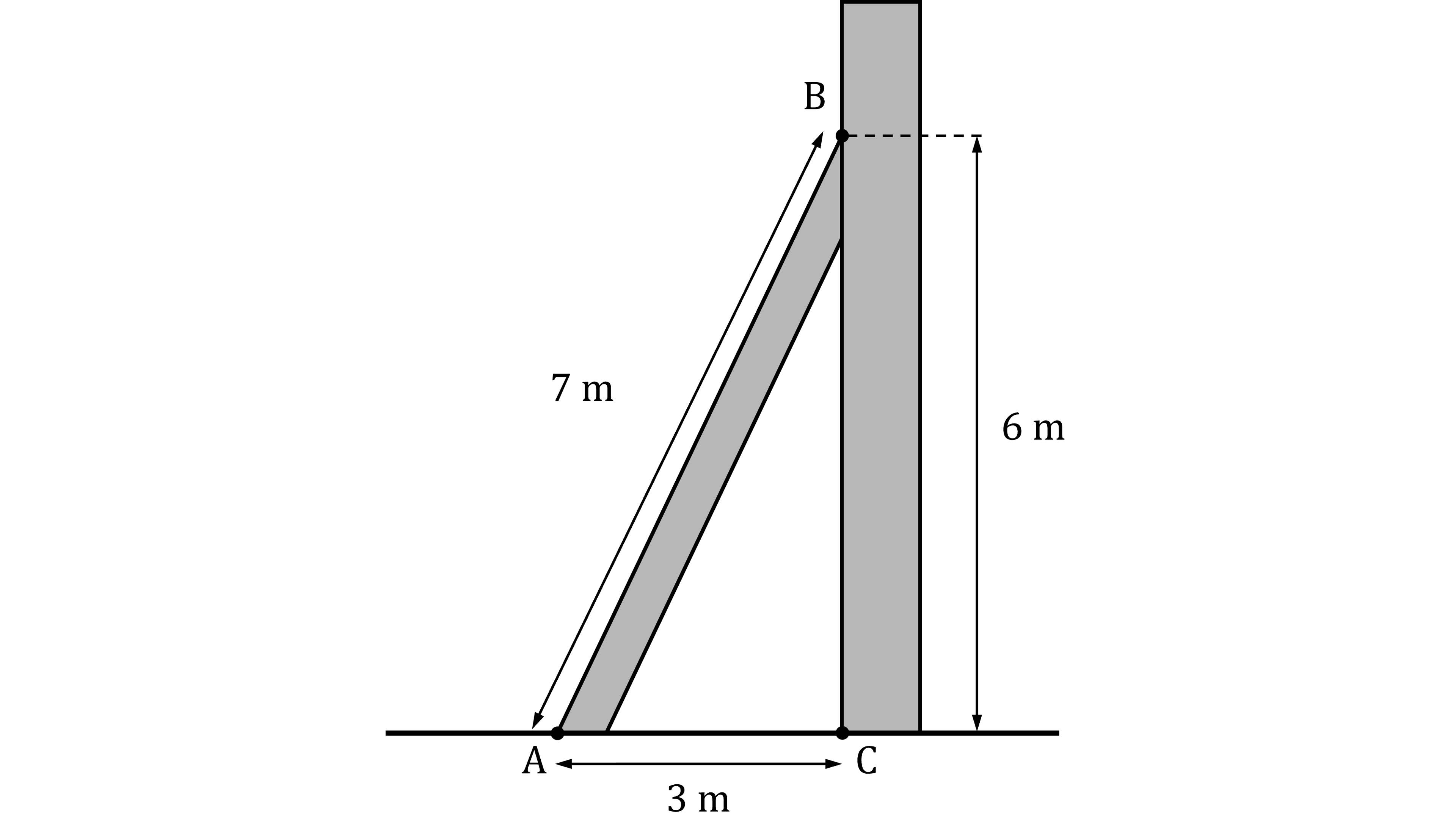
Diagram of a right triangle with points A, B, C. AC is a horizontal line and labelled 3m, AB is labelled 7m, and BC is labelled 6m. A shaded rectangle is adjacent to BC, and a shaded trapezoid is adjacent to AB.

The edge of the ladder, AB, is 7 metres long.

C is at the foot of the wall.

A is 3 metres from C.

B is 6 metres from C.

Determine whether the wall is perpendicular to the ground.

Justify your answer.

Answer:

You need to determine whether or not angle ACB is a right angle

  • If it is, then the wall is perpendicular to the ground

  • If it is not, then the wall is not perpendicular to the ground

Use the converse of Pythagoras' theorem

  • Let c equals 7, because the 7 m side is the longest side of the triangle

  • a and b will be 3 and 6 (which is which isn't important)

Calculate a squared plus b squared

table row cell a squared plus b squared end cell equals cell 3 squared plus 6 squared end cell row blank equals cell 9 plus 36 end cell row blank equals 45 end table

Calculate c squared

c squared equals 7 squared equals 49

State that those are not equal

45 not equal to 49

Because they are not equal, the triangle is not a right-angled triangle

  • This means angle ACB is not a right angle

  • Which means the wall isn't perpendicular to the ground

Write your conclusion, giving a justification and answering in the context of the question

The wall is not perpendicular to the ground, because angle ACB is not a right angle

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Composite SolidsNext:Pythagoras' Theorem in 3D
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.