National 5MathsSQARevision NotesGeometric SkillsSimilaritySimilar Areas & Volumes

Similar Areas & Volumes (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Similar areas & volumes

What are similar shapes?

  • Two shapes are mathematically similar if they have the same shape and their corresponding sides are in proportion

    • One shape is an enlargement of the other

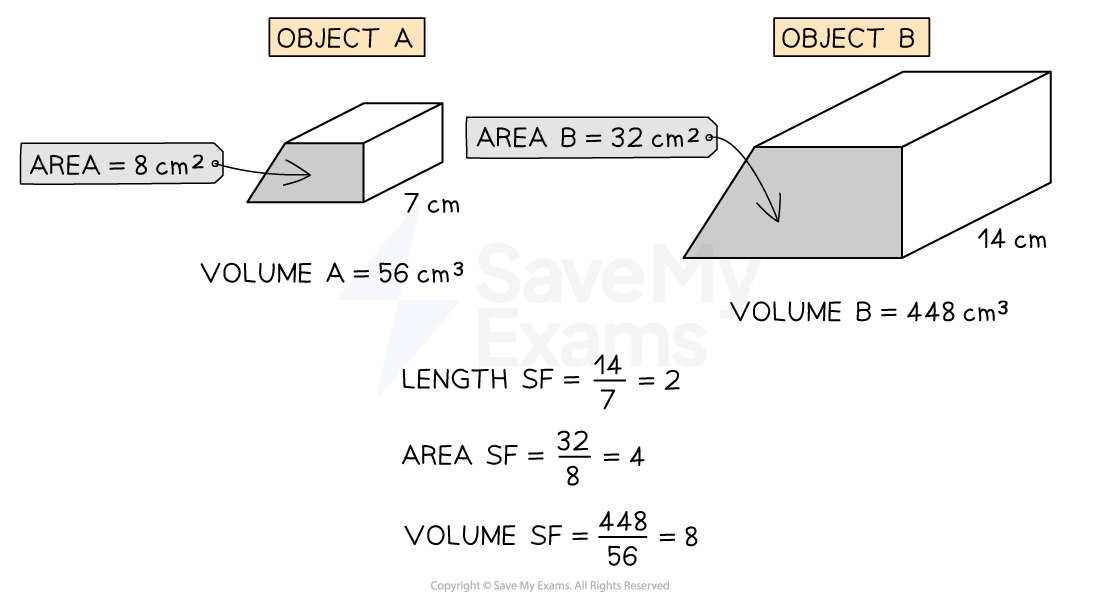
How do I find the length, area or volume scale factors of similar shapes?

  • The scale factor (SF) for a given quantity (length, area or volume), can be found by dividing the quantity on one shape by the quantity on the other shape

    • scale space factor equals fraction numerator quantity space on space one space shape over denominator corresponding space quantity space on space the space other space shape end fraction

Two objects, A and B. Object A has a depth of 7 cm, a front surface area of 8 cm² and a volume of 56 cm³. Object B has a depth of 14 cm, a front surface area of 32 cm² and a volume of 448 cm³. Length SF = 2, area SF = 4, volume SF = 8.

  • An object could be made either bigger or smaller by a scale factor

    • When k > 1, the object is getting bigger

      • This is also true for k2 > 1 and k3 > 1

    • When 0 < k < 1, the object is getting smaller

      • This is also true for 0< k2 < 1 and 0 < k3 < 1

What is the connection between the scale factors for lengths, areas and volumes of similar shapes?

  • In mathematically similar shapes

    • the length, area and volume scale factors can be written as powers with the same base number

  • If the length scale factor is k then

    • The area scale factor is k2

    • The volume scale factor is k3

  • If you know one scale factor, you can find the other scale factors

    • If you have the length scale factor

      • Area space scale space factor equals open parentheses Length space scale space factor close parentheses squared

      • Volume space scale space factor equals open parentheses Length space scale space factor close parentheses cubed

    • If you have the area scale factor

      • Length space scale space factor equals square root of Area space scale space factor end root

      • Volume space scale space factor equals open parentheses square root of Area space scale space factor end root close parentheses cubed

    • If you have the volume scale factor

      • Length space scale space factor equals cube root of Volume space scale space factor end root

      • Volume space scale space factor equals open parentheses cube root of Volume space scale space factor end root close parentheses squared

How do I find missing lengths, areas and volumes for similar shapes?

  • STEP 1
    Identify the equivalent known quantities

    • Recognise if the quantities are lengths, areas or volumes

  • STEP 2
    Find the scale factor from two known lengths, areas or volumes

    • scale space factor equals fraction numerator second space quantity over denominator first space quantity end fraction

  • STEP 3
    Use the scale factor you have found to find other required scale factor(s)

    • Length space scale space factor equals k

    • Area space scale space factor equals k squared

    • Volume space scale space factor equals k cubed

  • STEP 4
    Multiply or divide by relevant scale factor to find the missing quantity

    • Think about whether the quantity should be bigger or smaller than the given quantity

Examiner Tips and Tricks

Take extra care not to mix up which shape is which when you have started carrying out the calculations.

  • It can help to label the shapes and write an equation

Worked Example

Solid A and solid B are mathematically similar. 

The height of solid A is 10 cm.
The height of solid B is 15 cm.

The surface area of solid A is 80 cm2.
The volume of solid A is 32 cm3.

(a) Find the surface area of solid B.

(b) Find the volume of solid B.

Answer:

Part (a)

Divide the height of B by the height of A to find the length scale factor k

  • k equals fraction numerator height space of space B over denominator height space of space A end fraction

table row k equals cell 15 over 10 equals 3 over 2 end cell end table

Square that to find the area scale factor, k2

k squared equals open parentheses 3 over 2 close parentheses squared equals 9 over 4

B has a larger height than A, so it will also have a larger surface area

  • Multiply the surface area of A by k2 to find the surface area of B

table row cell 80 cross times 9 over 4 end cell equals 180 end table

Don't forget to include units in your final answer

180 cm2

Part (b)

You already know the length scale factor, k, from part (a)

Cube that to find the volume scale factor, k3

k cubed equals open parentheses 3 over 2 close parentheses cubed equals 27 over 8

B has a larger height than A, so it will also have a larger volume

  • Multiply the volume of A by k3 to find the volume of B

table row cell 32 cross times 27 over 8 end cell equals 108 end table

Don't forget to include units in your final answer

108 cm3

Using scale factors to test similarity

How do I use scale factors to show that two shapes are not similar?

  • If two shapes are mathematically similar then the following relationships must be true

    • Length space scale space factor equals k

    • Area space scale space factor equals k squared

    • Volume space scale space factor equals k cubed

      • If you know one of the scale factors, then the other two are determined automatically

  • If those relationships are not true then the shapes are not similar

    • You can use this in the exam to show that two shapes are not similar

    • E.g. if the length scale factor for two shapes is 4 and the area scale factor is 15

      • 4 squared equals 16, which is not equal to 15

      • The length factor squared is not equal to the area scale factor

      • So the two shapes are not mathematically similar

Examiner Tips and Tricks

Note that you cannot use this test to prove that two shapes definitely are similar. You can only use it to show that two shapes are not similar.

Worked Example

A sports stadium sells soft drinks in two different sized cups.

The small cup has a height of 12 centimetres and a volume of 330 cubic centimetres.

The large cup has a height of 13.5 centimetres and a volume of 440 cubic centimetres.

Show that the two cups are not mathematically similar.

Answer:

Divide the height of the large cup by the height of the small cup to find the length scale factor

table row cell length space scale space factor end cell equals cell fraction numerator 13.5 over denominator 12 end fraction equals 9 over 8 end cell end table

Cube that to find what the volume scale factor would be, if the cups were mathematically similar

open parentheses 9 over 8 close parentheses cubed equals 729 over 512 equals 1.423828...

Divide the volume of the large cup by the volume of the small cup to find the actual length scale factor

table row cell volume space scale space factor end cell equals cell 440 over 330 equals 4 over 3 equals 1.333333... end cell end table

Those are not equal, so the cups are not mathematically similar

  • Be sure to give your reason

The volume scale factor is not equal to the length scale factor cubed, so the cups are not mathematically similar

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:CirclesNext:Component Vectors in 2D and 3D
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.