National 5MathsSQARevision NotesGeometric SkillsVectorsGeometry of Vector Addition & Subtraction

Geometry of Vector Addition & Subtraction (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Adding & subtracting with directed line segments

How can I represent a vector visually?

  • A vector has both a size (magnitude) and a direction

    • You can represent this using a directed line segment

    • You need to draw a line to show the size of the vector

    • You also need to draw an arrowhead to show the direction of the vector

      • The arrowhead can be drawn at the end of the line, or in the middle of the line

Magnitude and direction of a vector

 

  • A vector written as AB with rightwards arrow on top will have points straight A and straight B as its endpoints

    • Here the arrow will point towards B

    • Vector stack B A with rightwards arrow on top will have the same length but will point towards A

Vector between two points

How do I draw a vector on a grid?

  • You can draw a vector anywhere on a grid

    • Just make sure it has the correct length and the correct direction

  • To draw the vector bold a equals open parentheses table row 3 row 4 end table close parentheses

    • Pick a point on the grid and draw a dot there

    • Count 3 units to the right and 4 units up and draw another dot

    • Draw a line between the two dots

    • Put an arrow on the line pointing toward the second dot

  • Look out for negatives and zeroes

    • bold b equals open parentheses table row 2 row cell negative 4 end cell end table close parentheses  goes 2 to the right and 4 down

    • bold c equals open parentheses table row 2 row 0 end table close parentheses goes 2 to the right but does not go up or down

Vectors on a grid

What happens when I multiply a vector by a scalar?

  • When you multiply a vector by a positive scalar:

    • The direction stays the same

    • The length of the vector is multiplied by the scalar

  • For example, bold a equals open parentheses table row 4 row cell negative 2 end cell end table close parentheses

    • 2 bold a equals open parentheses table row 8 row cell negative 4 end cell end table close parentheses will have the same direction but double the length

    • 1 half bold a equals open parentheses table row 2 row cell negative 1 end cell end table close parentheses will have the same direction but half the length

Multiplying vectors by a scalar

  • When you multiply a vector by a negative scalar:

    • The direction is reversed

    • The length of the vector is multiplied by the number after the negative sign

  • For example, bold a equals open parentheses table row 4 row cell negative 2 end cell end table close parentheses

    • negative bold a equals open parentheses table row cell negative 4 end cell row 2 end table close parentheses will be in the opposite direction and its length will be the same

    • negative 2 bold a equals open parentheses table row cell negative 8 end cell row 4 end table close parentheses will be in the opposite direction and its length will be doubled

Multiplying a vector by a negative scalar

How do I represent addition or subtraction of vectors using directed line segments?

  • To draw the vector bold a plus bold b

    • Draw the vector bold a

    • Draw the vector bold b starting at the endpoint of bold a

    • Vector bold a plus bold b is the line that starts at the start of bold a and ends at the end of bold b

  • To draw the vector bold a minus bold b 

    • Draw the vector bold a

    • Draw the vector negative bold b  starting at the endpoint of bold a

    • Vector bold a bold minus bold b is the line that starts at the start of bold a  and ends at the end of negative bold b

Adding and subtracting vectors

Worked Example

Vectors bold r and bold s have components bold r equals open parentheses table row 4 row 3 end table close parentheses and bold q equals open parentheses table row 2 row cell negative 5 end cell end table close parentheses.

Draw the resultant vector bold r plus bold s on the grid.

A blank 10x10 grid with thin black lines on a white background.

Answer:

Method 1

Start by drawing vector bold r

  • It can start anywhere (as long as everything in the final diagram fits!)

  • From where it starts, it should go 4 squares to the right and 3 squares up

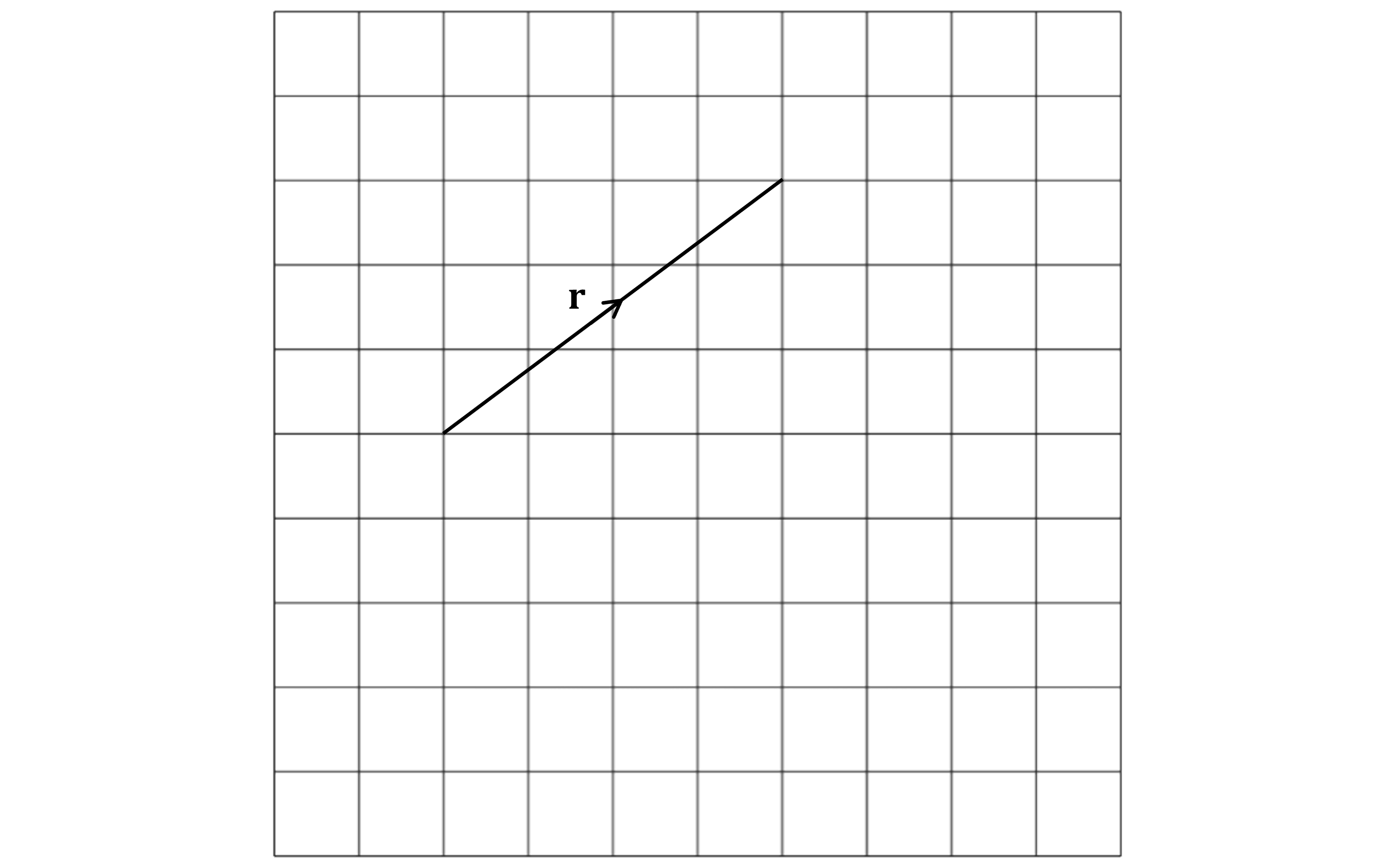
Vector labelled "r" on a grid pointing from bottom left to top right, going 4 to the right and 3 up.

Next draw vector bold s

  • To indicate bold r plus bold s, it should start where vector bold r ends

  • Then it should go 2 squares to the right and 5 squares down

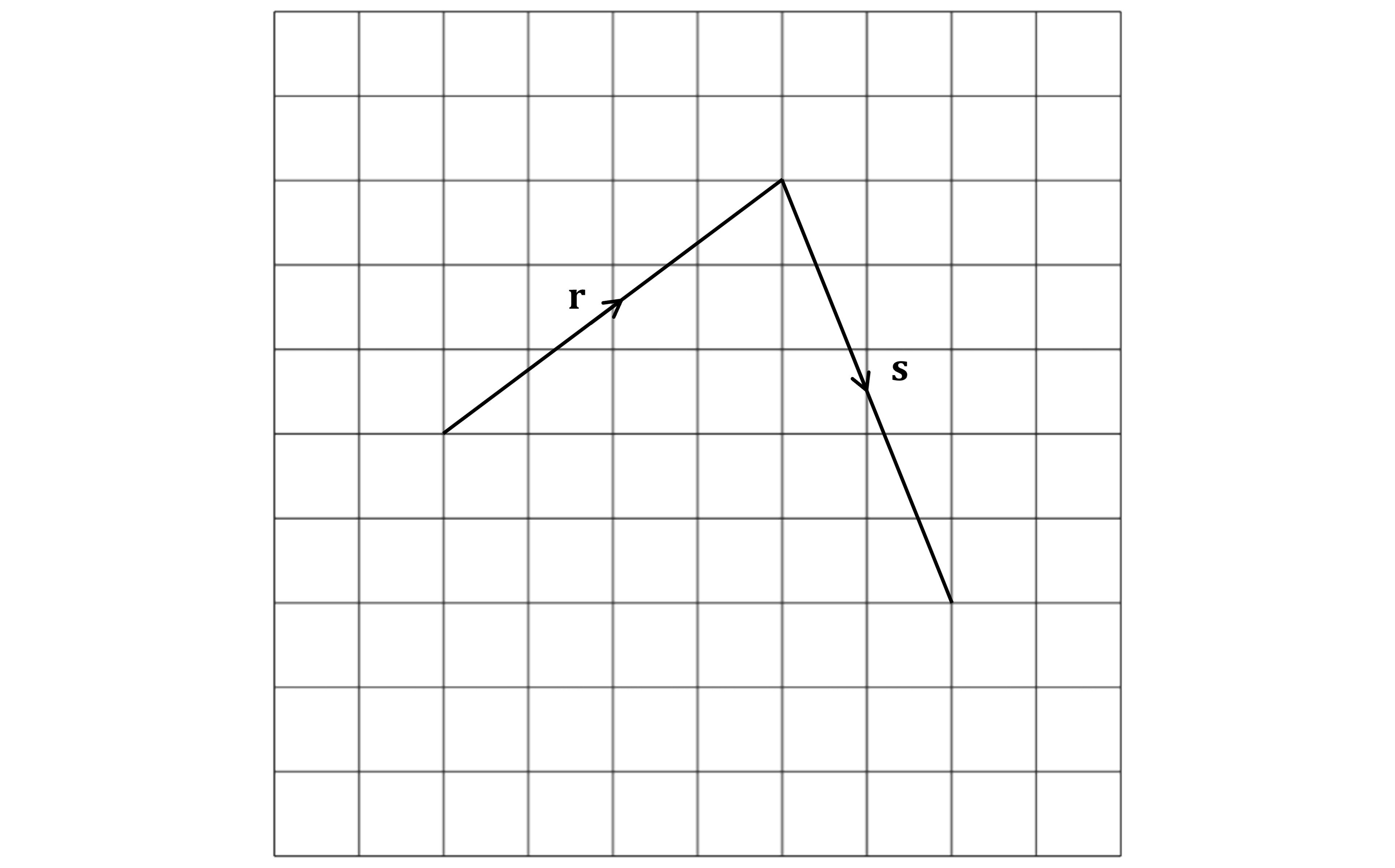
Grid with two vectors, r and s, with tail of s following on from head of r. Vector r goes 4 to the right and 3 up; vector s goes 2 to the right and 5 down.

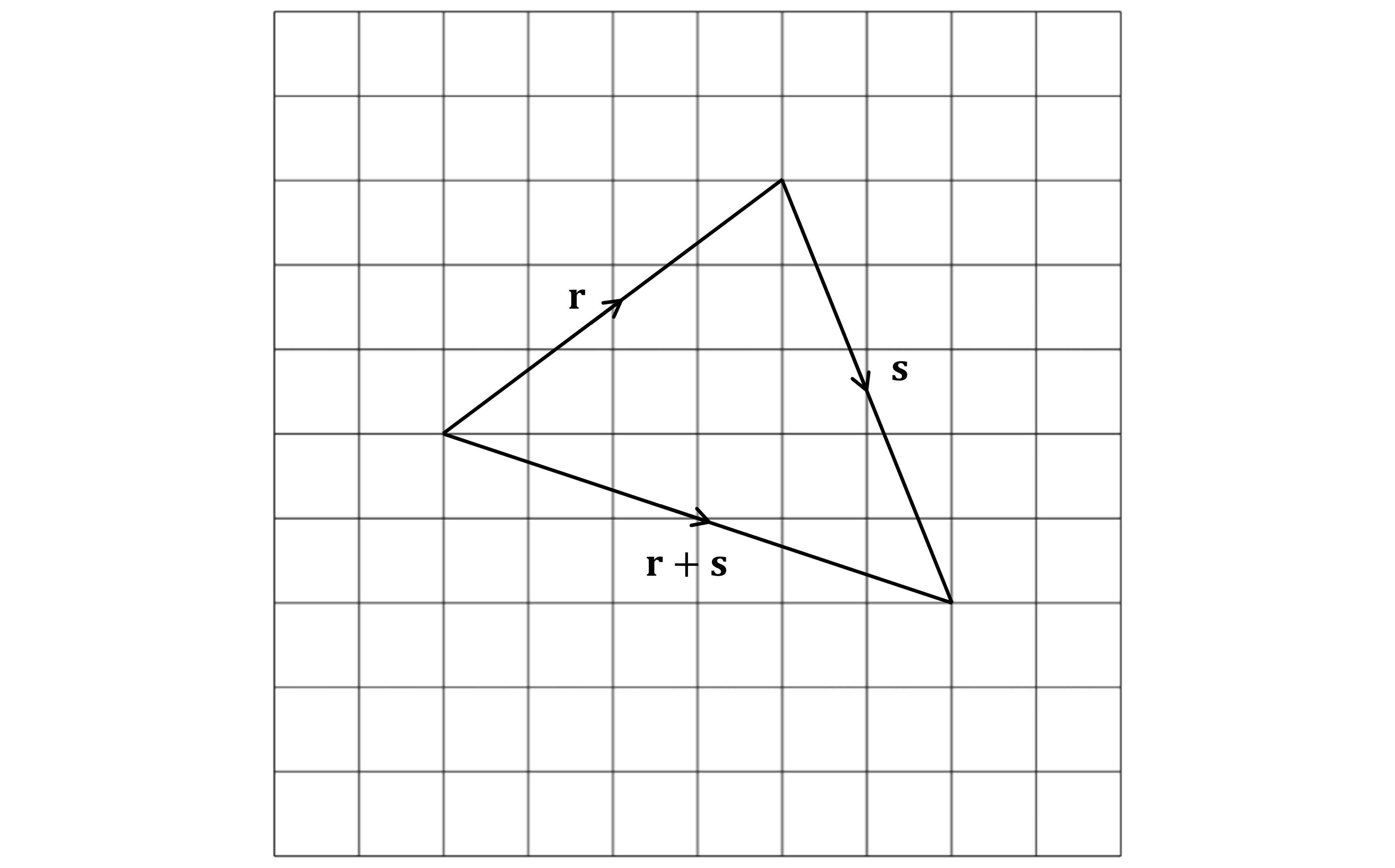
Finally draw the vector bold r plus bold s

  • It should start at the beginning of bold r and go to the end of bold s

  • Be sure to include an arrowhead pointing in the right direction

Grid with three vectors, labelled r, s, and r+s, forming a triangle. Vector r goes 4 to the right and 3 up. The tail of vector s starts at the head of vector r, and vector s goes 2 to the right and 5 down. Vector r+s goes from the tail of vector r to the head of vector s, and vector r+s goes 6 to the right and 2 down.

Method 2

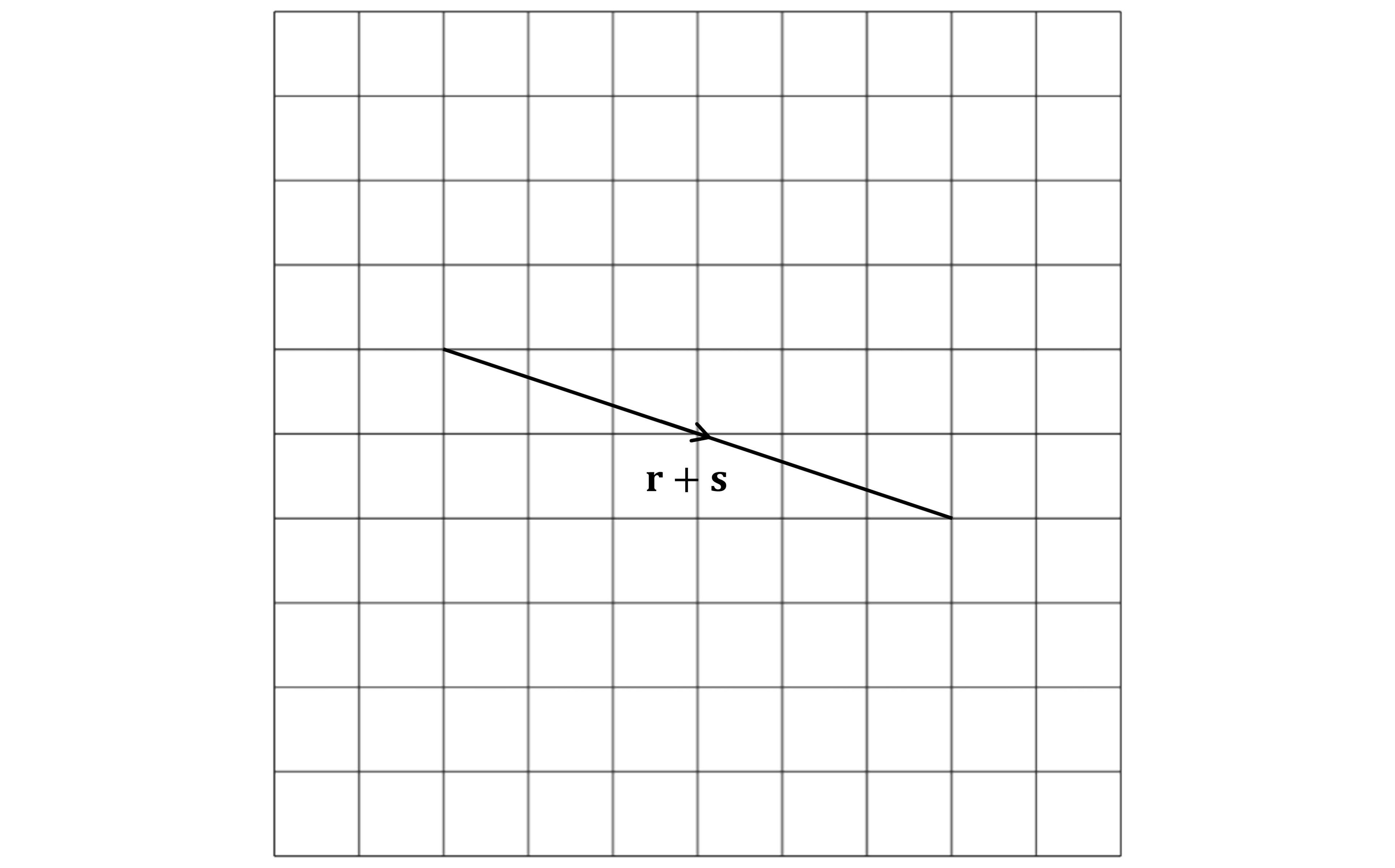
Calculate bold r plus bold s numerically

table row cell bold r plus bold s end cell equals cell open parentheses table row 4 row 3 end table close parentheses plus open parentheses table row 2 row cell negative 5 end cell end table close parentheses end cell row blank equals cell open parentheses table row cell 4 plus 2 end cell row cell 3 plus open parentheses negative 5 close parentheses end cell end table close parentheses end cell row blank equals cell open parentheses table row cell 4 plus 2 end cell row cell 3 minus 5 end cell end table close parentheses end cell row blank equals cell open parentheses table row 6 row cell negative 2 end cell end table close parentheses end cell end table

Draw and label this vector on the grid

  • It can start anywhere (as long as it fits!)

  • From where it starts, it should go 6 squares to the right and 2 square down

  • Be sure to include an arrowhead showing which way the vector points

Grid with a vector pointing diagonally right and down and labelled "r + s". The vector goes 6 squares right, and 2 squares down.

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Magnitude of a VectorNext:Vector Pathways
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.