National 5MathsSQARevision NotesGeometric SkillsVectorsMagnitude of a Vector

Magnitude of a Vector (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

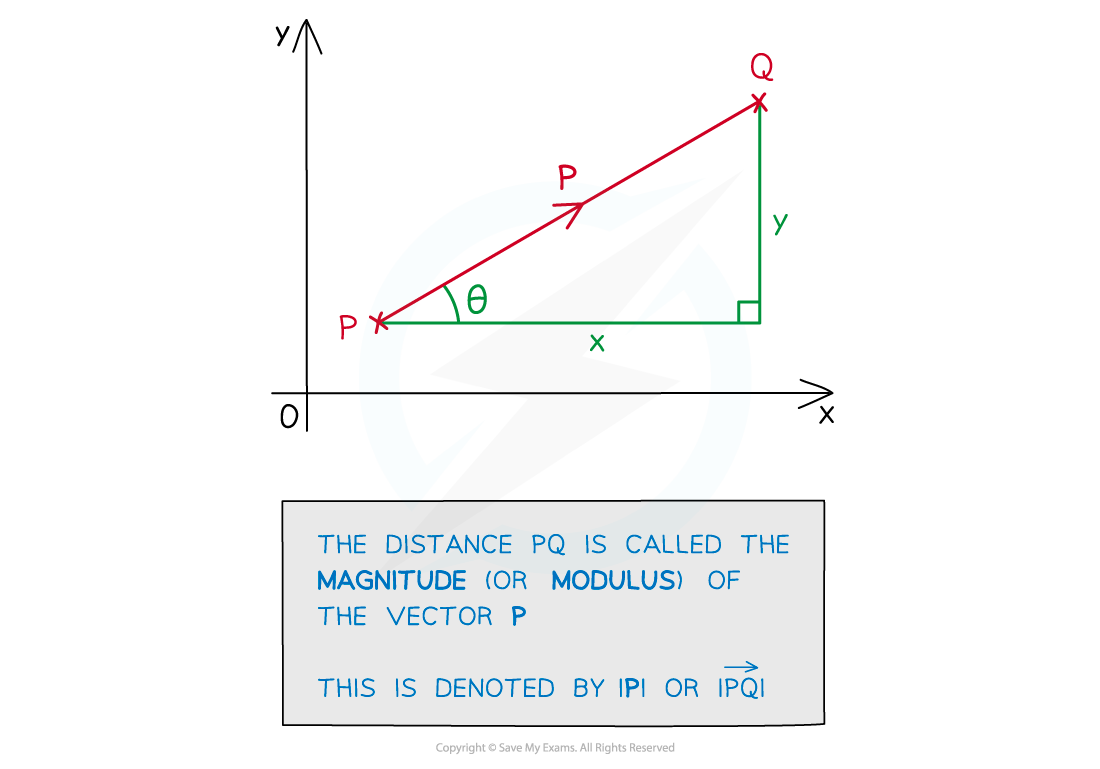
Calculating the magnitude of a vector

What is the magnitude of a vector?

  • The magnitude of a vector is its length

    • It is also called the modulus

    • This is always a positive value

    • The direction of the vector is irrelevant

  • The magnitude of vector stack A B with italic rightwards arrow on top is written open vertical bar stack A B with rightwards arrow on top close vertical bar

    • The magnitude of vector a is written |a|

  • In real world contexts, the magnitude of a vector can represent different quantities

    • For a velocity vector, its magnitude would be speed

    • For a force vector, its magnitude would be the strength of the force (in newtons)

How do I find the magnitude of a two-dimensional vector?

  • For a 2D vector in component form, the magnitude is the hypotenuse of a right-angled triangle

    • Use Pythagoras' theorem to find the magnitude

    • The magnitude of bold a equals open parentheses table row x row y end table close parentheses is

      • open vertical bar bold a close vertical bar equals square root of x to the power of 2 space end exponent plus blank y squared end root

Diagram showing a vector P with horizontal component x and vertical component y. The magnitude of the vector is |P|.

Examiner Tips and Tricks

If there is no diagram, sketch one!

  • You can sketch a vector and use it to form a right-angled triangle

How do I find the magnitude of a three-dimensional vector?

  • For a 3D vector in component form, the magnitude can be found using the following formula

    • The magnitude of bold a equals open parentheses table row x row y row z end table close parentheses is

      • open vertical bar bold a close vertical bar equals square root of x to the power of 2 space end exponent plus blank y squared plus z squared end root

  • This is formula is related to Pythagoras' Theorem in 3D

Worked Example

Consider two points A open parentheses negative 3 comma space 5 close parentheses and B open parentheses 7 comma space 1 close parentheses.

(a) Write down the vector stack A B with rightwards arrow on top in component form.

(b) Find the modulus of vector stack A B with rightwards arrow on top.

Answer:

Part (a)

Find the horizontal and vertical distances between the two points

  • You can do this by subtracting the x and y components of A from B

stack A B with rightwards arrow on top equals open parentheses table row cell 7 minus negative 3 end cell row cell 1 minus 5 end cell end table close parentheses

stack A B with italic rightwards arrow on top equals stretchy left parenthesis table row 10 row cell negative 4 end cell end table stretchy right parenthesis

Part (b)

Sketching a diagram of the vector stack A B with rightwards arrow on top can help

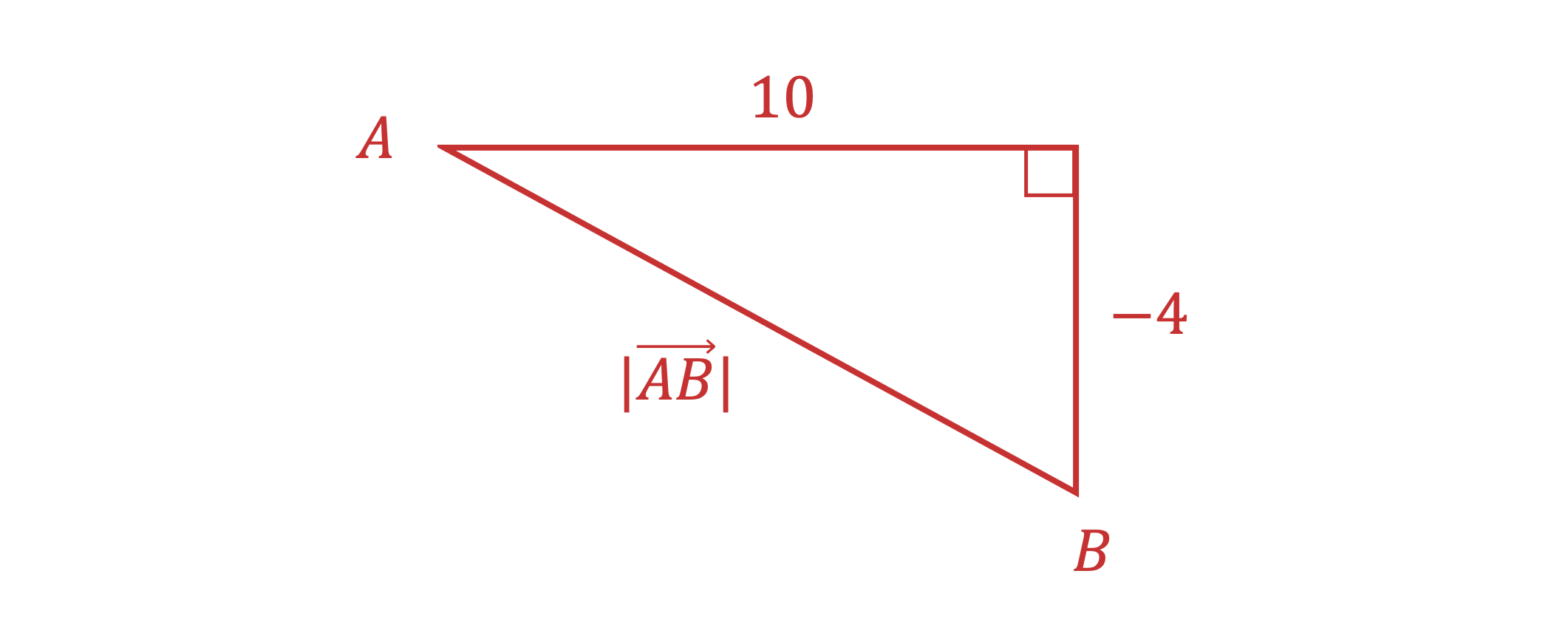
Right-angled triangle formed from points A and B. The horizontal distance is 10, the vertical distance is 4 and the hypotenuse is the magnitude of the vector from A to B.

Apply Pythagoras' theorem to the x and y components of stack A B with rightwards arrow on top

table row cell open vertical bar stack A B with rightwards arrow on top close vertical bar end cell equals cell square root of 10 squared plus open parentheses negative 4 close parentheses squared end root end cell row blank equals cell square root of 100 plus 16 end root end cell row blank equals cell square root of 116 end cell end table

Error converting from MathML to accessible text.

Worked Example

Find open vertical bar bold r close vertical bar, the magnitude of vector bold r equals open parentheses table row cell negative 36 end cell row 8 row 24 end table close parentheses.

Answer:

Use the formula open vertical bar bold a close vertical bar equals blank square root of x to the power of 2 space end exponent plus blank y squared plus z squared end root, where bold a equals blank open parentheses table row x row y row z end table close parentheses

table row cell open vertical bar bold r close vertical bar end cell equals cell square root of open parentheses negative 36 close parentheses to the power of 2 space end exponent plus blank 8 squared plus 24 squared end root end cell end table

Use your calculator to work that out

table row cell open vertical bar bold r close vertical bar end cell equals 44 end table

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Vector ArithmeticNext:Geometry of Vector Addition & Subtraction
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.