National 5MathsSQARevision NotesGeometric SkillsVectorsWorking with 3D coordinates

Working with 3D coordinates (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Determining coordinates of points on 3D diagrams

How do I determine missing coordinates of points on 3D diagrams?

  • An exam question may ask you to find missing coordinates of points on a 3D diagram

    • Usually these will be vertices or other points on the surface of a regular solid

  • You need to be familiar with the properties of regular solids

    • For example spheres, cones and pyramids

    • You should also be familiar with cubes, cuboids, prisms and cylinders from your National 4 Maths course

  • In particular look for faces of the solid that are parallel to each other and have the same size

    • For example the two 'end faces' of a prism

      • These both have the same shape and size (which is the cross-section of the prism)

      • And they are at a distance from each other equal to the length of the prism

  • You may also need to use the properties of triangles and quadrilaterals to work out some of the coordinates

Worked Example

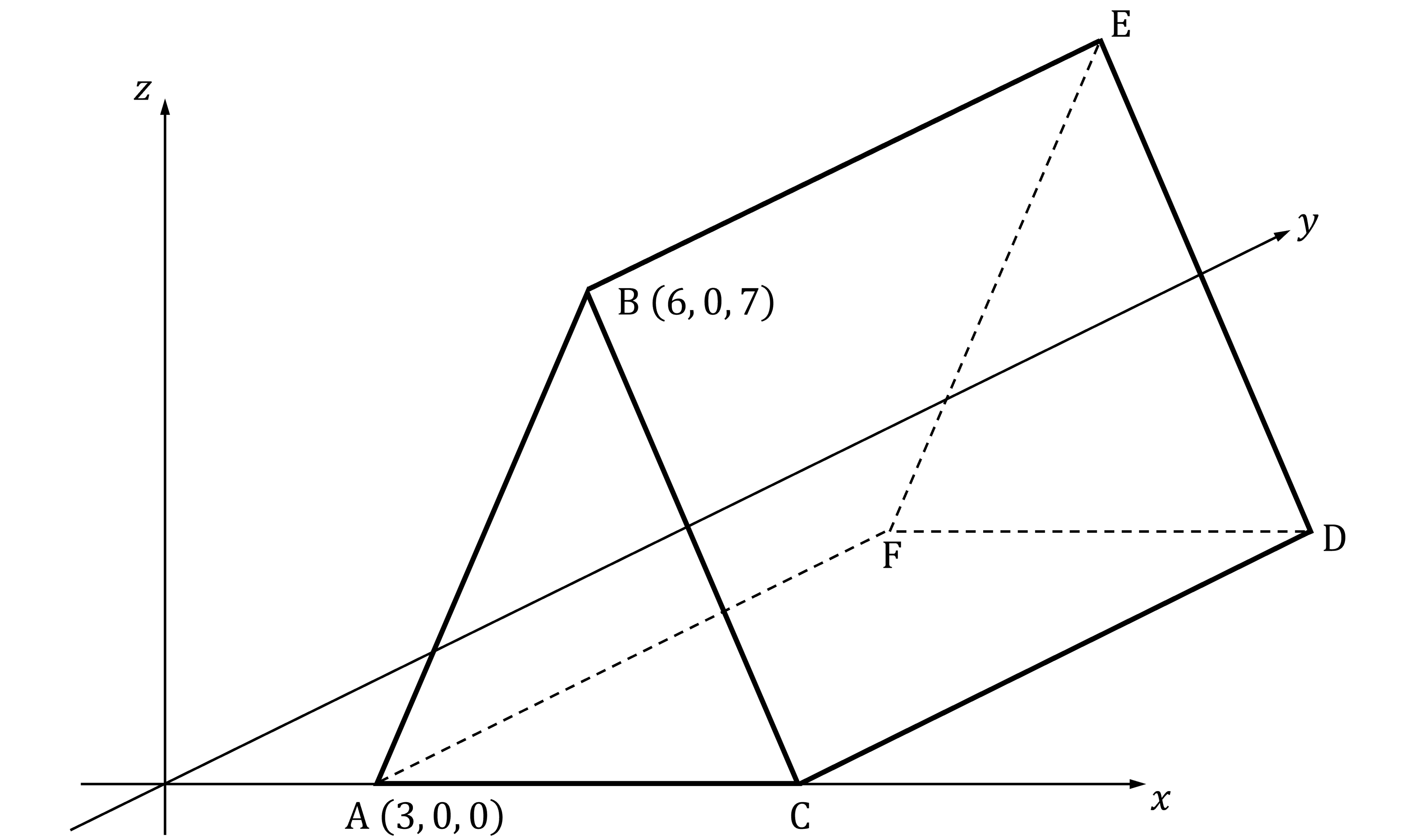
The diagram shows a triangular prism ABCDEF, relative to the coordinate axes.

3D prism ABCDEF with vertices A(3,0,0), B(6,0,7), on x, y, z axes. Includes projections and lines. Axes labelled x, y, z.

  • AB equals BC.

  • CD equals 10 space units.

  • Edges AF comma space BE and CD are parallel to the y-axis.

a) Write down the coordinates of straight E and straight D.

b) Write the vector BD with rightwards arrow on top in component form.

Answer:

Part (a)

Because ABCDEF is a triangular prism, the three edges AF comma space BE and CD all have the same length (10 units)

Because BE is parallel to the y-axis

  • straight E will have the same x and z coordinates as straight B

  • Only the space y coordinate will change (increase by 10)

straight E open parentheses 6 comma space 10 comma space 7 close parentheses

Because AB equals BC, triangle ABC is isosceles

  • This means it is symmetrical around its perpendicular height

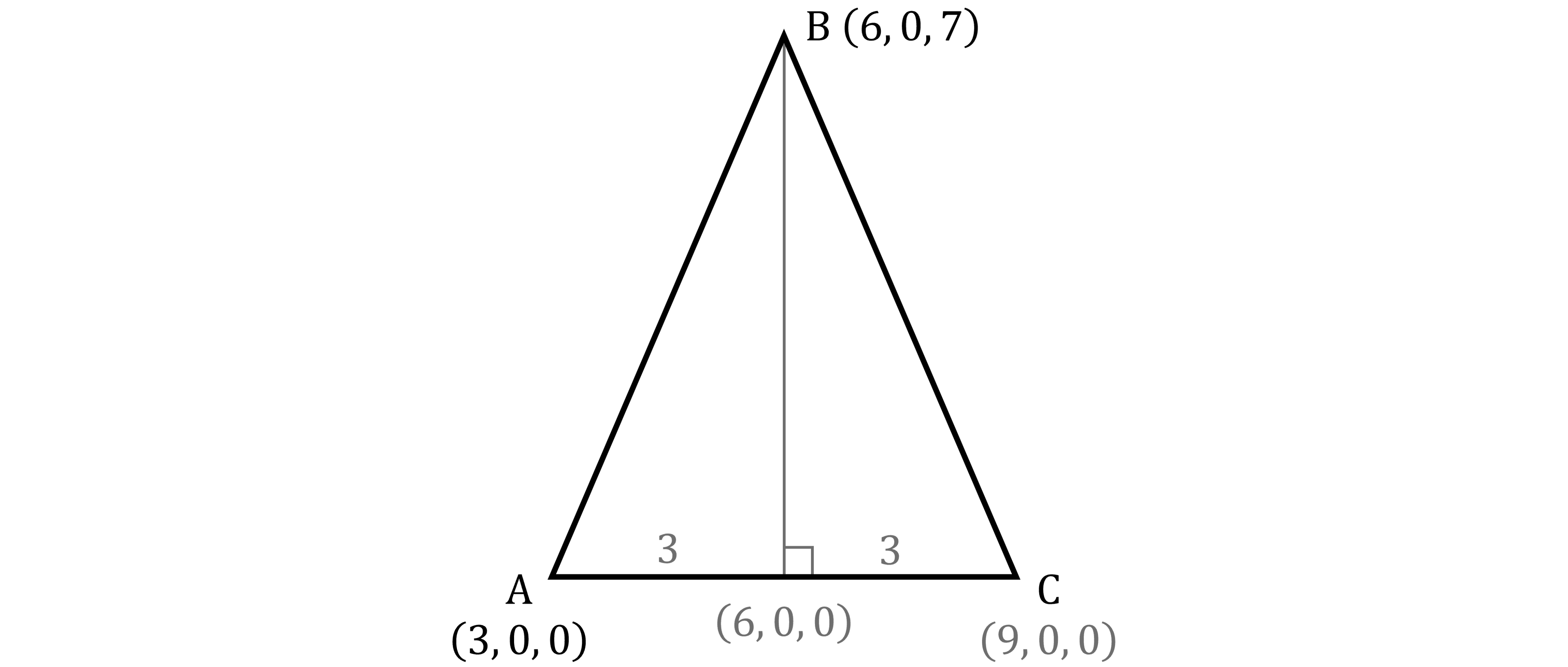
Isosceles triangle with vertices A(3,0,0), B(6,0,7), C(9,0,0). Height from B to base AC is marked with a right angle. Centre point of bass is labelled (6, 0, 0).

Then because CD is parallel to the y-axis

  • straight D will have the same x and z coordinates as straight C

  • Only the space y coordinate will change (increase by 10)

straight D open parentheses 9 comma space 10 comma space 0 close parentheses

Part (b)

To find vector BD with rightwards arrow on top in component form

  • subtract the coordinates for the first point (straight B) from the coordinates for the second point (straight D)

BD with rightwards arrow on top equals open parentheses table row cell 9 minus 6 end cell row cell 10 minus 0 end cell row cell 0 minus 7 end cell end table close parentheses

BD with rightwards arrow on top equals open parentheses table row 3 row 10 row cell negative 7 end cell end table close parentheses

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Vector PathwaysNext:Graphs of Basic Trigonometric Functions
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.