National 5MathsSQARevision NotesGeometric SkillsVolumeComposite Solids

Composite Solids (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Calculating the volume of composite solids

What are composite solids?

  • A composite solid is a 3D shape made up of more than one standard solid

    • It may be a solid made up of two or more standard solids stuck together

      • E.g. a traffic bollard in the shape of a cylinder with a hemisphere on top

    • Or it may be a standard solid from which the volume of another standard solid has been removed

      • E.g. a sculpture in the shape of a pyramid with a spherical hollow in the middle

  • Composite solid questions are often given as part of a real-life scenario

    • E.g. the volume of concrete required to make an object in the shape of a composite solid

How do I solve problems involving composite solids?

  • For these questions you will often need the volume formulae that you learned in your National 4 Maths course

    • Volume of a cube with side length l

      • V equals l cubed

    • Volume of a cuboid with length l, width w, and height h

      • V equals l cross times w cross times h

    • Volume of a cylinder with radius r and height h

      • V equals pi r squared h

    • Volume of a prism with cross-sectional area A and length l

      • V equals A cross times l

  • The object may only include part of a standard solid

    • A hemisphere is half a sphere

    • A frustum is a truncated (chopped-off) cone or pyramid

      • The volume of a frustum will be the volume of the smaller cone or pyramid subtracted from the volume of the larger cone or pyramid

  • For a composite solid

    • First find the volumes of the individual standard solids

    • Then either add them together, or subtract one from the other, depending on the question

Examiner Tips and Tricks

Read the question carefully to make sure that you are clear about

  • the precise 3D shapes involved

  • whether you should be adding or subtracting volumes

Worked Example

A concrete gatepost is made in the shape of a cuboid with a pyramid on top.

Grey cuboid with a pyramid on top, total height 2.4 metres, base width 0.44 metres, pyramid height 0.5 metres.

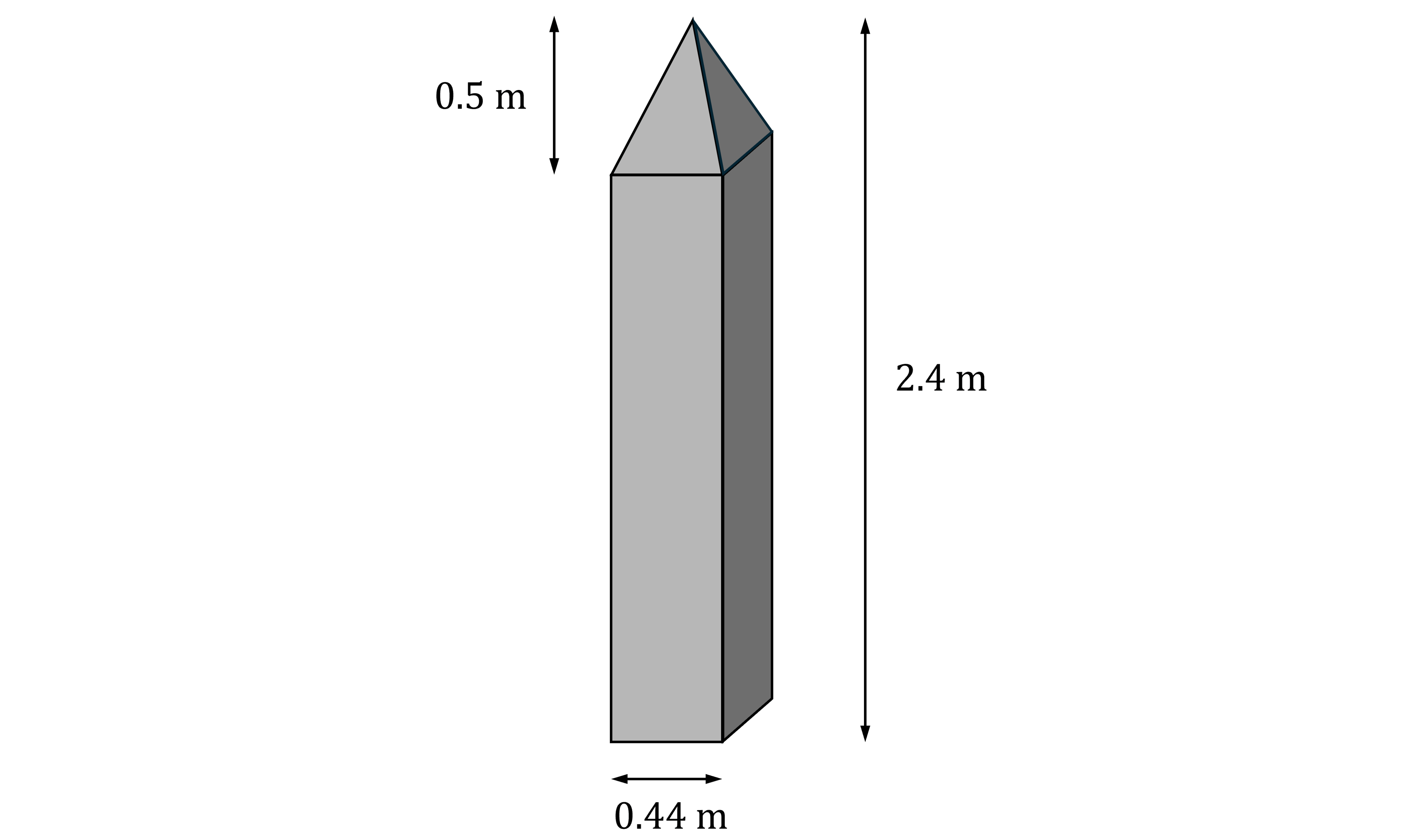
The cuboid has a square base of length 0.44 metres.

The pyramid has a height of 0.5 metres, and its base fits exactly on the top of the cuboid.

The total height of the gatepost is 2.4 metres.

Calculate the volume of concrete needed to make a gatepost.

Answer:

Start by finding the volume of the cuboid using V equals l cross times w cross times h

  • Here l equals 0.44 comma space w equals 0.44 and h equals 2.4 minus 0.5 equals 1.9

table row cell V subscript C end cell equals cell 0.44 cross times 0.44 cross times 1.9 end cell row blank equals cell 0.36784 end cell end table

Next find the volume of the pyramid using V equals 1 third A h

  • Here h equals 0.5

  • And the base is an square with area A equals 0.44 cross times 0.44

table row cell V subscript P end cell equals cell 1 third cross times 0.44 cross times 0.44 cross times 0.5 end cell row blank equals cell 0.032266... end cell end table

Find the sum

table row cell V subscript C plus V subscript P end cell equals cell 0.36784 plus 0.032266... end cell row blank equals cell 0.400106... end cell end table

Round to a sensible degree of accuracy

  • If a question doesn't specify, 3 significant figures is usually a good choice

Don't forget to include units in your final answer

0.400 m3 (3 s.f.)

Worked Example

A wooden block is in the shape of a large cone with a small cone removed.

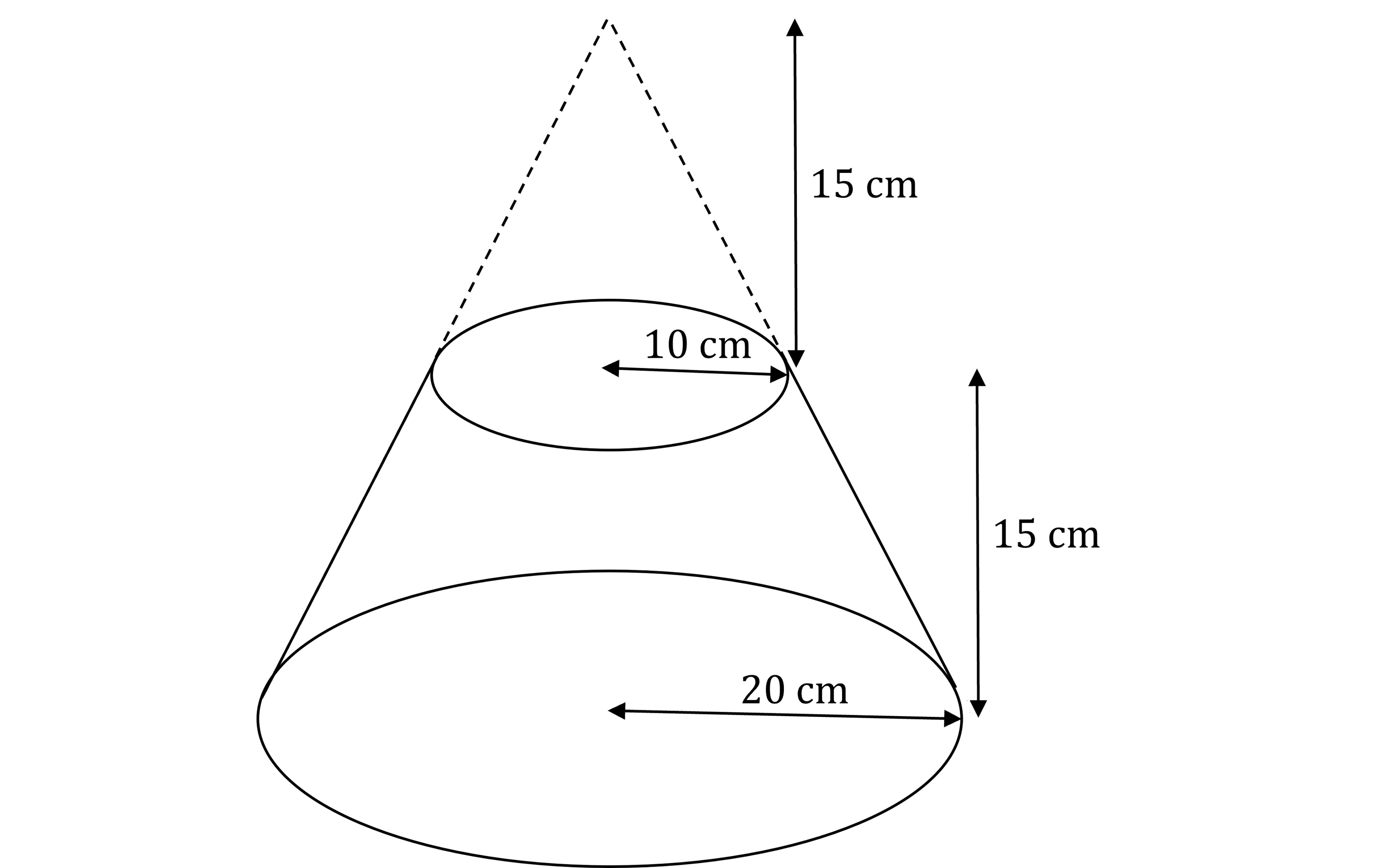
Diagram of a frustum of a cone, with top radius 10 cm, bottom radius 20 cm, and height 15 cm. The height of the 'missing' upper cone is 15 cm.

The large cone has a base radius of 20 centimetres.

The small cone has a base radius of 10 centimetres and a height of 15 centimetres.

The block has a height of 15 centimetres.

Calculate the volume of the block, and round the final answer to 3 significant figures.

Answer:

Start by finding the volume of the two cones using V equals 1 third pi r squared h

For the small cone, r equals 10 and h equals 15

table row cell V subscript S end cell equals cell 1 third pi cross times 10 squared cross times 15 end cell row blank equals cell 500 pi end cell end table

It's best to keep that exact value for now, and only round when giving the final answer

For the large cone, r equals 20 and h equals 15 plus 15 equals 30

table row cell V subscript L end cell equals cell 1 third pi cross times 20 squared cross times 30 end cell row blank equals cell 4000 pi end cell end table

Find the difference

table row cell V subscript L minus V subscript S end cell equals cell 4000 pi minus 500 pi end cell row blank equals cell 3500 pi end cell row blank equals cell 10 995.5742... end cell end table

Round to 3 significant figures, as required, and don't forget to include units

11 000 cm3 (3 s.f.)

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Sphere, Cone & PyramidNext:Converse of Pythagoras' Theorem
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.