National 5MathsSQARevision NotesGeometric SkillsVolumeSphere, Cone & Pyramid

Sphere, Cone & Pyramid (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Calculating the volume of standard solids

What is volume?

  • The volume of a 3D shape is a measure of how much space it takes up

  • You need to be able to calculate the volumes of a number of standard solids:

    • Spheres

    • Cones

    • Pyramids

Examiner Tips and Tricks

From your National 4 Maths course, you should also be familiar with calculating the volumes of cubes, cuboids, prisms and cylinders.

How do I find the volume of a sphere?

  • To calculate the volume, V, of a sphere with radius r, use the formula

    • V equals 4 over 3 pi r cubed

    • This formula is given to you in your exam

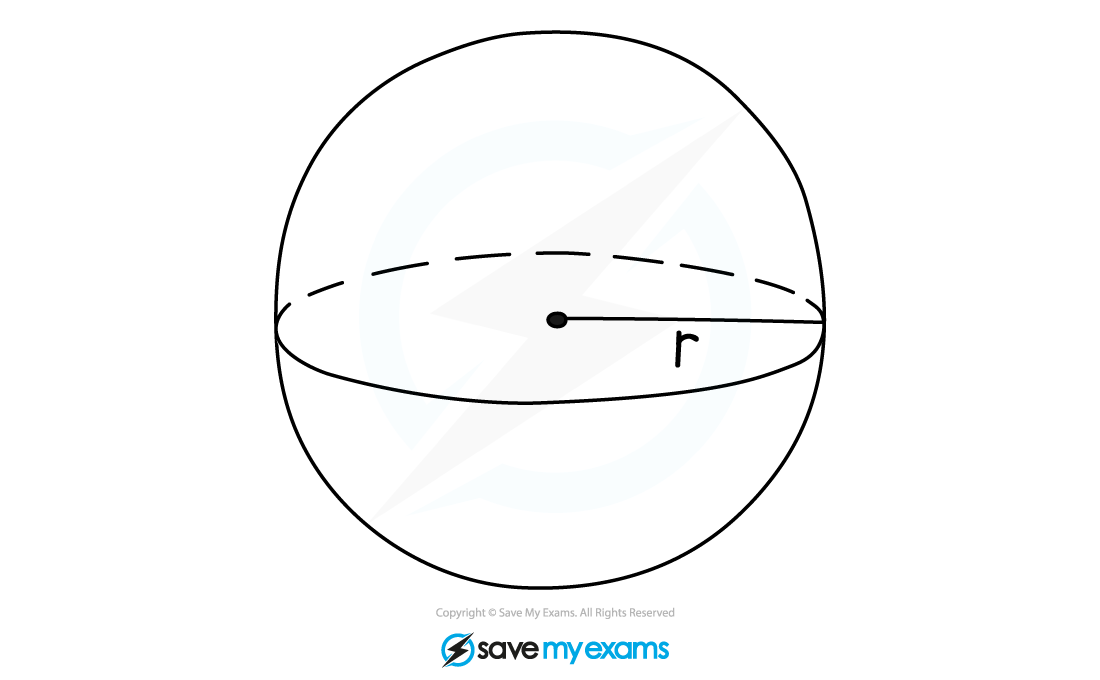
Sphere Radius r, IGCSE & GCSE Maths revision notes

  • A hemisphere is half of a sphere

    • If you need to find the volume of a hemisphere

      • Find the volume of a sphere with the same radius

      • and divide it by 2 (or multiply it by 1 half)

How do I find the volume of a cone?

  • To calculate the volume, V, of a cone with base radius r, and perpendicular height h, use the formula

    • V equals 1 third pi r squared h

    • This formula is given to you in your exam

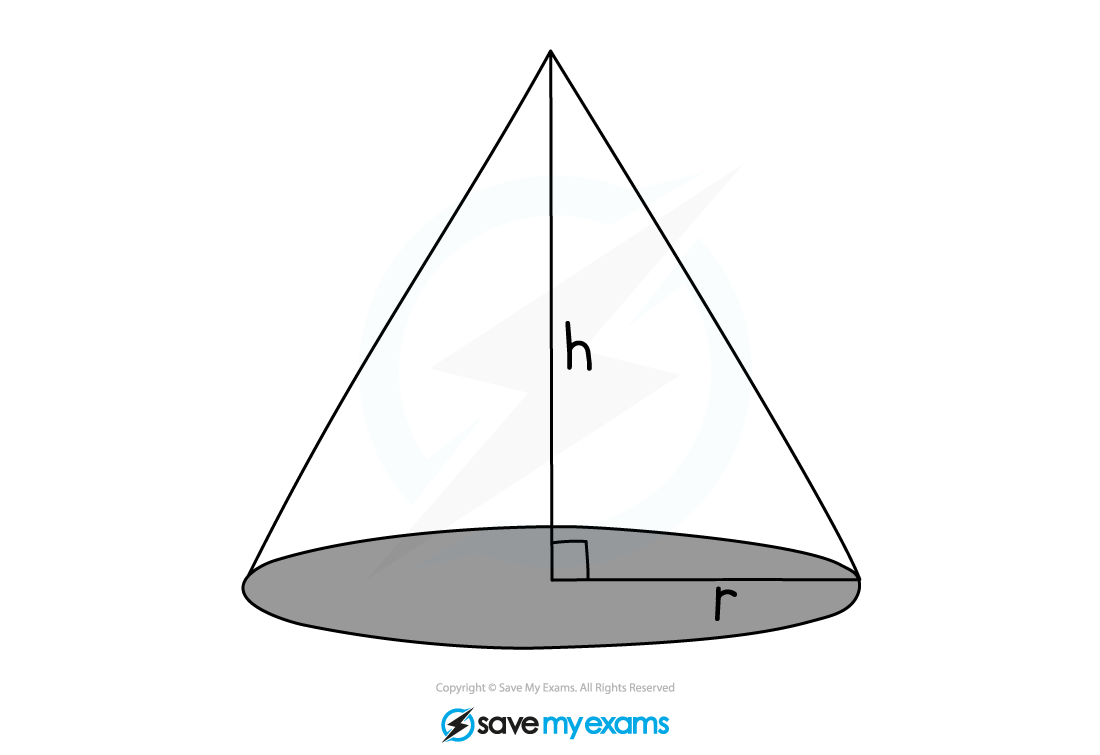
Cone volume, IGCSE & GCSE Maths revision notes

  • The height must be a line from the top of the cone that is perpendicular to the base

How do I find the volume of a pyramid?

  • To calculate the volume, V, of a pyramid with base area A, and perpendicular height h, use the formula

    • V equals 1 third A h

    • This formula is given to you in your exam

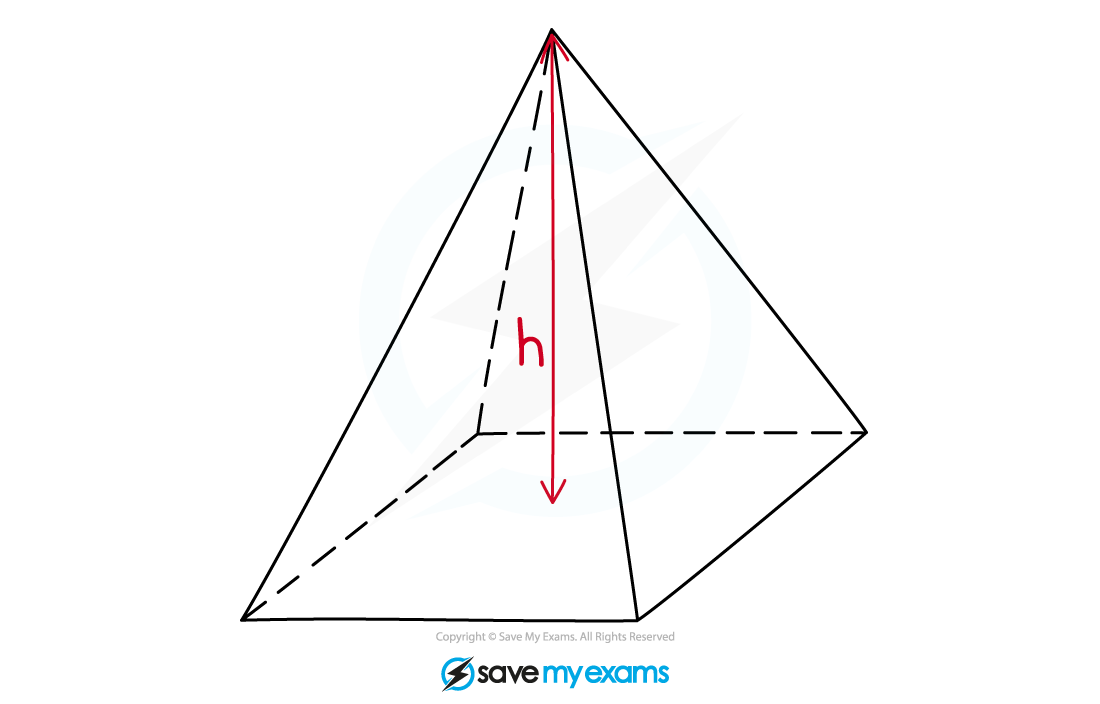
Volume of a pyramid

  • Note that volume formula for a pyramid is similar to the volume formula for a cone

  • The height must be a line from the top of the pyramid that is perpendicular to the base

  • The base of a pyramid could be a square, a rectangle or a triangle

Examiner Tips and Tricks

The volume formulae for spheres, cones and pyramids are all included on the Formulae List in the exam paper.

Examiner Tips and Tricks

Be careful with sphere and cone questions.

  • The question may give you the diameter instead of the radius

  • Remember to halve the diameter to find the radius before substituting into the formula

Worked Example

A sphere has a diameter of 9 centimetres.

Calculate the volume of the sphere, and round the final answer to 3 significant figures.

Answer:

The sphere's diameter is 9 cm

  • This means the radius, r, is 9 over 2 equals4.5 cm

Use the formula for volume of a sphere, V equals 4 over 3 pi r cubed

V equals 4 over 3 cross times pi cross times 4.5 cubed

Use your calculator to evaluate that

equals 381.703507...

Round to 3 significant figures, as required, and don't forget to include units

382 cm3 (3 s.f.)

Worked Example

The diagram below shows a cone with diameter 20 centimetres and height 90 centimetres.

Diagram of a cone with a height of 90 cm and a base diameter of 20 cm, featuring labelled dimensions and a central dot on the base.

Without using a calculator, calculate the volume of the cone.

Take bold italic pi bold equals bold 3 bold. bold 14.
 

Answer:

The cone's base diameter is 20 cm

  • This means the radius, r, is 20 over 2 equals10 cm

Use the formula for volume of a cone, V equals 1 third pi r squared h

  • Use pi equals 3.14, as the question says

table row V equals cell 1 third cross times 3.14 cross times 10 squared cross times 90 end cell row blank equals cell 1 third cross times 90 cross times 10 squared cross times 3.14 end cell end table

1 third cross times 90 equals 30 and 10 squared equals 100

table row blank equals cell 30 cross times 100 cross times 3.14 end cell row blank equals cell 3000 cross times 3.14 end cell row blank equals cell 3 cross times 3.14 cross times 1000 end cell row blank equals cell 9.42 cross times 1000 end cell row blank equals 9420 end table

Don't forget to include units in your final answer

9420 cm3

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Problem Solving with Arcs & SectorsNext:Composite Solids
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.