National 5MathsSQARevision NotesTrigonometric SkillsGraphs of Trigonometric FunctionsCombinations of Transformations

Combinations of Transformations (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Combinations of transformations

  • Exam questions will usually include multiple transformations of a trigonometric graph

Examiner Tips and Tricks

When combining transformations, vertical transformations (change of amplitude, vertical translation) and horizontal transformations (multiple angle, phase angle) are independent of each other

  • If you combine a vertical transformation with a horizontal transformation, it doesn't matter what order you make the changes to the graph

However transformations of the same sort (vertical or horizontal) do affect each other

  • So if you combine two vertical transformations, for example, you have to make the changes to the graph in the correct order to get the correct result

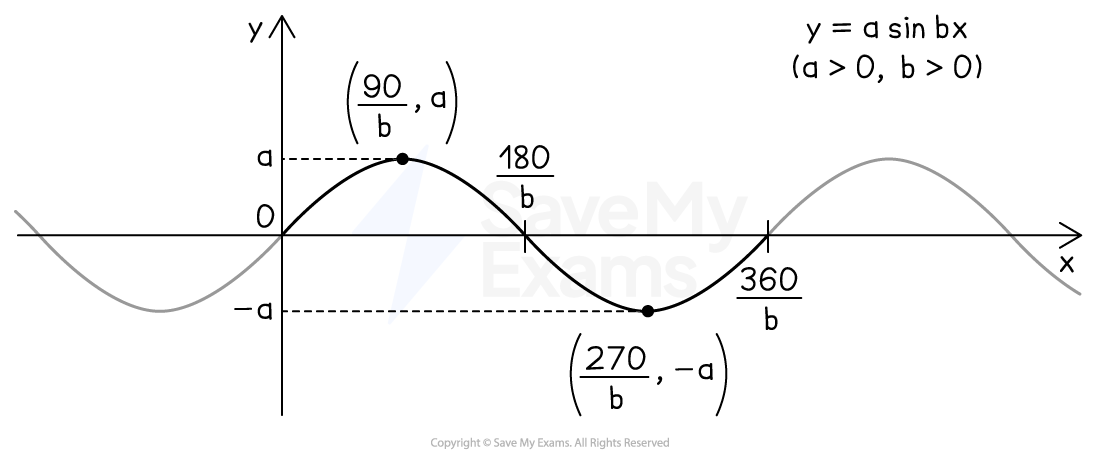
asinbx and acosbx

  • Transformations of this form combine a change of amplitude (vertical stretch) and a multiple angle (horizontal stretch)

    • The amplitude and the y-coordinates of minimum and maximum turning points are the same as for space a sin x and space a cos x

    • The period and the x-coordinates of roots and minimum and maximum turning points are the same as for sin b x and cos b x

  • For example, the graph of space a sin b x looks like this:

Graph of y = a sin bx, showing curve peak at (90/b, a) and trough at (270/b, -a) with axes marked x and y. The x-axis crossings are marked at x=180/b and x=360/b. Constants a, b > 0.

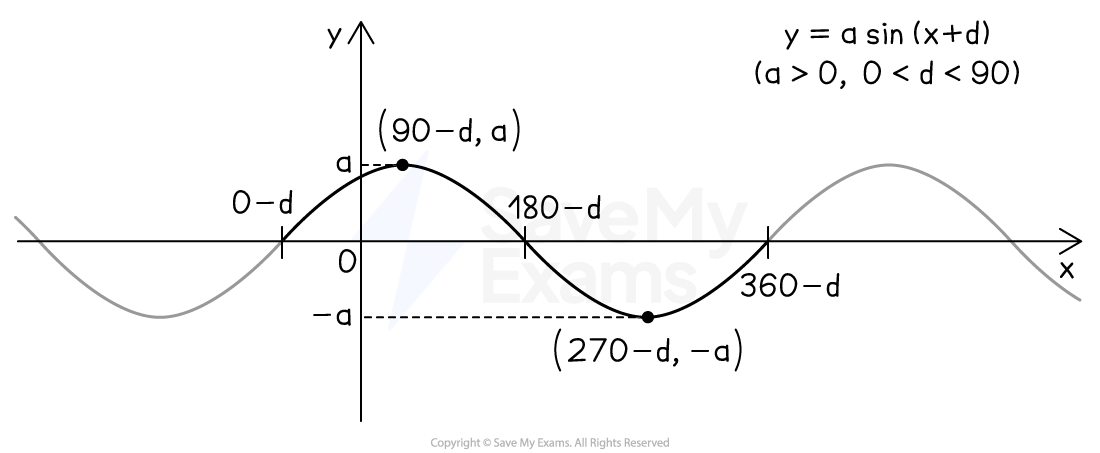
asin(x+d) and acos(x+d)

  • Transformations of this form combine a change of amplitude (vertical stretch) and a phase angle (horizontal translation)

    • The period is 360°

    • The amplitude and the y-coordinates of minimum and maximum turning points are the same as for space a sin x and space a cos x

    • The x-coordinates of roots and minimum and maximum turning points are the same as for sin open parentheses x plus d close parentheses and cos open parentheses x plus d close parentheses

  • For example, when bold italic d is negative the graph of space a sin open parentheses x plus d close parentheses looks like this

    • Remember, if d is negative, this means a shift to the right

      • E.g. if the graph is of space 2 sin open parentheses x minus 30 close parentheses

        • The graph will 'start' at x equals 0 minus open parentheses negative 30 close parentheses equals 30 degree

        • The first maximum turning point will be at x equals 90 minus open parentheses negative 30 close parentheses equals 120 degree

Graph of the function y = a sin(x + d) for a > 0 and d < 0. Maximum turning point labelled at (90-d, a) and minimum turning point labelled at (270-d, a). The x-axis crossing points are labelled 0-d, 180-d and 360-d.

sin(x+d)+c and sin(x+d)+c

  • Transformations of this form combine a vertical translation and a phase angle (horizontal translation)

    • The period is 360°

    • The amplitude is 1

    • The y-coordinates of minimum and maximum turning points and of the 'middle line' are the same as for space sin x plus c and space cos x plus c

    • The x-coordinates of roots and minimum and maximum turning points are the same as for sin open parentheses x plus d close parentheses and cos open parentheses x plus d close parentheses

sin(bx)+c and cos(bx)+c

  • Transformations of this form combine a vertical translation and a multiple angle (horizontal stretch)

    • The amplitude is 1

    • The y-coordinates of minimum and maximum turning points and of the 'middle line' are the same as for space sin x plus c and cos x plus c

    • The period and the x-coordinates of roots and minimum and maximum turning points are the same as for sin b x and cos b x

asinx+c and acosx+c

  • Transformations of this form combine a change of amplitude (vertical stretch) and a vertical translation

    • Both transformations are vertical

    • The change of amplitude happens before the vertical translation

  • For example, for 2 sin x minus 4

    • There is a stretch by a factor of 2, then a translation 4 units down

      • The amplitude is 2 (vertical translation doesn't affect amplitude)

      • The period is 360° (vertical changes don't affect the period)

    • To find coordinates of important points, multiply the y-coordinate by 2, then add 4 (the x-coordinates don't change)

      • The graph 'starts' at open parentheses 0 comma space 2 cross times 0 minus 4 close parentheses equals open parentheses 0 comma space minus 4 close parentheses

      • The first maximum turning point occurs at open parentheses 90 comma space 2 cross times 1 minus 4 close parentheses equals open parentheses 90 comma space minus 2 close parentheses

sin(bx+d) and cos(bx+d)

  • Transformations of this form combine a multiple angle (horizontal stretch) and a phase angle (horizontal translation)

    • Both transformations are horizontal

    • The horizontal translation (phase angle) happens before the horizontal stretch (multiple angle)

  • For example, for cos open parentheses 2 x plus 30 close parentheses

    • There is a translation 30° left, then a stretch by a factor of 1 half

      • The amplitude is 1 (horizontal changes don't affect amplitude)

      • The period is 360 over 2=180° (horizontal translation doesn't affect period)

    • To find coordinates of important points, subtract 30 from the x-coordinate by 2, then divide by 2 (the y-coordinates don't change)

      • The graph 'starts' at open parentheses fraction numerator 0 minus 30 over denominator 2 end fraction comma space 1 close parentheses equals open parentheses negative 15 comma space 1 close parentheses

      • The first minimum turning point occurs at open parentheses fraction numerator 180 minus 30 over denominator 2 end fraction comma space minus 1 close parentheses equals open parentheses 75 comma space minus 1 close parentheses

Examiner Tips and Tricks

It is possible to combine more than two transformations, although as of 2025 there are no examples of this occurring on an exam.

If you need to combine more than two transformations, follow the procedures above remembering that

  • for two vertical transformations, change of amplitude happens before vertical translation

  • for two horizontal transformations, horizontal translation (phase angle) happens before horizontal stretch (multiple angle)

Finding equations or coordinates of transformed graphs

How do I find equations or coordinates of points from transformed trigonometric graphs?

  • On the exam, questions on this topic are usually of one of two forms

    • You are given a graph with definite coordinates, and asked to find the corresponding equation in a certain form

    • You are given the trigonometric equation and asked to find the coordinates for a particular point on the corresponding graph

Finding equations

  • To find an equation, the key is to

    • compare features of the graph (for example the period, the amplitude, or the coordinates of a turning point)

    • with what those features should be in terms of the variables in the equation

  • For example, if you know the equation is in the form space y equals a cos b x, and you can see that the graph has a maximum turning point at (0, 7) and completes two cycles between 0 and 360°

    • The graph of cos x has been vertically stretched by a factor of a and horizontally stretched by a factor of 1 over b to get the graph of space a cos b x

    • The amplitude of space a cos b x is a, and it should therefore have a maximum point at open parentheses 0 comma space a close parentheses

      • So a equals 7

    • The period of space a cos b x is open parentheses 360 over b close parentheses to the power of degree and the period of the graph is 180° (2 cycles in 360°)

      • So 180 equals 360 over b space space rightwards double arrow space space b equals 360 over 180 equals 2

    • The equation is space y equals 7 cos 2 x

Finding coordinates

  • To find coordinates

    • determine what the coordinates of the point on the graph should be

    • based on the numbers used in the equation

  • For example, if you know that the equation is y equals 3 sin open parentheses x minus 60 close parentheses, and you are asked to find the coordinates of the first maximum point

    • The graph of sin x has been vertically stretched by a factor of 3 and horizontally translated 60° to the right to get the graph of 3 sin open parentheses x minus 60 close parentheses

    • So instead of being at (90°, 1), the first maximum point should be at

      • open parentheses 90 minus open parentheses negative 60 close parentheses comma space 1 cross times 3 close parentheses equals open parentheses 150 degree comma space 3 close parentheses

Worked Example

Part of the graph of space y equals sin open parentheses x plus a close parentheses degree plus b is shown.

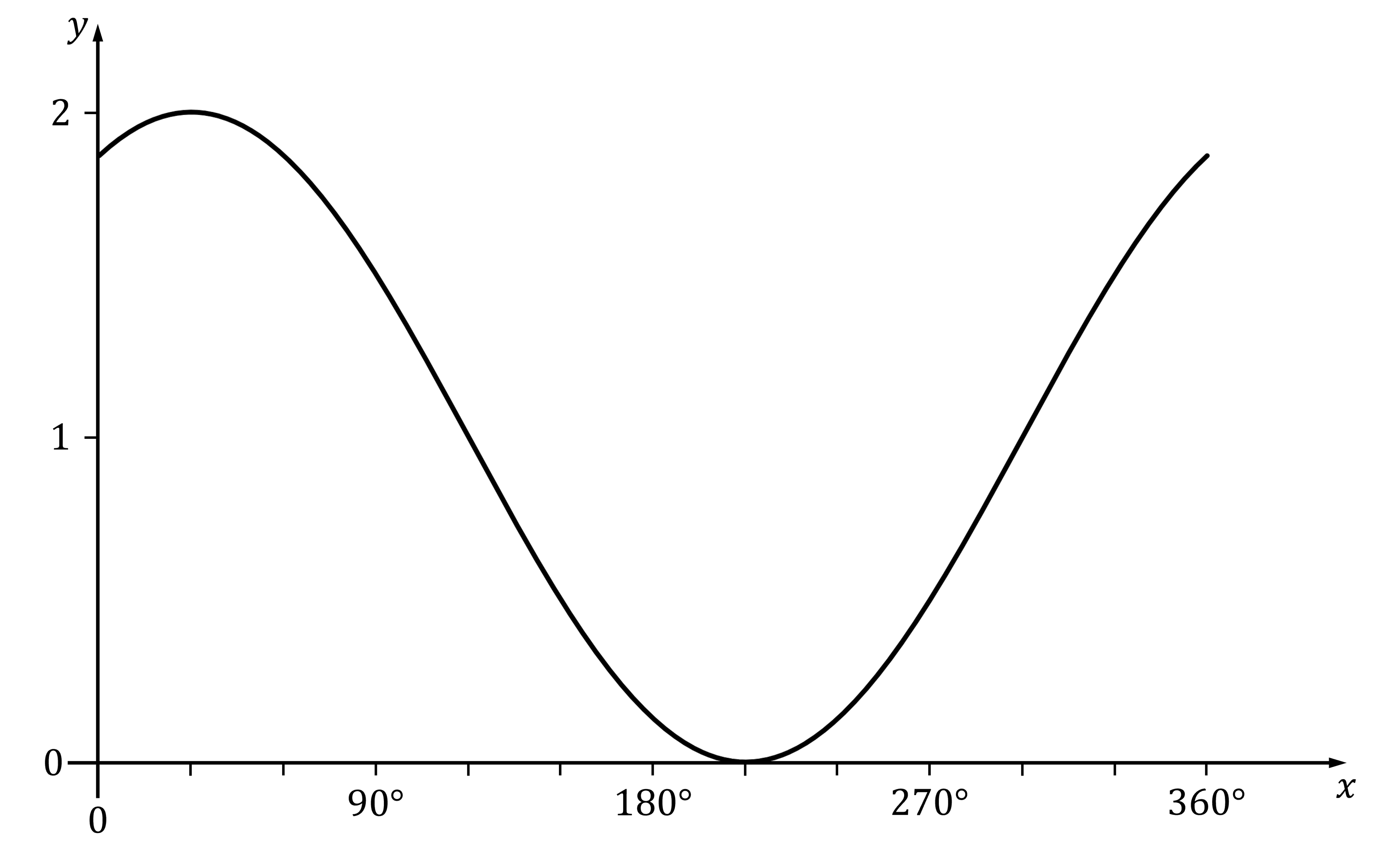
Graph showing a sinusoidal wave, starting a bit below y=2 at x=0, increasing to a maximum, then decreasing to a minimum of y=0 at 210° before rising again. The x-axis is labelled in degrees between 0° and 360°, and the y-axis is labelled at 1 and 2.

(a) State the value of a.

(b) State the value of b.

Answer:

The key here is to note the coordinates of the minimum turning point at open parentheses 210 degree comma space 0 close parentheses

Compared to y equals sin x, the graph of space y equals sin open parentheses x plus a close parentheses plus b involves

  • a horizontal translation by |a|° (to the left if a is positive, and to the right if a is negative)

  • a vertical translation by |b| units (up if b is positive, and down if b is negative)

The graph of y equals sin x has its first minimum point at open parentheses 270 degree comma space minus 1 close parentheses; compared to that the minimum point on space y equals sin open parentheses x plus a close parentheses plus b has

  • moved 60° to the left (so a is positive)

  • moved 1 unit up (so b is also positive)

Part (a)

a = 60

Part (b)

b = 1

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Transformations of Trigonometric GraphsNext:Mean & Standard Deviation
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.