National 5MathsSQARevision NotesTrigonometric SkillsTrigonometric Equations & IdentitiesPeriod & Related Angles

Period & Related Angles (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

What are the periods of the trigonometric functions?

  • The periods of the basic trigonometric functions are discussed at Graphs of Basic Trigonometric Functions

  • bold italic y bold equals bold sin bold italic x has a period of 360° (it repeats every 360°)

    • If sin x has some value for x equals a

      • then it has that same value for x equals a plus 360 degree comma space a plus 720 degree comma etc.

      • and also for x equals a minus 360 degree comma space a minus 720 degree comma etc.

    • E.g. sin open parentheses 30 close parentheses equals 0.5

      • so sin open parentheses 390 close parentheses is also equal to 0.5

  • bold italic y bold equals bold cos bold italic x also has a period of 360° (it repeats every 360°)

    • If cos x has some value for x equals a

      • then it has that same value for x equals a plus 360 degree comma space a plus 720 degree comma etc.

      • and also for x equals a minus 360 degree comma space a minus 720 degree comma etc.

    • E.g. cos open parentheses 60 close parentheses equals 0.5

      • so cos open parentheses 420 close parentheses is also equal to 0.5

  • bold italic y bold equals bold tan bold italic x has a period of 180° (it repeats every 180°)

    • If tan x has some value for x equals a

      • then it has that same value for x equals a plus 180 degree comma space a plus 360 degree comma etc.

      • and also for x equals a minus 180 degree comma space a minus 360 degree comma etc.

    • E.g. tan open parentheses 45 close parentheses equals 1

      • so tan open parentheses 225 close parentheses is also equal to 1

  • The sin and cos functions are both symmetric

    • This symmetry allows you to find other values for x that give the same values of sin or cos

  • These 'other values of x' are known as related angles

  • Sketch the sine graph for the given interval

    • Identify the first value on the graph

      • then use the symmetry of the graph to find additional values

    • E.g. if you know sin open parentheses 30 close parentheses equals 0.5 and want to find other values of xfor which sin x equals 0.5, where 0 degree less or equal than x less or equal than 360 degree

      • Sketch the graph y equals sin space x for 0 degree less or equal than x less or equal than 360 degree

      • Draw on sin open parentheses 30 close parentheses equals 0.5

      • By symmetry, another value of x is 180 degree minus 30 degree equals 150 degree

      • sin open parentheses 150 close parentheses is also equal to 0.5

Graph of y=sin(x) from x=0º to x=360º. The graph shows vertical lines at 30º and 150º that meet the curve at y=0.5.

  • Sketch the cosine graph for the given interval

    • Identify the first value on the graph

      • then use the symmetry of the graph to find additional values

    • E.g. if you know cos open parentheses 60 close parentheses equals 0.5 and want to find other values of xfor which cos x equals 0.5, where 0 degree less or equal than x less or equal than 360 degree

      • Sketch the graph y equals cos space x for 0 degree less or equal than x less or equal than 360 degree

      • Draw on cos open parentheses 60 close parentheses equals 0.5

      • By symmetry, another value of x is 360 degree minus 60 degree equals 300 degree

      • cos open parentheses 300 close parentheses is also equal to 0.5

Graph of y=cos(x) from x=0º to x=360º. The graph shows vertical lines at 60º and 300º that meet the curve at y=0.5.

Worked Example

Given that cos 60 degree equals 0.5, state the value of cos 240 degree.

Answer:

Sketch space y equals cos x and use symmetry to work out the value of cos 240 degree

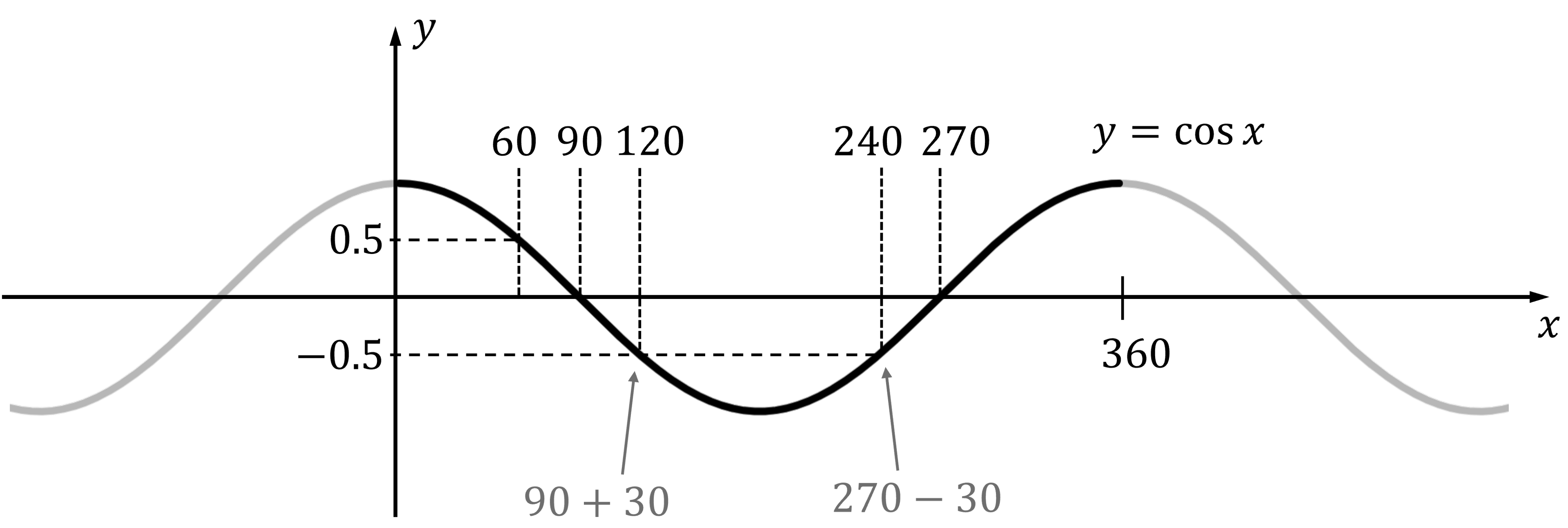
Graph of the cosine function, y = cos(x), showing a wave from 0 to 360 degrees with key points at 60, 90, 120, 240, and 270 degrees. Horizontal lines at y=0.5 and y=-0.5 are also drawn.

  • cos 60 degree equals 0.5, and 60° is 30° to the left of x equals90°

    • so 30° to the right of 90°, cos x is equal to negative 0.5

    • i.e. cos 120 degree equals negative 0.5

  • 120° is 30° to the right of x equals90°

    • so 30° to the left of 270°, cos x is also equal to negative 0.5

    • i.e. cos 240 degree equals negative 0.5

cos 240 degree equals negative 0.5

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Combinations of TransformationsNext:Trigonometric Equations
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.