National 5MathsSQARevision NotesTrigonometric SkillsTrigonometric Equations & IdentitiesTrigonometric Equations

Trigonometric Equations (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Solving trigonometric equations

What are trigonometric equations?

  • Trigonometric equations are equations involving sin space x, cos space x and tan space x

  • They often have multiple solutions

    • A calculator gives the first solution

    • You need to use periods and related angles to find the others

    • The solutions you find must lie in the interval (range) of x given in the question, e.g. 0 degree less or equal than x less or equal than 360 degree

How do I solve sin x = ...?

  • Find the first solution of the equation by taking the inverse sin function on your calculator (or using an exact trig value if you know them)

    • E.g. For the first solution of the equation sin space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • This gives x equals sin to the power of negative 1 end exponent open parentheses 0.5 close parentheses equals 30 degree

  • Use the symmetry of the sine function and related angles to find other solutions

    • If x equals 30 degree is a solution, then by symmetry x equals 180 minus 30 equals 150 degree is another solution

    • If necessary you can also use the period of sin x to find additional solutions

      • Adding or subtracting 360° to a solution gives another solution

  • You can use a calculator to check the solutions

    • E.g. For the equation sin space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • Substitute x equals 30 degree and x equals 150 degree in to the calculator

      • sin open parentheses 30 close parentheses and sin open parentheses 150 close parentheses both give a value of 0.5, so are correct

Examiner Tips and Tricks

In general, if x is an acute solution to sin space x equals... (i.e. if 0 degree less than x less than 90 degree)

  • then 180 minus x is an obtuse solution to the same equation.

How do I solve cos x = ...?

  • Find the first solution of the equation by taking the inverse cos function (or using an exact trig value if you know them)

    • E.g. For the first solution of the equation cos space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • This gives x equals cos to the power of negative 1 end exponent open parentheses 0.5 close parentheses equals 60 degree

  • Use the symmetry of the cosine function and related angles to find other solutions

    • If x equals 60 degree is a solution, then by symmetry x equals 360 minus 60 equals 300 degree is another solution

    • If necessary you can also use the period of cos x to find additional solutions

      • Adding or subtracting 360° to a solution gives another solution

  • You can use a calculator to check the solutions

    • E.g. For the equation cos space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • Substitute x equals 60 degree and x equals 300 degree in to the calculator

      • cos open parentheses 60 close parentheses and cos open parentheses 300 close parentheses both give a value of 0.5 so are correct

Examiner Tips and Tricks

In general, if x is a solution to cos space x equals...

  • then 360 minus x is another solution to the same equation

How do I solve tan x = ...?

  • Find the first solution of the equation by taking the inverse tan function (or using an exact trig value if you know them)

    • E.g. For the first solution of the equation tan space x equals 1 for 0 degree less or equal than x less or equal than 360 degree

      • This gives x equals tan to the power of negative 1 end exponent open parentheses 1 close parentheses equals 45 degree

  • Use the period of the tan function to find other solutions

    • Adding or subtracting 180° to a solution gives another solution

    • If x equals 45 degree is a solution, then by symmetry x equals 45 plus 180 equals 225 degree is another solution

  • You can use a calculator to check the solutions

    • E.g. For the equation tan space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • Substitute x equals 45 degree and x equals 225 degree in to the calculator

      • tan open parentheses 45 close parentheses and tan open parentheses 225 close parentheses both give a value of 1 so are correct

Examiner Tips and Tricks

In general, if x is a solution to tan space x equals...

  • Then x plus 180 is another solution to the same equation

How do I rearrange trig equations?

  • Trig equations may be given in a different form

    • Equations may require rearranging first

      • E.g. 2 space sin space x minus 1 equals 0 can be rearranged to sin x equals 0.5

    • They can then be solved as usual

What do I do if the first solution from my calculator is negative?

  • Sometimes the first solution given by the calculator for xwill be negative

    • E.g space x equals sin to the power of negative 1 end exponent open parentheses negative 0.5 close parentheses equals negative 30 degree

  • In that case, use the period to find a positive solution

    • The period of sin x is 360°

    • So negative 30 plus 360 equals 330 degree is another solution

  • Once you have a positive solution, you can use related angles to find any other positive solutions in the interval

Examiner Tips and Tricks

Know how to use the inverse functions on your calculator (sin-1, cos-1 and tan-1).

Remember you can check your solutions by substituting them back into the original equation.

Worked Example

Solve the equation space 16 sin x degree plus 7 equals 11 space, for 0 less or equal than x less than 360.

Answer:

Start by rearranging the equation into sin x equals... form

table row cell 16 sin x plus 7 end cell equals 11 row cell 16 sin x end cell equals cell 11 minus 7 end cell row cell 16 sin x end cell equals 4 row cell sin x end cell equals cell 4 over 16 end cell row cell sin x end cell equals cell 0.25 end cell end table

Use sin-1 in your calculator to find the first solution

x equals sin to the power of negative 1 end exponent open parentheses 0.25 close parentheses equals 14.477512...

Use the symmetry of the sine curve and related angles to find any other solutions

  • Sketch the graph of y equals sin space x

  • Mark on (roughly) where x equals 14.48 and y equals 0.25 would be

  • Draw a vertical line up to the curve

  • Draw another line horizontally across to the next point on the curve

  • Bring a line vertically back down to the x-axis

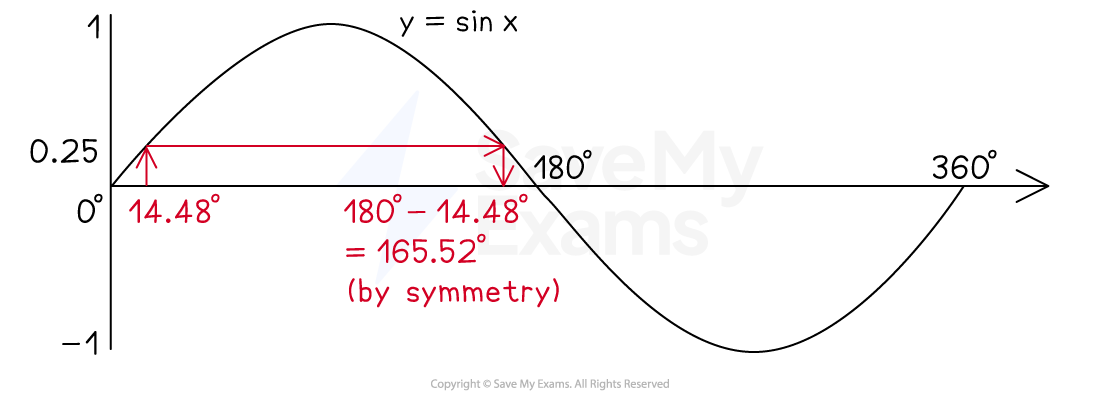
Graph of y = sin(x) from x=0º to x=360º.

Find this value using by subtracting your first solution 180

180 minus 14.477512... equals 165.522487...

Round to a sensible degree of accuracy

  • Unless a question tells you otherwise, 1 decimal place is usually a good choice for angles

x equals 14.5 degree space space or space space x equals 165.5 degree space space open parentheses 1 space straight d. straight p. close parentheses

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Period & Related AnglesNext:Trigonometric Identities
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.