National 5MathsSQARevision NotesTrigonometric SkillsTrigonometry with TrianglesArea of a Triangle

Area of a Triangle (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Calculating the area of a triangle

How do I find the area of a non-right-angled triangle?

  • The area of any triangle can be found using the formula

Area equals 1 half a b sin C space

  • C is the angle between sides a and b

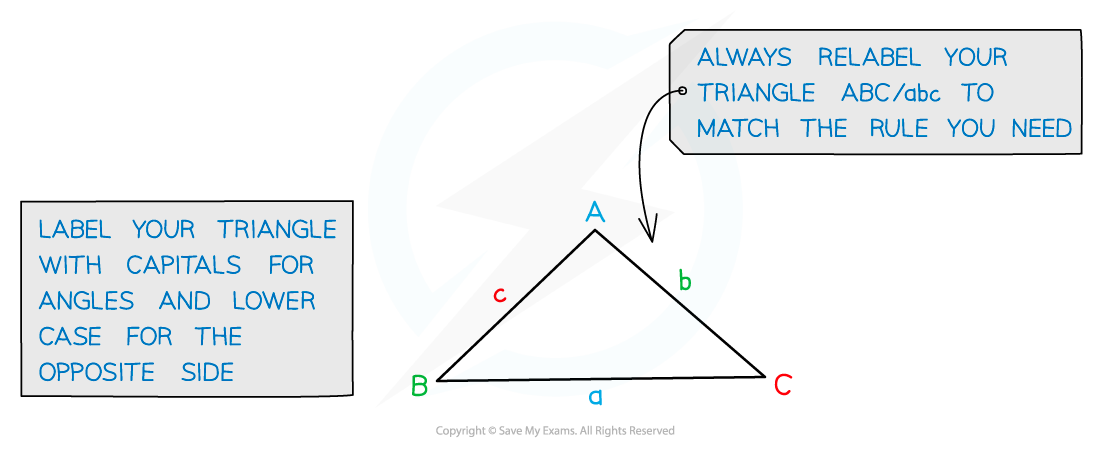
Non Right-Angled Triangle labelled with angles A, B and C and opposite corresponding sides a, b and c.

  • If angle C is 90°, you get a right-angled triangle

    • sin 90° = 1 so the formula becomes the familiar "Area = ½ × base × height"!

Examiner Tips and Tricks

Swapping the letters around allows the triangle area formula to be written in these forms as well:

Area equals 1 half a c sin B space

Area equals 1 half b c sin A space

Just make sure the angle used in the formula is in between the two sides used.

Examiner Tips and Tricks

The area of a triangle formula appears on the Formulae List in the exam paper in the form

A equals 1 half a b sin C space

Remember that the A there is for 'Area'. It is not referring to an angle labelled A!

Worked Example

Triangle ABC is shown in the diagram.

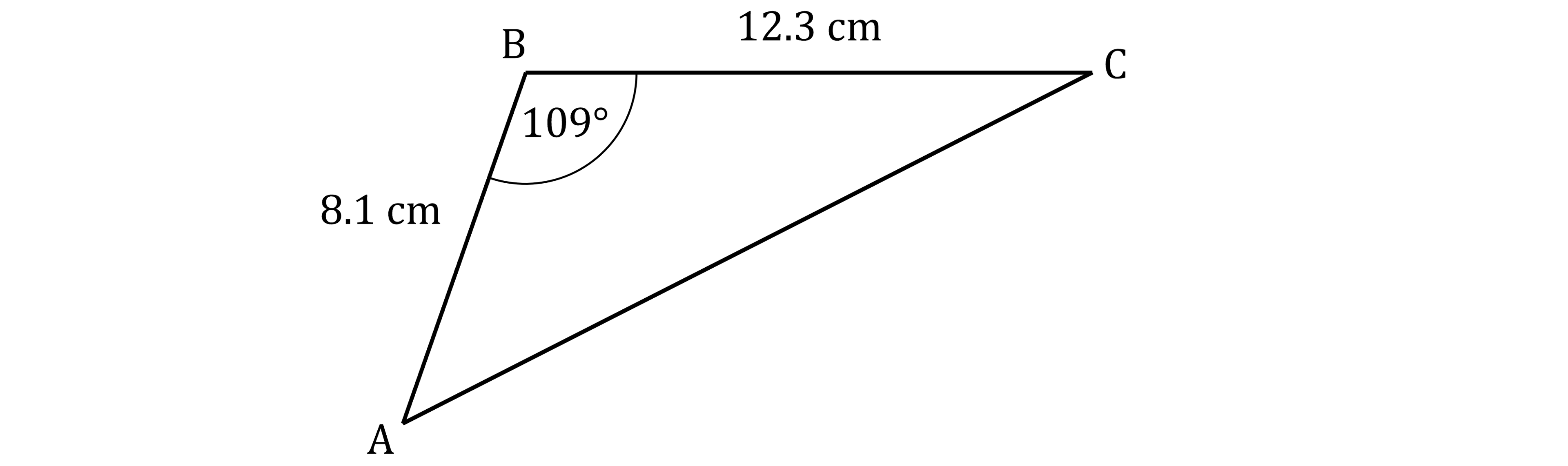
Triangle ABC with AB = 8.1 cm, BC = 12.3 cm, and angle ABC = 109º.

  • Angle ABC = 109°

  • AB = 8.1 cm

  • BC = 12.3 cm

Calculate the area of the triangle.

Answer:

Label the sides of the triangle

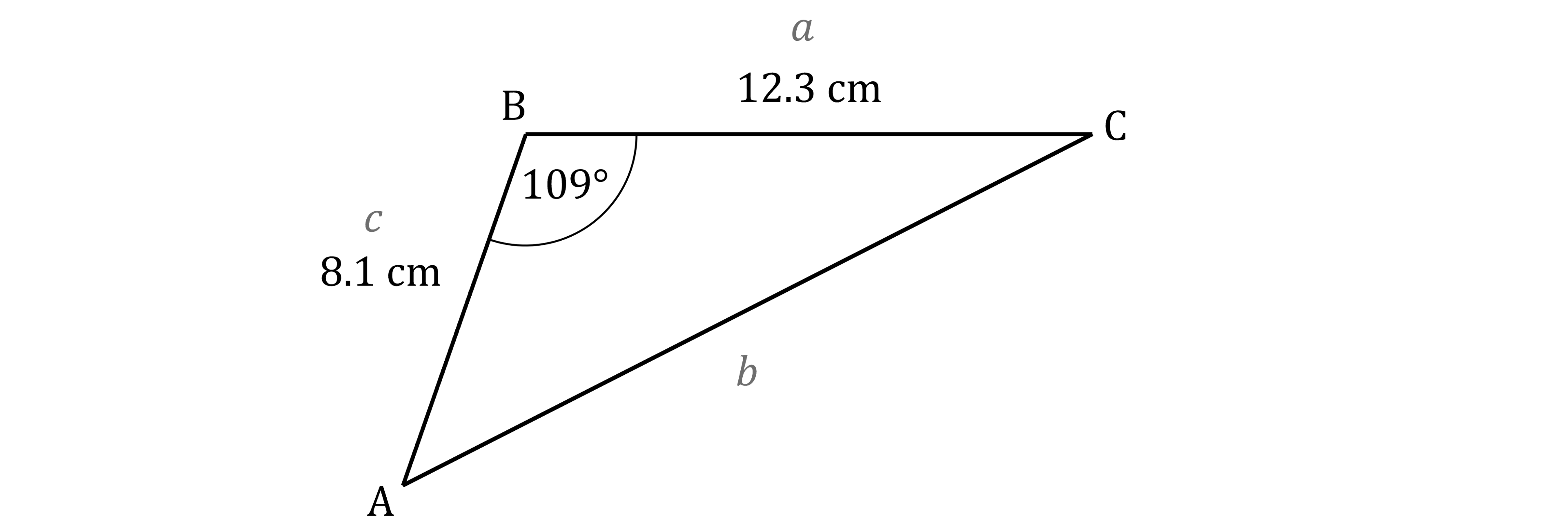
Triangle ABC with sides opposite angles labelled with corresponding lowercase letters.

You want to find the area and are given the size of angle B

  • So swap the letters around in the Formulae List form of the triangle area formula to get space Area equals 1 half a c sin B space

Substitute the known values into that equation

table row cell space Area end cell equals cell 1 half cross times 8.1 cross times 12.3 cross times sin open parentheses 109 close parentheses end cell row blank equals cell 47.101007... end cell end table

Round to a sensible degree of accuracy

  • Unless a question tells you otherwise, 3 significant figures is usually a good choice

47.1 cm2  (3 s.f.)

Using the area of a triangle to find a length or angle

How do I find a length or angle when I know the area of a non-right-angled triangle?

  • You may be given the area of a non-right-angled triangle

    • and asked to find a side length or an angle

  • To do this

    • Substitute the information you do know into the triangle area formula Area equals 1 half a b sin C space

    • Then rearrange the formula to make the thing you are looking for the subject

  • For example, to find the length of side a

    • the formula rearranges to space a equals fraction numerator 2 cross times Area over denominator b sin C space end fraction

  • Or to find the angle C

    • the formula rearranges to space sin C space equals fraction numerator 2 cross times Area over denominator a b end fraction

    • Then use the cos-1 feature on your calculator to find C

Worked Example

In the diagram

  • Angle BAC = 26°

  • AC = 30 cm

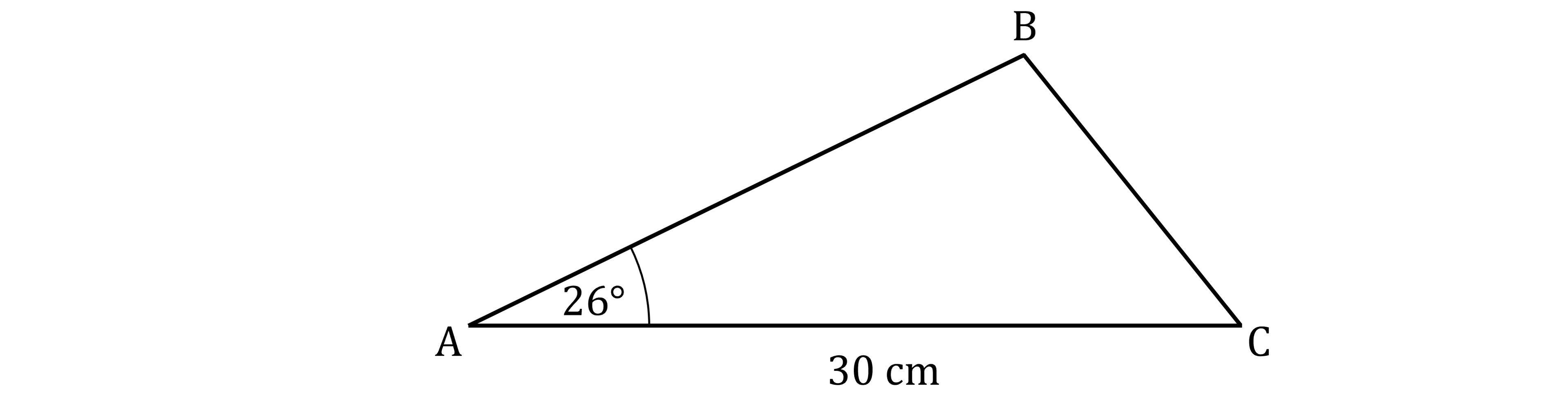
Triangle ABC, angle A is 26°, side AC measures 30 cm.

The area of triangle ABC is 160 square centimetres.

Calculate the length of AB.

Answer:

Label the sides of the triangle

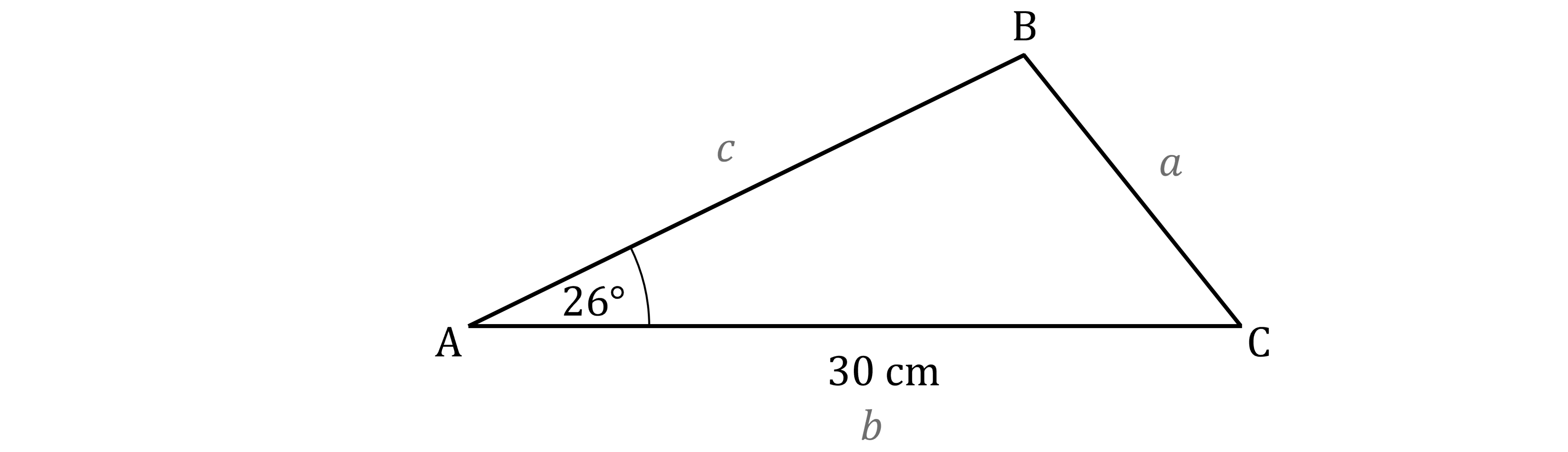
Triangle ABC with sides opposite angles labelled with corresponding lowercase letters.

You want to find the length of c, and you know the area, the length of b and the angle at A

  • So swap the letters around in the Formulae List form of the triangle area formula to get space Area equals 1 half b c sin A space

Substitute the known values into that equation

table row cell space 160 end cell equals cell 1 half cross times 30 cross times c cross times sin open parentheses 26 close parentheses end cell end table

Rearrange to make c the subject

table row c equals cell fraction numerator open parentheses 2 cross times 160 close parentheses over denominator 30 cross times sin open parentheses 26 close parentheses end fraction end cell row blank equals cell 24.332501... end cell end table

Round to a sensible degree of accuracy

  • Unless a question tells you otherwise, 3 significant figures is usually a good choice

24.3 cm  (3 s.f.)

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Cosine RuleNext:Bearings
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.