National 5MathsSQARevision NotesTrigonometric SkillsTrigonometry with TrianglesBearings

Bearings (SQA National 5 Maths): Revision Note

Exam code: X847 75

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

Bearing basics

What are bearings?

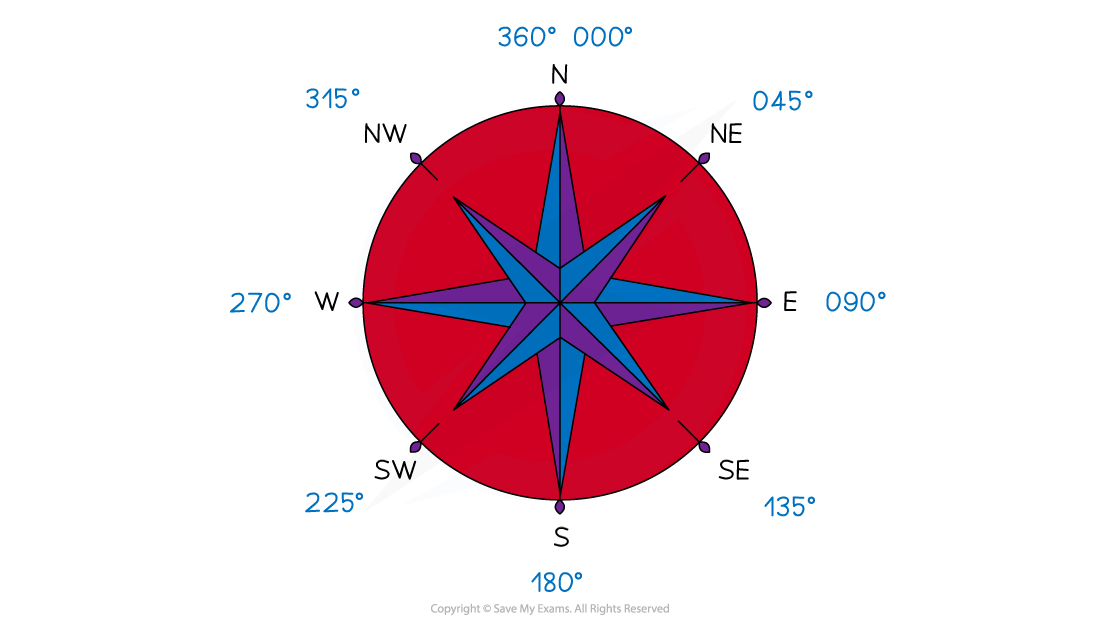
  • Bearings are a way of describing an angle

    • They are commonly used in navigation

  • There are three rules which must be followed when using a bearing:

    1. They are measured from North

      • North is usually straight up on a scale drawing or map, and should be labelled on the diagram

    2. They are measured clockwise

    3. The angle should always be written with 3 digits

      • 059° instead of just 59°

  • Knowing the compass directions and their respective bearings can be helpful 

Compass direction bearings

How do I find a bearing between two points?

  • Identify where you need to start

    • "The bearing of A from B" means start at B and find the bearing to A

    • "The bearing of B from A" means start at A and find the bearing to B

  • Draw a North line at the starting point

  • Draw a line between the two points

  • Measure the angle between the North line and the line joining the points

    • Measure clockwise from North

  • Write the angle using 3 figures 

How do I find the bearing of B from A if I know the bearing of A from B?

  • If the bearing of A from B is less than 180°

    • Add 180° to it to find the bearing of B from A

  • If the bearing of A from B is more than 180°

    • Subtract 180° from it to find the bearing of B from A

Using bearings with trigonometry

How do I answer trickier questions involving bearings?

  • A bearings question is usually a set-up for a question about trigonometry

  • Answering the question may involve:

  • You may need to find missing distances (lengths) and directions (angles) before you are able to find a particular bearing

Examiner Tips and Tricks

A diagram is an essential part of answering a bearings question. Draw one if one is not provided, or add information to one that is provided with the question.

Worked Example

In the diagram A, B and C represent the positions of three ships.

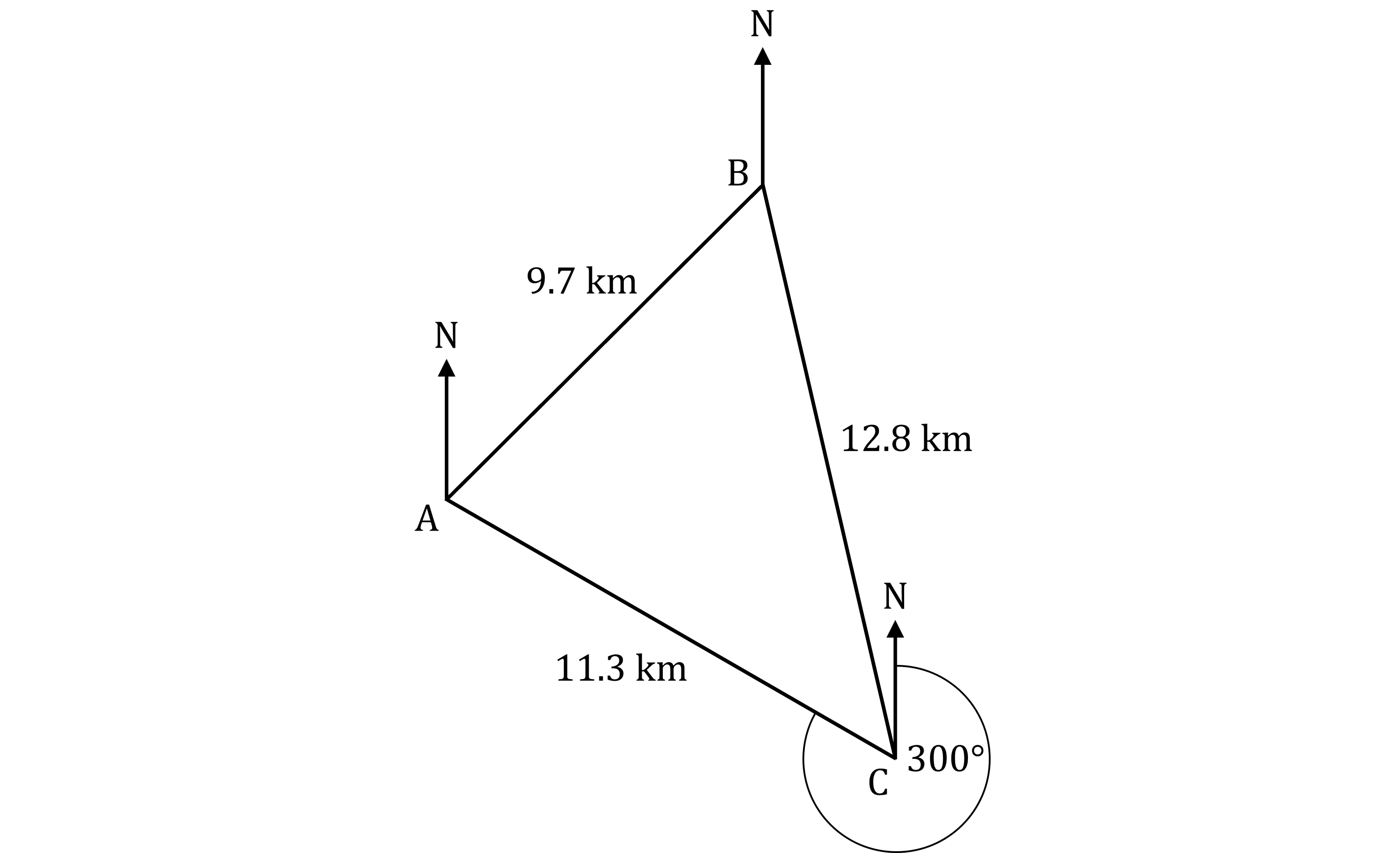
Triangle ABC has sides AB 8.4 km, BC 12.8 km, CA 11.3 km. North arrows at each vertex, and a 300-degree angle marked at C from the north arrow clockwise to AC.

  • AB is 9.7 km.

  • BC is 12.8 km.

  • AC is 11.3 km.

  • The bearing of A from C is 300°.

Calculate the bearing of B from C.

Do not use a scale drawing.

Answer:

"Do not use a scale drawing" means you need to work out the necessary angle using trigonometry, and not just try to measure angles on the diagram

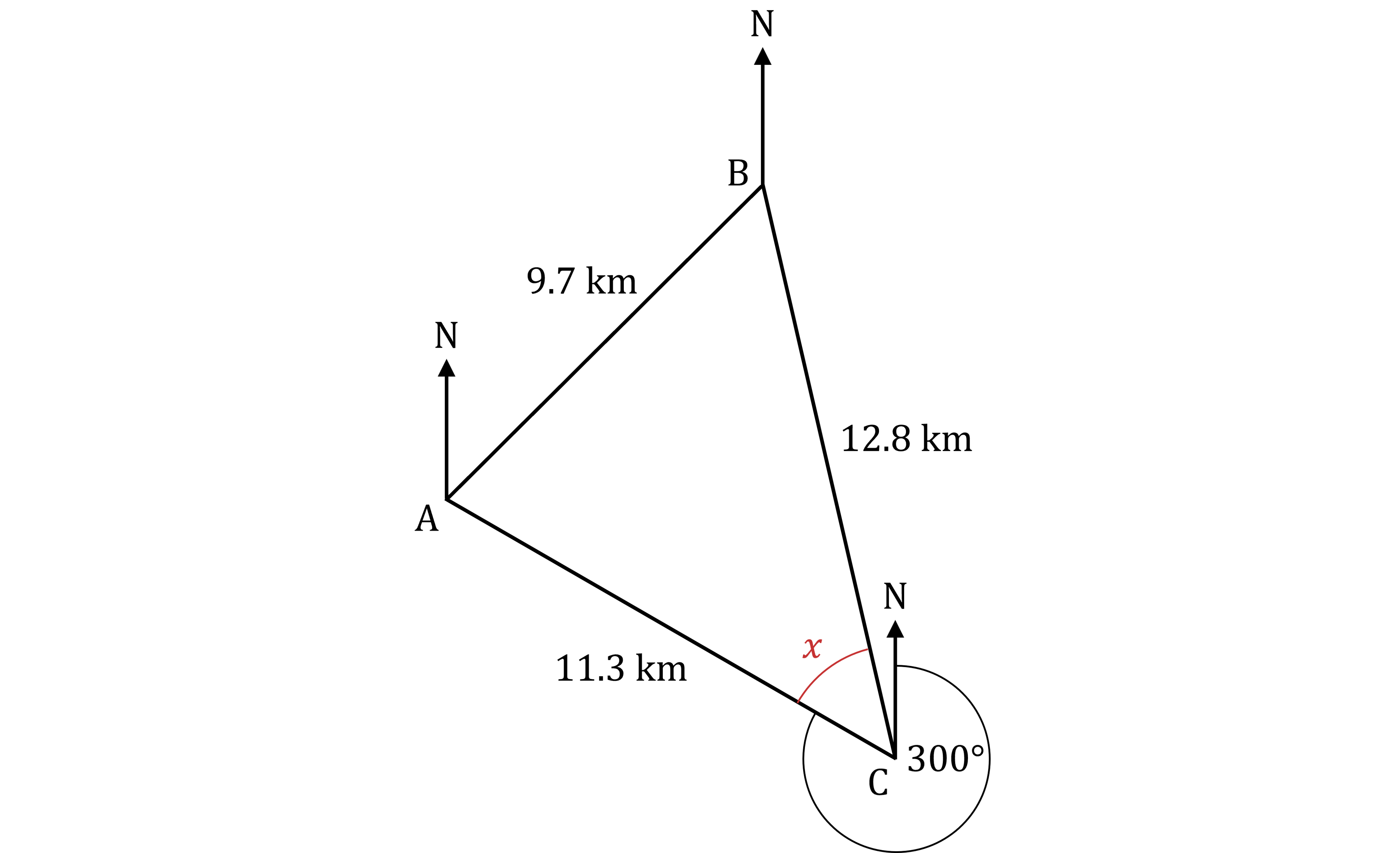
The bearing you are looking for is the angle from the North line at C, all the way around clockwise to line segment BC

To find this bearing you can

  • find the angle marked x in the diagram below

  • and then add that to 300°

On the diagram from the question, angle ACB has been marked and labelled x.

Here you know 3 sides in a triangle, and want to know an angle

  • This means you can use the Cosine Rule

Label the sides of the triangle

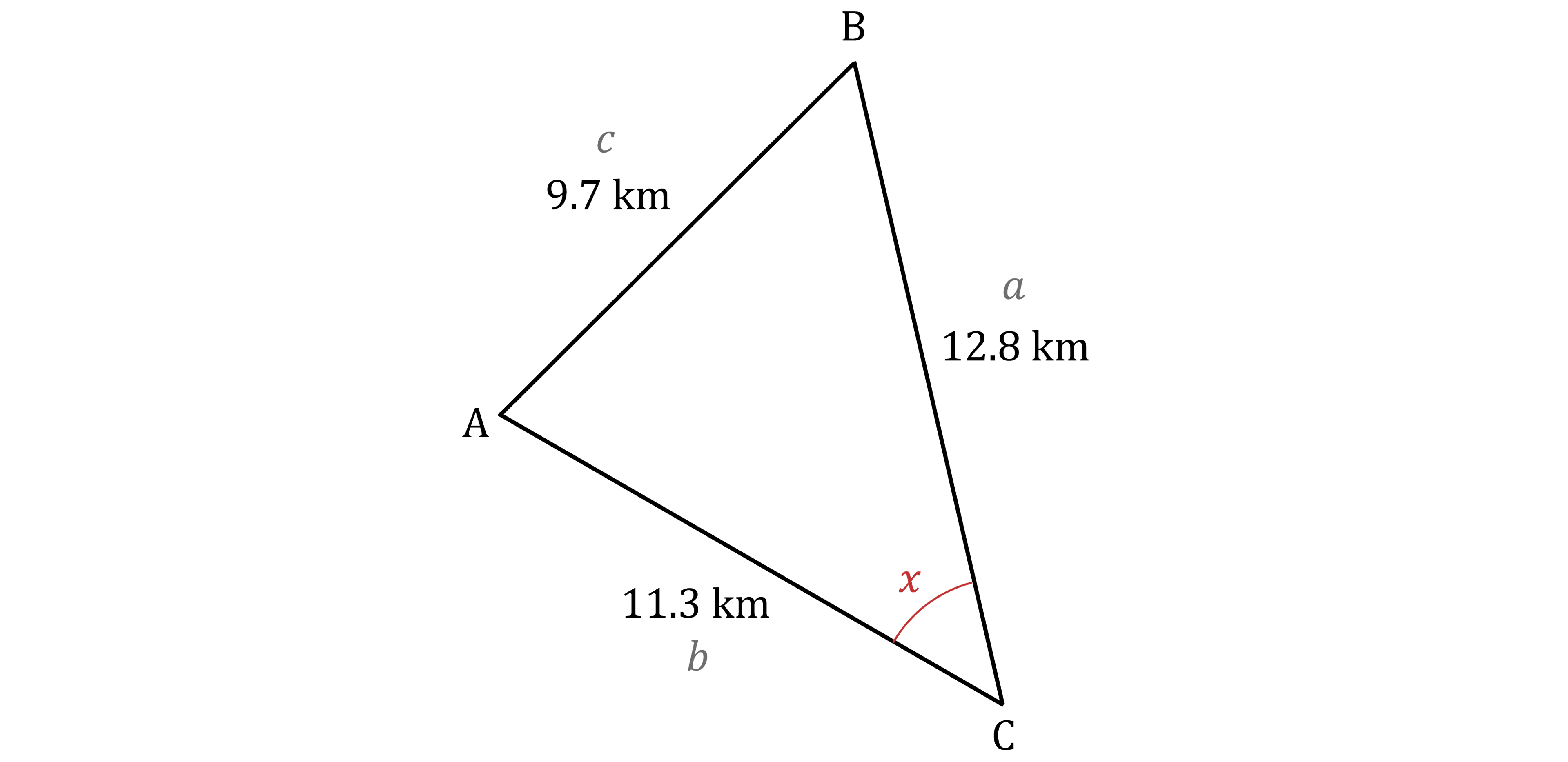
Triangle with vertices A, B, C; sides AB 8.4 km, BC 12.8 km, AC 11.3 km. Angle at C marked as x, sides labelled a, b, c.

You want to find the size of the angle at C

  • So use the Cosine Rule equation cos A equals fraction numerator b squared plus c squared minus a squared over denominator 2 b c end fraction from the Formulae List

  • But swap the letters around to get it in the form space cos C equals fraction numerator a squared plus b squared minus c squared over denominator 2 a b end fraction

Substitute the known values into that equation

cos x equals fraction numerator 11.3 squared plus 12.8 squared minus 9.7 squared over denominator 2 cross times 11.3 cross times 12.8 end fraction

Use cos-1 on your calculator to find the value of x

table row x equals cell cos to the power of negative 1 end exponent open parentheses fraction numerator 11.3 squared plus 12.8 squared minus 9.7 squared over denominator 2 cross times 11.3 cross times 12.8 end fraction close parentheses end cell row blank equals cell 46.958953... end cell end table

So the bearing of B from C is

300 plus table row blank blank 46 end table table row blank blank. end table table row blank blank 958953 end table table row blank blank. end table table row blank blank. end table table row blank blank. end table table row blank equals blank end table table row blank blank 346 end table table row blank blank. end table table row blank blank 958953 end table table row blank blank. end table table row blank blank. end table table row blank blank. end table

Round to a sensible degree of accuracy

  • Unless a question tells you otherwise, to the nearest degree is usually a good choice for bearings

347°  (to the nearest degree)

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Area of a TriangleNext:Problem-Solving with Triangles
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths Content Creator

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.